ベクトルが表す点の存在範囲
$\triangle OAB$ において,$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ で表されるときの点 $P$ の存在範囲は
1 $s+t=1 \iff$ 点 $P$ は直線 $AB$ 上
2 $s≧0,t≧0,s+t=1 \iff$ 点 $P$ は線分 $AB$ 上
3 $s≧0,t≧0,s+t≦1 \iff$ 点 $P$ は $\triangle OAB$ の周および内部
4 $0≦s≦1,0≦t≦1 \iff$ 点 $P$ は平行四辺形 $OACB$ の周および内部
ただし,点 $C$ は $\overrightarrow{OA}=\overrightarrow{BC}$ を満たす点
1 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s+t=1$
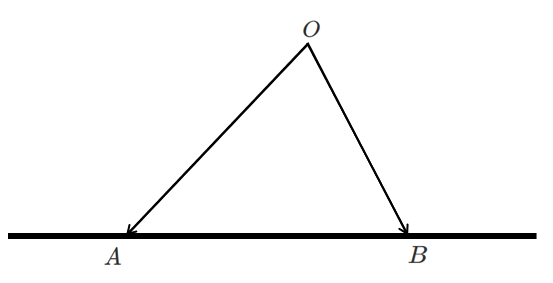
点 $P$ は直線 $AB$ 上
2 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s≧0,t≧0,s+t=1$
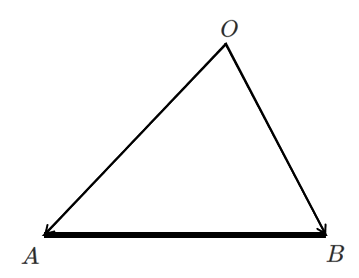
点 $P$ は線分 $AB$ 上
3 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s≧0,t≧0,s+t≦1$
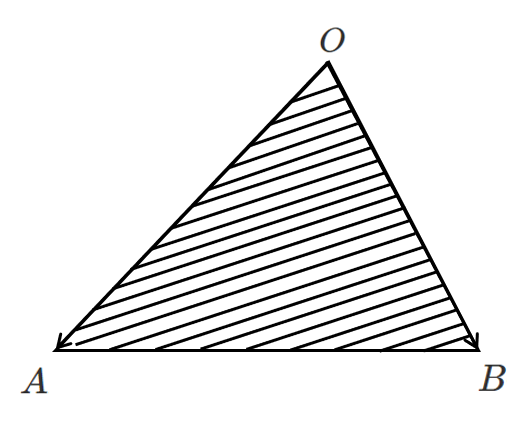
点 $P$ は$\triangle OAB$ の周および内部
4 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $0≦s≦1,0≦t≦1$
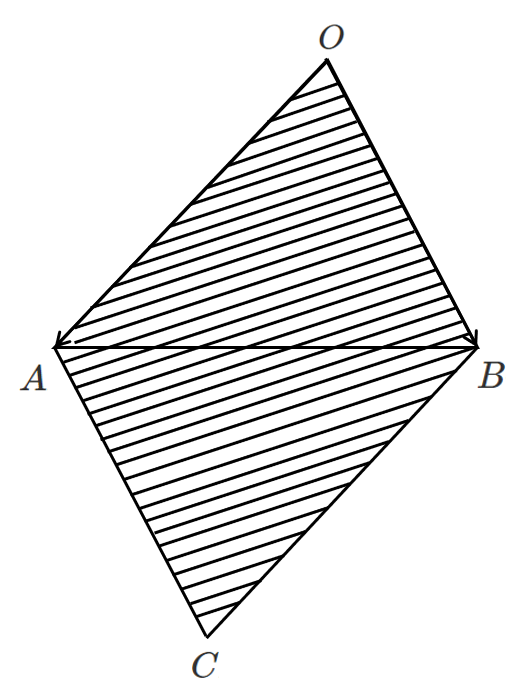
点 $P$ は平行四辺形 $OACB$ の周および内部
ただし,点 $C$ は $\overrightarrow{OA}=\overrightarrow{BC}$ を満たす点

今回は1と2の存在範囲について考えてみよう!
直線 $AB$ 上の場合
1 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s+t=1$

点 $P$ は直線 $AB$ 上

これは「内分点と外分点におけるベクトル」を考えれば理解できるよ!
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s+t=1$
を簡単にすると
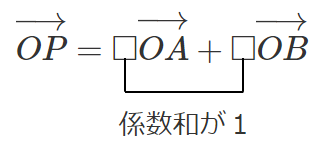
内分点におけるベクトルを考えてみると
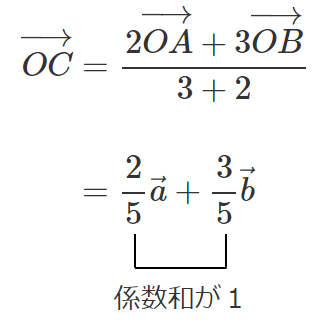
外分点におけるベクトルを考えてみると


たしかに,内分点と外分点におけるベクトルは「係数和が1」になるね!

文字式でも確認しておこう!
● 内分点におけるベクトル
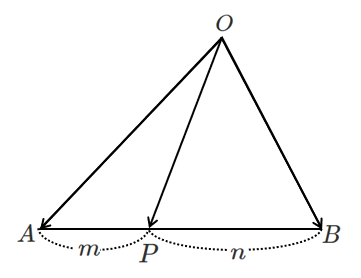
● 外分点におけるベクトル
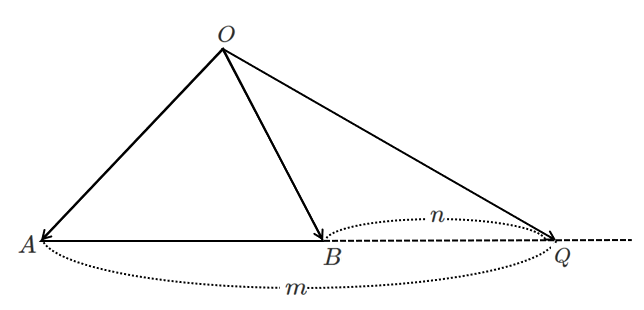
$m>n$ のとき
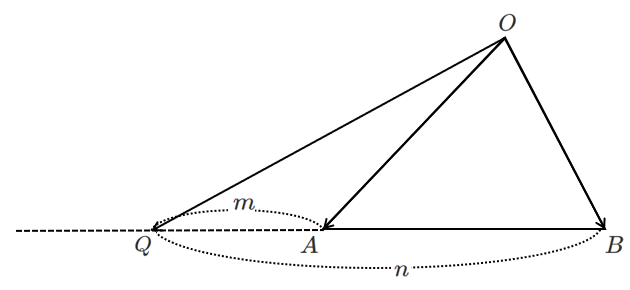
$m<n$ のとき
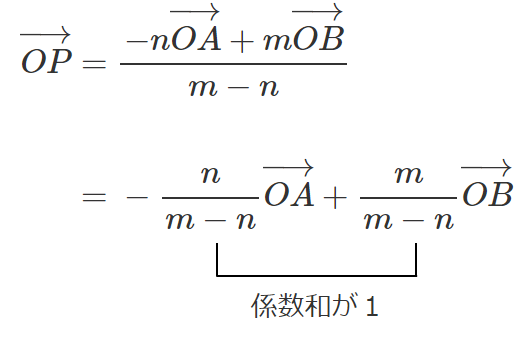
以上より
内分点と外分点におけるベクトルは「係数和が1」になる
つまり
点 $P$ が辺 $AB$ の内分点または外分点の場合は 「係数和が1」になる
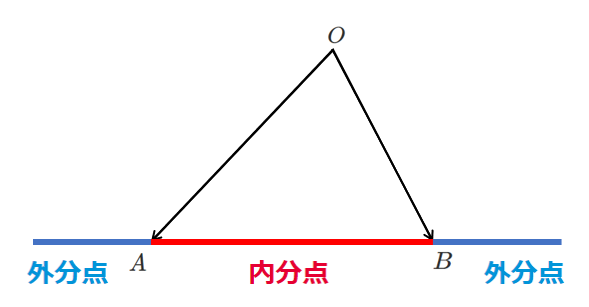
$s=1,t=0$ のとき
$\overrightarrow{OP}=\overrightarrow{OA}$
点 $P$ は点 $A$ と一致する
$s=0,t=1$ のとき
$\overrightarrow{OP}=\overrightarrow{OB}$
点 $P$ は点 $B$ と一致する
よって
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s+t=1$
のとき

点 $P$ は直線 $AB$ 上
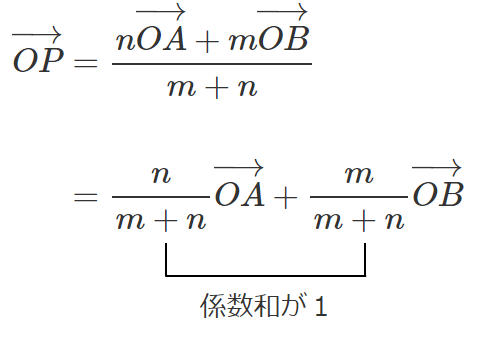
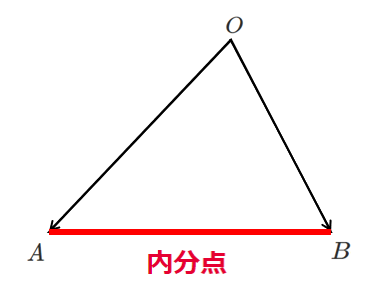
線分 $AB$ 上の場合
2 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s≧0,t≧0,s+t=1$

点 $P$ は線分 $AB$ 上
1 $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s+t=1$
の条件に
$s≧0,t≧0$
「係数がともに $0$ 以上」という条件が加わったと考えればよい
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s≧0,t≧0,s+t=1$
を簡単にすると
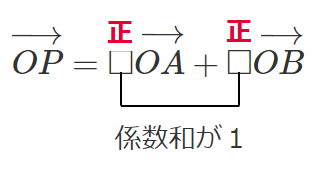
正確には係数が $0$ 以上
内分点におけるベクトルの場合は
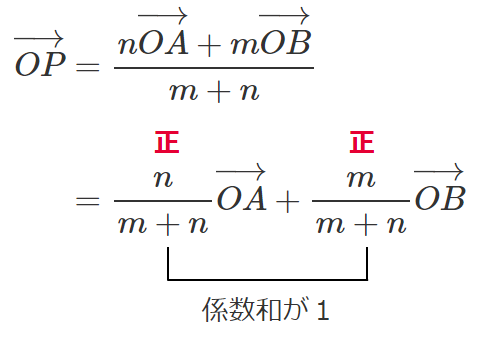
「係数がともに正」になる
外分点におけるベクトルの場合は
$m>n$ のとき
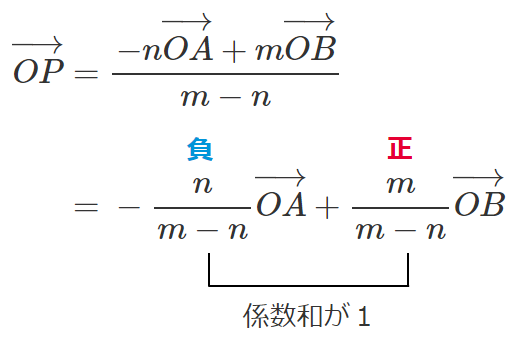
$m<n$ のとき
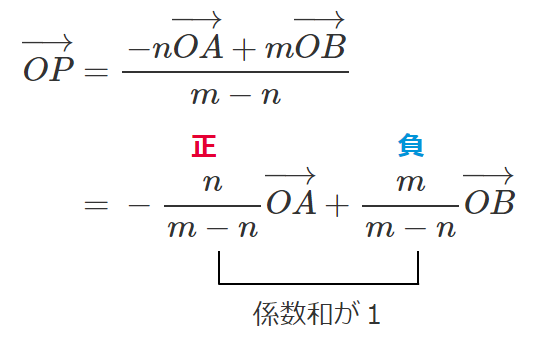
「係数のどちらかが負」になる
よって
点 $P$ が辺 $AB$ の内分点の場合「係数和が1」かつ「係数がともに正」である
$s=1,t=0$ のとき
$\overrightarrow{OP}=\overrightarrow{OA}
点 $P$ は点 $A$ と一致する
$s=0,t=1$ のとき
$\overrightarrow{OP}=\overrightarrow{OB}
点 $P$ は点 $B$ と一致する
したがって
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s≧0,t≧0,s+t=1$
のとき

点 $P$ は線分 $AB$ 上
存在範囲の利用
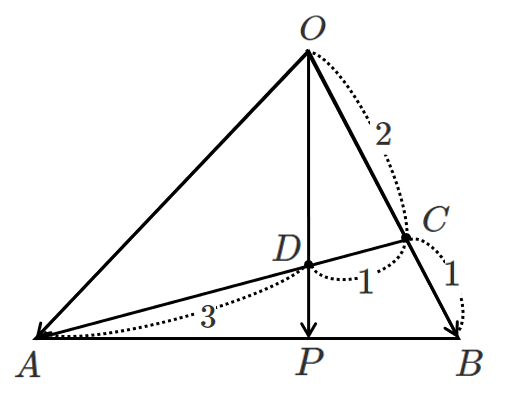
辺 $OB$ を $2:1$ に内分した点を $C$ なので
$\displaystyle{\overrightarrow{OC}=\frac{2}{3}\overrightarrow{OB}}$
線分 $AC$ を $3:1$ に内分した点を $D$ なので
\begin{eqnarray} \overrightarrow{OD} &=& \frac{\overrightarrow{OA}+3\overrightarrow{OC}}{3+1} \\\\ &=& \frac{\overrightarrow{OA}+3\cdot\frac{2}{3}\overrightarrow{OB}}{3+1} \\\\ &=& \frac{1}{4}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB} \end{eqnarray}直線 $OD$ 上に点 $P$ があるので,
$\overrightarrow{OP}=k\overrightarrow{OD}$($k$ は実数)
と表せる
\begin{eqnarray} \overrightarrow{OP} &=& k(\frac{1}{4}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}) \\\\ &=& \frac{1}{4}k\overrightarrow{OA}+\frac{1}{2}k\overrightarrow{OB} \end{eqnarray}点 $P$ は直線 $AB$ 上にあるので

したがって
$\displaystyle{\overrightarrow{OP}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}}$

問題にも使えるから,知っておくと便利だね!
まとめ
● $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s+t=1$


点 $P$ は直線 $AB$ 上
● $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ $s≧0,t≧0,s+t=1$

正確には係数が $0$ 以上

点 $P$ は線分 $AB$ 上

問題で使えるように理解を深めておこう!




コメント