ベクトルの内積
$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
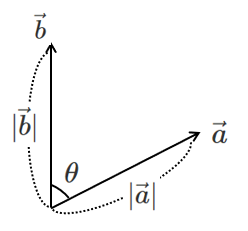
なす角 $\theta$ は「始点を合わせたときの角度」のこと
また,$0^\circ≦\theta≦180^\circ$

内積の意味が知りたい場合はこれ↓

内積の計算

内積を求める練習をしよう!
下の図の直角三角形において,次の内積を求めよ。
(1) $\overrightarrow{AB}\cdot\overrightarrow{AC}$
(2) $\overrightarrow{BA}\cdot\overrightarrow{CB}$
(3) $\overrightarrow{CA}\cdot\overrightarrow{BC}$
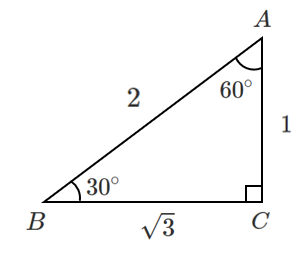
(1) $\overrightarrow{AB}\cdot\overrightarrow{AC}$
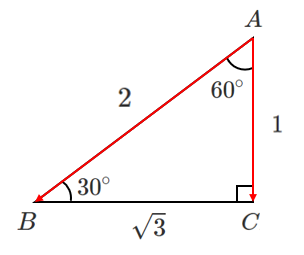
(2) $\overrightarrow{BA}\cdot\overrightarrow{CB}$
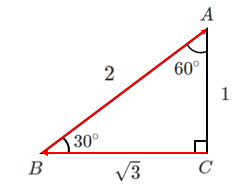
始点をそろえるために $\overrightarrow{CB}$ を平行移動すると
なす角は $150^\circ$ となる
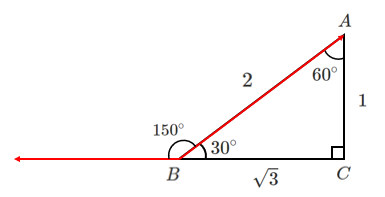
(3) $\overrightarrow{CA}\cdot\overrightarrow{BC}$
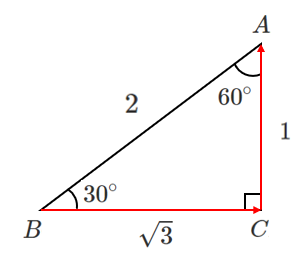
始点をそろえるために $\overrightarrow{BC}$ を平行移動すると
なす角は $90^\circ$ となる
\begin{eqnarray} \overrightarrow{CA}\cdot\overrightarrow{BC} &=& |\overrightarrow{CA}||\overrightarrow{BC}|\cos90^\circ \\ &=& 1\cdot\sqrt{3}\cdot0 \\ &=& 0 \end{eqnarray}

始点をそろえて,なす角を求めることが重要だね!
成分表示における内積
成分表示の復習はこれ↓

$\triangle OAB$ において,$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OB}=\vec{b}$ とする
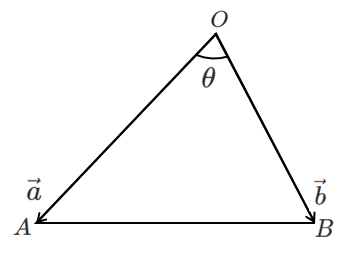
余弦定理を用いると,
$BA^2=OA^2+OB^2-2\cdot OA\cdot OB\cos\theta$
$\overrightarrow{BA}=\vec{a}-\vec{b}$ より(ベクトルの減法)
$|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos\theta$
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$ より
$|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2\vec{a}\cdot\vec{b}$ $\cdots$ ①
ここで,$\vec{a}=(a_1,a_2)$,$\vec{b}=(b_1,b_2)$ とすると
$\vec{a}-\vec{b}=(a_1-b_1,a_2-b_2)$ なので,
$|\vec{a}|=\sqrt{a_1^2+a_2^2}$
$|\vec{b}|=\sqrt{b_1^2+b_2^2}$
$|\vec{a}-\vec{b}|=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$
①より
$(a_1-b_1)^2+(a_2-b_2)^2=(a_1^2+a_2^2)+(b_1^2+b_2^2)-2\vec{a}\cdot\vec{b}$
これを整理すると
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$
$\vec{a}=(a_1,a_2)$,$\vec{b}=(b_1,b_2)$ のとき
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$

成分表示における内積は,$x$ 成分同士と $y$ 成分同士をそれぞれかけて足すだけ!
ベクトルのなす角
ベクトルのなす角を求めたいとき,内積の式
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

を使うことができる
なす角 $\theta$ を求めるので,この式を変形して
$\displaystyle{\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}}$
の形で用いた方がよい
ただし, $0^\circ≦\theta≦180^\circ$
$\displaystyle{\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}}$

この式を使って,なす角を求めてみよう!
$\vec{a}\cdot\vec{b}=2\cdot(-3)+1\cdot1=-5$
$|\vec{a}|=\sqrt{2^2+1^2}=\sqrt{5}$
$|\vec{b}|=\sqrt{(-3)^2+1^2}=\sqrt{10}$
よって
$\displaystyle{\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=\frac{-5}{\sqrt{5}\sqrt{10}}=-\frac{1}{\sqrt{2}}}$
$0^\circ≦\theta≦180^\circ$ なので
$\theta=135^\circ$

$\vec{a}\cdot\vec{b}$ と $|\vec{a}|$ と $|\vec{b}|$ が求まれば,なす角を求めることができるね!
垂直条件

垂直条件は出題される可能性が極めて高い!
理解して使えるようにしよう!
$\vec{0}$ でない2つのベクトル $\vec{a}$ と $\vec{b}$ のなす角が $90^\circ$ のとき
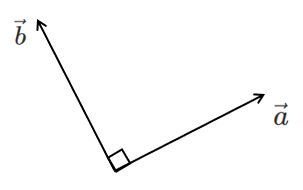
$\vec{a}$ と $\vec{b}$ は垂直であるといい
$\vec{a}\perp\vec{b}$
とかく
$\vec{a}\perp\vec{b}$ のとき,内積 $\vec{a}\cdot\vec{b}$ を計算すると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos90^\circ$
$\cos90^\circ=0$ なので,$|\vec{a}|$ と $|\vec{b}|$ がどのような値でも
$\vec{a}\cdot\vec{b}=0$
が成り立つ
逆に, $\vec{0}$ でない2つのベクトル $\vec{a}$ と $\vec{b}$ について
$\vec{a}\cdot\vec{b}=0$
となるのは, $\vec{a}\perp\vec{b}$ のときである
$\vec{a}≠\vec{0}$,$\vec{b}≠\vec{0}$ のとき
$\vec{a}\perp\vec{b} \iff \vec{a}\cdot\vec{b}=0$

ベクトルの問題で「垂直」を表すキーワードが出たら,「内積が $0$」と思いつくようにしよう!
$\vec{a}\perp\vec{b}$ より,$\vec{a}\cdot\vec{b}=0$
$2x+3\cdot4=0$
$x=-6$
まとめ
● ベクトルの内積
$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
ただし,$0^\circ≦\theta≦180^\circ$
● 成分表示における内積
$\vec{a}=(a_1,a_2)$,$\vec{b}=(b_1,b_2)$ のとき
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$
● ベクトルのなす角を求める式
内積の式を変形した式
$\displaystyle{\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}}$
● ベクトルの垂直条件
$\vec{a}≠\vec{0}$,$\vec{b}≠\vec{0}$ のとき
$\vec{a}\perp\vec{b} \iff \vec{a}\cdot\vec{b}=0$

内積はベクトルの問題を解くうえで超重要!
しっかりおさえておこう!




コメント