実数倍のベクトル

あるベクトル $\vec{a}$ に対して,$k\vec{a}$($k$ は定数)を考えてみよう!
$\vec{a}$ を実数倍する
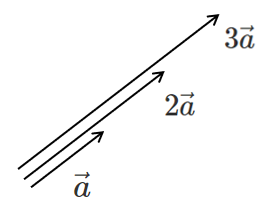
$2\vec{a}$ や $3\vec{a}$ は
$-\vec{a}$ や $-2\vec{a}$ や $-3\vec{a}$ は
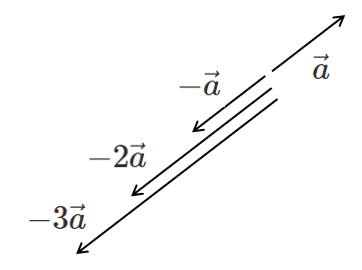

マイナスがついたら向きが逆になるね!
平行なベクトル
$\vec{a}\parallel\vec{b}$ のとき
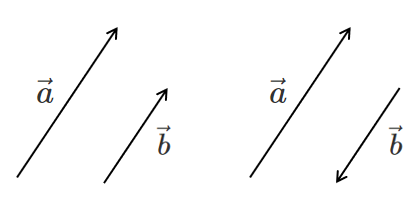
向きが逆向きでも平行という

単位ベクトルは「大きさが $1$ のベクトル」!
$|\vec{a}|=2$ である $\vec{a}$ と平行な単位ベクトル(大きさが $1$ のベクトル)
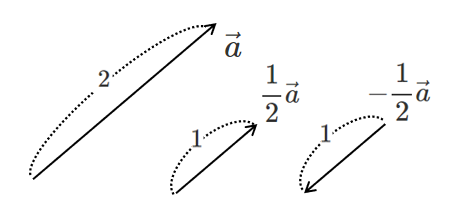
$\displaystyle{\frac{1}{2}\vec{a}}$, $\displaystyle{-\frac{1}{2}\vec{a}}$
ベクトルの分解
ベクトルの加法
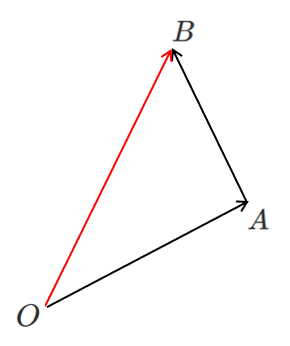
$\overrightarrow{OA}+ \overrightarrow{AB}= \overrightarrow{OB}$
を利用して
あるベクトルを和の形に分解することを「ベクトルの分解」という
例えば,
$\overrightarrow{AB}$ について「ベクトルの分解」をすると
$\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}$
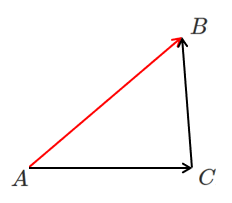
$\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB}$
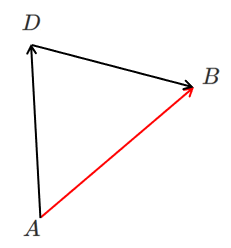
以上のように「ベクトルの分解」ができる

「ベクトルの分解」を用いて問題を解いてみよう!
正六角形 $ABCDEF$ において,$\overrightarrow{AB}=\vec{a}$,$\overrightarrow{AF}=\vec{b}$ とする。
次のベクトルを $\vec{a}$,$\vec{b}$ を用いて表せ。
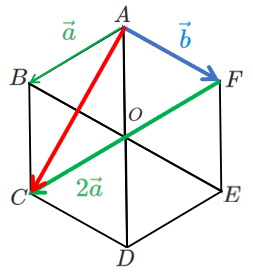
(1) $\overrightarrow{AC}$
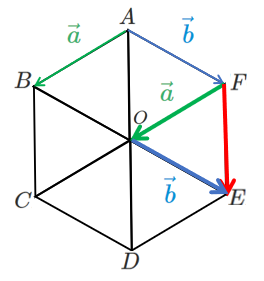
(2) $\overrightarrow{FE}$
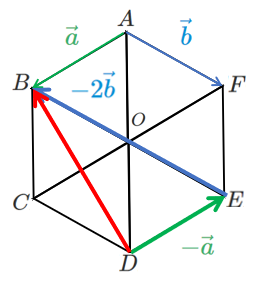
(3) $\overrightarrow{DB}$
(1) $\overrightarrow{AC}$
(2) $\overrightarrow{FE}$
(3) $\overrightarrow{DB}$

この問題が解けたら,「ベクトルの分解」は完璧!
まとめ
● ベクトルの実数倍

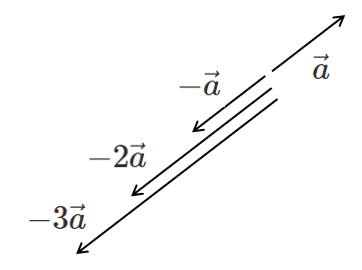
マイナスがついたら向きは逆になる
● 平行なベクトル
$\vec{a} \parallel \vec{b}$ のとき
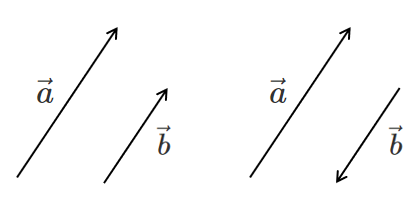
● ベクトルの分解
例 $\overrightarrow{AB}$
$\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}$

$\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB}$


ベクトルの分解は使う場面が多いので慣れておこう!




コメント