不定積分

原始関数

$x$ で微分すると $f(x)$ になる関数を，$f(x)$ の　原始関数　という

つまり

$F'(x)=f(x)$ のとき，$F(x)$ は $f(x)$ の原始関数である

図で表すと以下のようになる

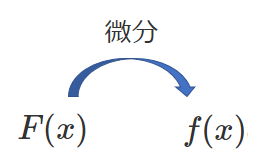
$F(x)$ は $f(x)$ の原始関数

　微分して $2x$ になる関数は

①　$x^2$　　と　　④　$x^2+1$

不定積分

積分定数とは

例　$2x$ の原始関数

$x^2$，$x^2+1$，$x^2+2$，$x^2-1$，……

したがって

$f(x)$ の任意の原始関数は「$F(x)+$ 定数」の形に表される

この定数を　積分定数　といい，記号 $C$ で表すと

$f(x)$ の任意の原始関数は「$F(x)+C$」と表される

不定積分とは

「$F(x)+C$ ($C$ は積分定数)」を $f(x)$ の　不定積分　という

例　$2x$ の不定積分

$x^2+C$　　ただし，$C$ は積分定数

積分するとは

関数 $f(x)$ の不定積分を求めることを，$f(x)$ を　積分する　という

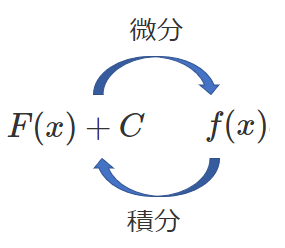
$f(x)$ を積分する（不定積分を求める）ことを記号で表すと

$\displaystyle{\int f(x)dx}$

よって，不定積分は以下のような式で表せる

$\displaystyle{\int}$ の使い方は

$\displaystyle{\int}$ (積分する関数) $dx$

のように，積分したい関数を　 $\displaystyle{\int}$　と　$dx$　の間に入れる

関数 $x^n$ の不定積分

(1)　$\displaystyle{\int 1 dx=x+C}$　　　$C$ は積分定数

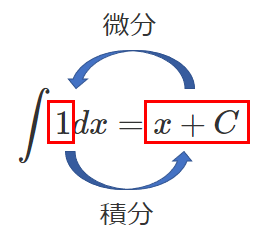
(2)　$\displaystyle{\int x dx=\frac{1}{2}x^2+C}$　　　$C$ は積分定数

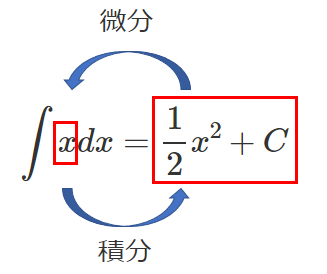
(3)　$\displaystyle{\int x^2 dx=\frac{1}{3}x^3+C}$　　　$C$ は積分定数

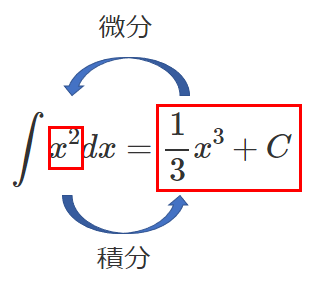
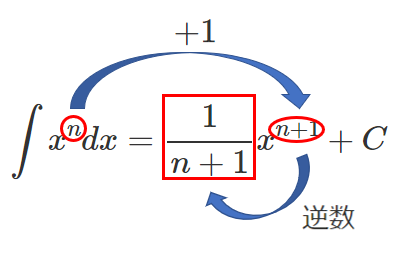
一般に次の公式が成り立つ

関数の定数倍および和，差の不定積分

１　$\displaystyle{\int kf(x) dx=kF(x)+C}$　 　$k$ は定数

例　$\displaystyle{\int 3x dx=3\cdot\frac{1}{2}x^2+C=\frac{3}{2}x^2+C}$

２　$\displaystyle{\int \{f(x)+g(x)\} dx=F(x)+G(x)+C}$

例　$\displaystyle{\int (x^2+x) dx=\frac{1}{3}x^3+\frac{1}{2}x^2+C}$

３　$\displaystyle{\int \{f(x)-g(x)\} dx=F(x)-G(x)+C}$

例　$\displaystyle{\int (x^2-x) dx=\frac{1}{3}x^3-\frac{1}{2}x^2+C}$

問題

(1)　$\displaystyle{\int (3x+2) dx}$

$\displaystyle{\int (3x+2) dx=3\cdot\frac{1}{2}x^2+2x+C=\frac{3}{2}x^2+2x+C}$

(2)　$\displaystyle{\int (6x^2+2x-1) dx}$

$\displaystyle{\int (6x^2+2x-1) dx=6\cdot\frac{1}{3}x^3+2\cdot\frac{1}{2}x^2-x+C=2x^3+x^2-x+C}$

まとめ

● 関数 $f(x)$ の不定積分

　$F'(x)=f(x)$ のとき

　　$\displaystyle{\int f(x)dx=F(x)+C}$　　ただし，$C$ は積分定

● 関数 $x^n$ の不定積分

　$\displaystyle{\int x^n dx=\frac{1}{n+1}x^{n+1}+C}$　　$C$ は積分定数