同一平面上にある点

点と平面

　$3$ 点を通る平面は１つだけ

$2$ 点を通る平面は１つに定まらない

指先を点，下敷きを平面だと考えよう！

指を３本立てて，その上に下敷きを乗せてみて！

３本の指の上に乗ったよ！

指２本で同じことをするとどうなる？

下敷きがぐらぐらして安定しない！

このことから，$3$ 点を通る平面は１つだけど，$2$ 点を通る平面は１つではないことが分かるね！

$3$ 点でつくられる平面上にある点

　平面 $ABC$ 上に点 $P$ があるとき

$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$

　を満たす実数 $s$，$t$ が存在する

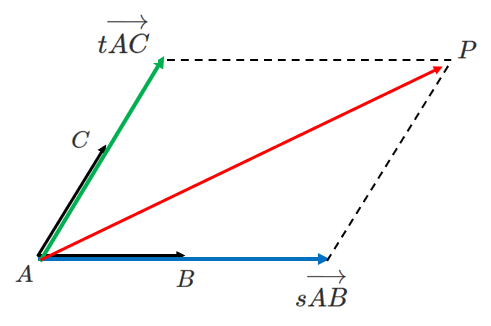
$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$

平面 $ABC$ における点 $A$ を始点とする $\overrightarrow{AB}$，$\overrightarrow{AC}$ を用いると

同じ平面上にある点 $P$ について，$\overrightarrow{AP}$ は

$\overrightarrow{AP}=□\overrightarrow{AB}+□\overrightarrow{AC}$

と１通りに表すことができる

始点を $B$ や $C$ にしてもよい

例えば

$\overrightarrow{CP}=s\overrightarrow{CA}+t\overrightarrow{CB}$

のように表すことができる

　$A(2，0，-1)$，$B(1，2，0)$，$C(0，1，-2)$ を通る平面 $ABC$ 上に点 $P(3，1，z)$ があるとき，$z$ の値を求めよ。

　平面 $ABC$ 上に点 $P$ があるので

$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$

　となる実数 $s$，$t$ が存在する

$\overrightarrow{AB}=(-1，2，1)$

$\overrightarrow{AC}=(-2，1，-1)$

$\overrightarrow{AP}=(1，1，z+1)$

　$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$ より

\begin{eqnarray} (1，1，z+1) &=& s(-1，2，1)+t(-2，1，-1) \\\\ &=& (-s-2t，2s+t，s-t) \end{eqnarray}

\[ \left\{ \begin{array}{l} 　-s-2t &=& 1　　　　\cdots\cdots　① \\ 　2s+t &=& 1　　　　\cdots\cdots　② \\ 　s-t &=& z+1　　\cdots\cdots　③ \\ \end{array} \right. \]

　①，②より

$s=1$，$t=-1$

　③に代入すると

$z=1$

● 点と平面

　$3$ 点を通る平面は１つだけ

● 同一平面上にある点

　平面 $ABC$ 上に点 $P$ があるとき

$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$

　を満たす実数 $s$，$t$ が存在する

空間ベクトルの応用問題によく使われるのでマスターしておこう！