和の記号Σ

数列の記号のΣについて学ぼう!
数列 $\{a_n\}$ について,初項から第 $n$ 項までの和を,第 $k$ 項 $a_k$ と和の記号Σを用いて
$\displaystyle{\sum_{k=1}^{n}a_k}$
と表す
$\displaystyle{\sum_{k=1}^{n}a_k=a_1+a_2+a_3+\cdots\cdots+a_n}$
一般に
$\displaystyle{\sum_{k=○}^{□}a_k}$
は,数列 $\{a_k\}$ の第○項から第□項までの和を表す
つまり,$k=○$ から $k=□$ までを順に $a_k$ に代入して足し合わせたものを表す
$k$ の代わりに
$\displaystyle{\sum_{i=○}^{□}a_i}$
や
$\displaystyle{\sum_{j=○}^{□}a_j}$
のように別の文字を用いてもよい
次の式を和の形でかけ。
(1) $\displaystyle{\sum_{k=1}^{n}k}$
(2) $\displaystyle{\sum_{k=2}^{20}(2k-1)}$
(3) $\displaystyle{\sum_{k=1}^{n-1}2^k}$
(1) $\displaystyle{\sum_{k=1}^{n}k}$
$k=1$ から $k=n$ までを順に $k$ に代入して足し合わせたもの
$\displaystyle{\sum_{k=1}^{n}k=1+2+3+\cdots\cdots+n}$
(2) $\displaystyle{\sum_{k=2}^{8}(2k-1)}$
$k=2$ から $k=20$ までを順に $2k-1$ に代入して足し合わせたもの
$\displaystyle{\sum_{k=2}^{20}(2k-1)=3+5+7+\cdots\cdots+39}$
(3) $\displaystyle{\sum_{k=1}^{n-1}2^k}$
$k=1$ から $k=n-1$ までを順に $2^k$ に代入して足し合わせたもの
$\displaystyle{\sum_{k=1}^{n-1}2^k=2^1+2^2+2^3+\cdots\cdots+2^{n-1}}$

考えているΣが,どういう数列の和なのかを知っておくことが大切!
和をΣで表す

次は和をΣで表してみよう!
$\displaystyle{\sum_{k=2}^{14}k}$
$\displaystyle{\sum_{i=2}^{14}i}$
$\displaystyle{\sum_{k=1}^{13}(k+1)}$

和をΣで表す方法はたくさんあるね!
自然数に関する和の公式

重要なΣの公式をおさえよう!
$\displaystyle{\sum_{k=1}^{n}c=nc}$
$\displaystyle{\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)}$
$\displaystyle{\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)}$
● $\displaystyle{\sum_{k=1}^{n}c=nc}$
$\displaystyle{\sum_{k=1}^{n}c}$ は $c$ という定数の数列を初項から第 $n$ 項までの $n$ 個を足し合わせたもの
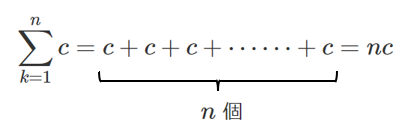
● $\displaystyle{\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)}$
$\displaystyle{\sum_{k=1}^{n}k}$ は $k=1$ から $k=n$ を順に $k$ に代入して足し合わせたものなので
$\displaystyle{\sum_{k=1}^{n}k=1+2+3+\cdots\cdots+n}$
ここで, $1+2+3+\cdots\cdots+n$ を考えると
初項 $1$,末項 $n$,項数 $n$ の等差数列の和
等差数列の和の公式より,初項 $a$,末項 $l$,項数 $n$ の等差数列の和は
$\displaystyle{\frac{1}{2}n(a+l)}$ なので
$\displaystyle{1+2+3+\cdots\cdots+n=\frac{1}{2}n(n+1)}$
したがって,
$\displaystyle{\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)}$
● $\displaystyle{\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)}$
$\displaystyle{\sum_{k=1}^{n}k^2}$ は $k=1$ から $k=n$ を順に $k^2$ に代入して足し合わせたものなので
$\displaystyle{\sum_{k=1}^{n}k^2=1^2+2^2+3^2+\cdots\cdots+n^2}$
つまり, $\displaystyle{\sum_{k=1}^{n}k^2}$ は自然数の $2$ 乗の和
恒等式 $k^3-(k-1)^3=3k^2-3k+1$ を利用する
$k$ に $1$ から $n$ までを順に代入すると
\begin{eqnarray} k&=&1 1^3-0^3 &=& 3\cdot 1^3-3\cdot1+1 \\\\ k&=&2 2^3-1^3 &=& 3\cdot 2^3-3\cdot2+1 \\\\ k&=&3 3^3-2^3 &=& 3\cdot 3^3-3\cdot3+1 \\\\ &\cdots& \cdots\cdots \\\\ k&=&n n^3-(n-1)^3 &=& 3\cdot n^3-3\cdot n+1 \end{eqnarray}これら $n$ 個の等式の辺々を加えると
$n^3=3(1^2+2^2+3^2+\cdots\cdots+n^2)-3(1+2+3+\cdots\cdots+n)+n$
すなわち
$\displaystyle{n^3=3S-3\cdot\frac{1}{2}n(n+1)+n}$
$6S=2n^3+3n(n+1)-2n$
$6S=n(n+1)(2n+1)$
$\displaystyle{S=\frac{1}{6}n(n+1)(2n+1)}$
したがって
$\displaystyle{1^2+2^2+3^2+\cdots\cdots+n^2=\frac{1}{6}n(n+1)(2n+1)}$
以上より
$\displaystyle{\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)}$
問題
次の和を求めよ。
(1) $\displaystyle{\sum_{k=1}^{10}2}$
(2) $\displaystyle{\sum_{k=1}^{10}k}$
(3) $\displaystyle{\sum_{k=1}^{10}k^2}$
(1) $\displaystyle{\sum_{k=1}^{10}2}$
$\displaystyle{\sum_{k=1}^{10}2=10\cdot2=20}$
(2) $\displaystyle{\sum_{k=1}^{10}k}$
$\displaystyle{\sum_{k=1}^{10}k=\frac{1}{2}\cdot10\cdot11=55}$
(3) $\displaystyle{\sum_{k=1}^{10}k^2}$
$\displaystyle{\sum_{k=1}^{10}k^2=\frac{1}{6}\cdot10\cdot11\cdot21=385}$

Σが数列の和であることを理解して計算できるようにしよう!




コメント