絶対値の方程式と不等式の問題の中でも難易度が高い『場合分けが必要な絶対値の方程式と不等式』の解き方をわかりやすく解説します!
場合分けのやり方をおさえれば,誰でも必ず解けるようになります!
解けるようになって,周りの人と差をつけよう!

今回解説する問題はこれ!
(1) $|x+1|=2x$
(2) $|2x-6| < x+3$
(3) $|x+1|+|x-2|=x+3$
絶対値記号のはずし方の基本

絶対値ってそもそも何だっけ?

絶対値は「原点からの距離を表す記号」だよ!
絶対値の基本を学ぶならこれ!

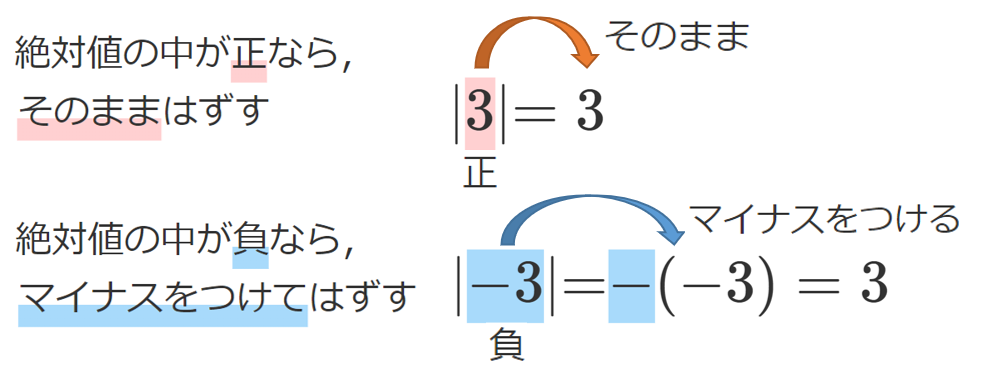

絶対値の中の符号が分かれば,絶対値をはずすことができるよ!
場合分けによる絶対値記号のはずし方

場合分けによる絶対値記号のはずし方を学ぼう!
これを使って,絶対値の方程式と不等式を解くよ!

$$|x-1|$$
絶対値の中 $x-1$ が正($0$ 以上)のとき
$x-1≧0$ すなわち $x≧1$ のとき
$|x-1|=x-1$
(そのままはずす)
絶対値の中 $x-1$ が負のとき
$x-1<0$ すなわち $x < 1$ のとき
$|x-1|=-(x-1)=-x+1$
(マイナスをつけてはずす)
まとめると
\begin{align} &|x-1|=\left\{ \begin{array}{ll} x-1 (x≧1 のとき) \\ -x+1 (x<1 のとき) \end{array} \right. \end{align}場合分けが必要な絶対値の方程式

$|x|=2$ は $x=\pm2$ と簡単に解けるけど,
下の問題のように,絶対値の外にも $x$ が入っている方程式や不等式は場合分けが必要だよ!
絶対値の中 $x+1$ が正($0$ 以上)のとき
$x+1≧0$ すなわち $x≧-1$ のとき
$|x+1|=x+1$
(そのままはずす)
絶対値の中 $x+1$ が負のとき
$x+1<0$ すなわち $x < -1$ のとき
$|x+1|=-(x+1)=-x-1$ (マイナスをつけてはずす)
まとめると
\begin{align} &|x+1|=\left\{ \begin{array}{ll} x+1 (x≧-1 のとき) \\ -x-1 (x<-1 のとき) \end{array} \right. \end{align} [1] $x+1≧0$ すなわち $x ≧ -1$ のとき
(絶対値の中が $0$ 以上のとき)
これは $x ≧ -1$ を満たす
場合分けの条件を満たしているか確認する
[2] $x+1 < 0$ すなわち $x < -1$ のとき
(絶対値の中が負のとき)
これは $x < -1$ を満たさないため不適
場合分けの条件を満たしているか確認する
[1],[2] より
$x=1$(答)

出てきた解が場合分けの条件を満たすかどうか確認することが重要だね!
場合分けが必要な絶対値の不等式
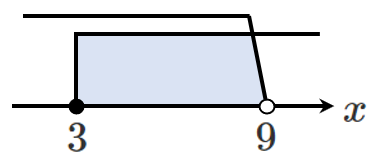
[1] $2x-6≧0$ すなわち $x ≧ 3$ のとき
(絶対値の中が $0$ 以上のとき)
$x ≧ 3$ と共通範囲をとって $3 ≦ x < 9$
場合分けの条件と共通範囲をとる
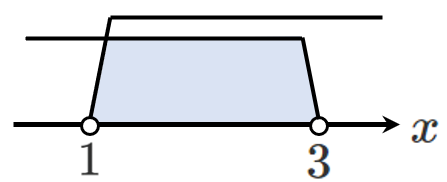
[2] $2x-6 < 0$ すなわち $x < 3$ のとき
(絶対値の中が負のとき)
$x < 3$ と共通範囲をとって $1 < x < 3$
場合分けの条件と共通範囲をとる
[1],[2] より, $1 < x < 3$ または $3 ≦ x < 9$
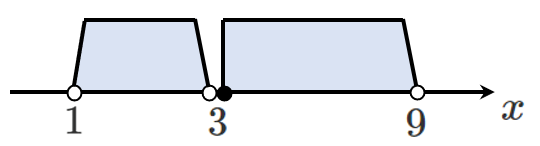
$1 < x < 9$(答)

出てきた解と場合分けの条件の共通範囲をとることが重要だね!
場合分けによる絶対値記号のはずし方【2つ】

絶対値が2つのときの,場合分けの考え方も学ぼう!
詳しく学びたい人はこれ↓
$$|x+1|+|x-2|$$
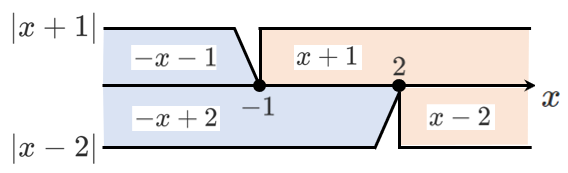
$x < -1$ のとき
$|x+1|=-x-1$,$|x-2|=-x+2$ なので
$-1 ≦ x < 2$ のとき
$|x+1|=x+1$,$|x-2|=-x+2$ なので
$2 ≦ x$ のとき
$|x+1|=x+1$,$|x-2|=x-2$ なので
まとめると
\begin{align} &|x+1|+|x-2|=\left\{ \begin{array}{lll} -2x+1 (x<-1 のとき) \\ 3 (-1 ≦ x < 2 のとき) \\ 2x-1 (2≦x のとき) \end{array} \right. \end{align}場合分けが必要な絶対値の方程式【2つ】

1つ前の問題を参考に場合分けをして,絶対値が2つある方程式を解いてみよう!
[1] $x < -1$ のとき
\begin{eqnarray} |x+1|+|x-2| & = & x+3 \\ -(x+1)-(x-2) & = & x+3 \\ x & = & -\frac{2}{3} \end{eqnarray}これは $x < -1$ を満たさないため不適
場合分けの条件を満たしているか確認する
[2] $-1 ≦ x < 2$ のとき
\begin{eqnarray} |x+1|+|x-2| & = & x+3 \\ (x+1)-(x-2) & = & x+3 \\ x & = & 0 \end{eqnarray}これは $-1 ≦ x < 2$ を満たす
場合分けの条件を満たしているか確認する
[3] $2 ≦ x$ のとき
\begin{eqnarray} |x+1|+|x-2| & = & x+3 \\ (x+1)+(x-2) & = & x+3 \\ x & = & 4 \end{eqnarray}これは $2 ≦ x$ を満たす
場合分けの条件を満たしているか確認する
[1],[2],[3] より,
$x=0$,$4$(答)

これが解けるようになったら,
場合分けが必要な絶対値の方程式と不等式は完璧!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント