
苦手な人が多い!
微分係数の定義式について理解しよう!
微分係数の定義式
関数 $f(x)$ の $x=a$ の微分係数
$f'(a)=\displaystyle \lim_{h \to 0} \frac{f(a+h)-f(a)}{(a+h)-a}$

微分の基本中の基本が「微分係数の定義式」!
微分について理解するためには必要不可欠!

「微分係数の定義式」は式が複雑だから,結局何を表している式かよくわからないよー!

1つ1つ意味を理解していけば,必ず分かる!
一緒に学んでみよう!
平均変化率

「微分係数の定義式」を学ぶ前に「平均変化率」と「極限値」について学ぼう!
関数 $y=f(x)$ において,$x$ の値が $a$ から $b$ まで変化するとき
$\displaystyle{\frac{y の変化量}{x の変化量}=\frac{f(b)-f(a)}{b-a}}$
を,$x=a$ から $x=b$ までの関数 $y=f(x)$ の平均変化率という
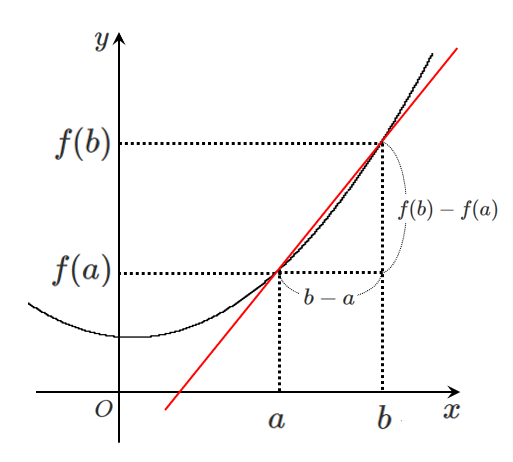
平均変化率は,関数 $y=f(x)$ のグラフ上の $2$ 点 $A(a,f(a))$,$B(b,f(b))$ を通る直線 $AB$ の傾きを表す

中学でも習った
$\displaystyle{\frac{y の変化量}{x の変化量}}$
を平均変化率というよ!
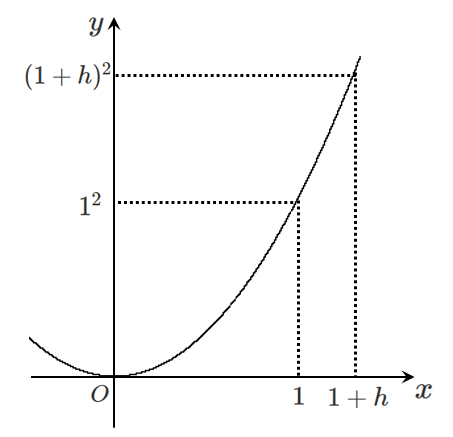
$\displaystyle{\frac{(1+h)^2-1^2}{(1+h)-1}=\frac{2h+h^2}{h}=\frac{h(2+h)}{h}=2+h}$
極限値
ある文字をある値に限りなく近づけるとき
$\lim$ の記号を用いる
例えば
$2+h$ において,$h$ が $0$ に限りなく近づける
を式で表すと
$\displaystyle{\lim_{h \to 0} (2+h)}$
$h$ が限りなく $0$ に近づくとき,$2+h$ は $2$ に限りなく近づくので
$\displaystyle{\lim_{h \to 0} (2+h)=2}$
次の極限値を求めよ。
(1) $\displaystyle{\lim_{h \to 0} (1-h)}$
(2) $\displaystyle{\lim_{h \to 0} (3-2h+h^2)}$
(1) $\displaystyle{\lim_{h \to 0} (1-h)}$
$\displaystyle{\lim_{h \to 0} (1-h)=1}$
(2) $\displaystyle{\lim_{h \to 0} (3-2h+h^2)}$
$\displaystyle{\lim_{h \to 0} (3-2h+h^2)=3}$

$h$ を限りなく $0$ に近づけることは,$h=0$ を代入することと同じ意味ではないので要注意!
曲線の接線の傾き

微分係数を理解するには,曲線における接線の傾きの考え方を理解する必要があるよ!
①曲線上に $2$ 点 $A$,$P$ をとる
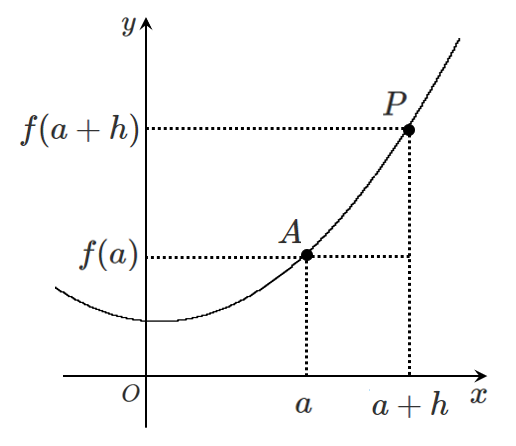
関数 $y=f(x)$ のグラフ上に $2$ 点 $A(a,f(a))$,$P(a+h,f(a+h))$ をとる
② $2$ 点を結ぶ直線 $AP$ の傾き(平均変化率)を考える
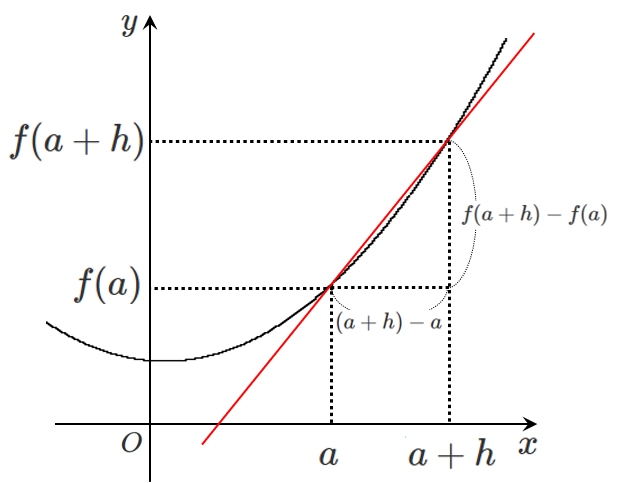
直線 $AP$ の傾き(平均変化率)は
$\displaystyle{\frac{f(a+h)-f(a)}{(a+h)-a}}$
③点 $P$ を点 $A$ に限りなく近づける
点 $P$ を点 $A$ に限りなく近づけるとき,
$h \to 0$
を考えればよい
④直線 $AP$ の傾きが点 $A$ における接線の傾きに近づく
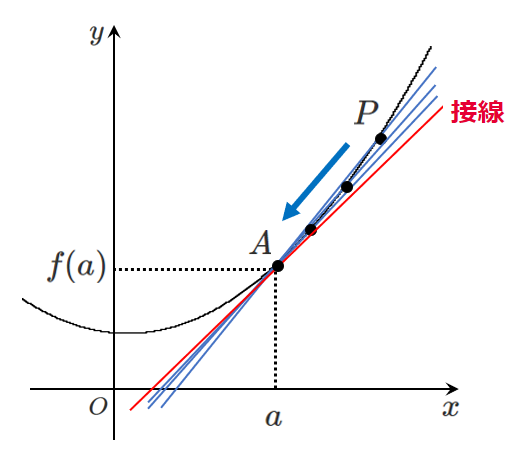
直線 $AP$ の傾き
$\displaystyle{\frac{f(a+h)-f(a)}{(a+h)-a}}$
について,$h \to 0$ を考えると
$\displaystyle{\lim_{h \to 0}\frac{f(a+h)-f(a)}{(a+h)-a}}$
は点 $A$ すなわち $x=a$ における接線の傾きである
関数 $f(x)$ の $x=a$ における接線の傾きは
$\displaystyle{f'(a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{(a+h)-a}}$
微分係数は接線の傾き
関数 $f(x)$ の $x=a$ の微分係数
$\displaystyle{f'(a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{(a+h)-a}}$

「微分係数の定義式」と「接線の傾き」は同じ式で表されている!
つまり,微分係数と接線の傾きは等しい!
関数 $y=f(x)$ の $x=a$ における微分係数 $f'(a)$ は
関数 $y=f(x)$ のグラフ上の点 $A(a,f(a))$ における接線の傾きと等しい

「微分係数」という名前でみると難しそうだけど,「接線の傾き」と考えれば何のことか分かりやすいね!
問題
次の値を求めよ
(1) 関数 $f(x)=3x^2$ の $x=1$ における微分係数
(2) 関数 $f(x)=x^2$ 上の点 $(-1,1)$ における接線の傾き
(1) 関数 $f(x)=3x^2$ の $x=1$ における微分係数
$\displaystyle{f'(1)=\lim_{h \to 0} \frac{f(1+h)-f(1)}{(1+h)-1}= \lim_{h \to 0} \frac{(1+h)^2-1^2}{h} }$
$\displaystyle{=\lim_{h \to 0} \frac{2h+h^2}{h}= \lim_{h \to 0} \frac{h(2+h)}{h} }$
$\displaystyle{=\lim_{h \to 0} (2+h)=2}$
(2) 関数 $f(x)=x^2$ 上の点 $(-1,1)$ における接線の傾き
$\displaystyle{f'(-1)=\lim_{h \to 0} \frac{f(-1+h)-f(-1)}{(1+h)-1}= \lim_{h \to 0} \frac{(-1+h)^2-(-1)^2}{h} }$
$\displaystyle{=\lim_{h \to 0} \frac{-2h+h^2}{h}= \lim_{h \to 0} \frac{h(-2+h)}{h} }$
$\displaystyle{=\lim_{h \to 0} (-2+h)=-2}$
まとめ
● 微分係数の定義式
関数 $f(x)$ の $x=a$ の微分係数
$f'(a)=\displaystyle \lim_{h \to 0} \frac{f(a+h)-f(a)}{(a+h)-a}$
● 微分係数と接線の傾きの関係
関数 $y=f(x)$ の $x=a$ における微分係数 $f'(a)$ は
関数 $y=f(x)$ のグラフ上の点 $A(a,f(a))$ における接線の傾きと等しい

微分係数と接線の傾きは等しいということをおさえよう!




コメント