この投稿は,高校数学Ⅰ『2次関数』の大学入試合格に向けたロードマップをまとめたものです。
基本問題から応用問題まで幅広く,単元の中で取り組むべき内容をまとめました。
2次関数の基本
平方完成
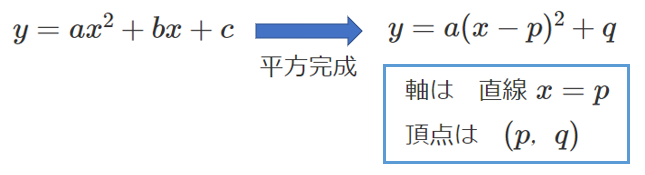
平方完成とは、$y=ax^2+bx+c$ を $y=a(x-p)^2+q$ という形に変形することです。
$y=a(x-p)^2+q$ の形に変形することで、軸と頂点を求めることができます。
(1) $y=x^2-2x-1$
(2) $y=x^2+x+1$
(3) $y=2x^2+4x+1$
(4) $y=-x^2+2x-3$
(5) $y=2x^2+3x+2$
(6) $y=-2x^2+2x+3$
(7) $y=\frac{1}{2}x^2+x-1$
(8) $y=x^2-2ax+a$
(9) $y=ax^2+2ax-2$
(10) $y=x^2-2(a-1)x+1$
\begin{eqnarray} (1) y &=& x^2-2x-1 \\ &=& (x-1)^2-1^2-1\\ &=& (x-1)^2-2 \\\\ &&頂点は (1,-2) \\\\ (2) y &=& x^2+x+1 \\ &=& \left(x+\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+1\\ &=& \left(x+\frac{1}{2}\right)^2+\frac{3}{4} \\\\ &&頂点は \left(-\frac{1}{2},\frac{3}{4}\right) \\\\ (3) y &=& 2x^2+4x+1 \\ &=& 2(x^2+2x)+1\\ &=& 2\{(x+1)^2-1^2\}-1\\ &=& 2(x+1)^2-2-1\\ &=& 2(x+1)^2-3 \\\\ &&頂点は \left(-1,-3\right) \\\\ (4) y &=& -x^2+2x-3 \\ &=& -(x^2-2x)-3\\ &=& -\{(x-1)^2-1^2\}-3\\ &=& -(x-1)^2+1-3\\ &=& -(x-1)^2-2 \\\\ &&頂点は (1,-2) \\\\ (5) y &=& 2x^2+3x+2 \\ &=& 2\left(x^2+\frac{3}{2}x\right)+2\\ &=& 2\left\{\left(x+\frac{3}{4}\right)^2-\left(\frac{3}{4}\right)^2\right\}+2\\ &=& 2\left(x+\frac{3}{4}\right)^2-\frac{9}{8}+2\\ &=& 2\left(x+\frac{3}{4}\right)^2+\frac{7}{8} \\\\ &&頂点は \left(-\frac{3}{4},\frac{7}{8}\right) \\\\ (6) y &=& -2x^2+2x+3 \\ &=& -2\left(x^2-x\right)+3\\ &=& -2\left\{\left(x-\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\right\}+3\\ &=& -2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}+3\\ &=& -2\left(x-\frac{1}{2}\right)^2+\frac{7}{2} \\\\ &&頂点は \left(\frac{1}{2},\frac{7}{2}\right) \\\\ (7) y &=& \frac{1}{2}x^2+x-1 \\ &=& \frac{1}{2}\left(x^2+2x\right)-1\\ &=& \frac{1}{2}\left\{\left(x+1\right)^2-1^2\right\}-1\\ &=& \frac{1}{2}\left(x+1\right)^2-\frac{1}{2}-1\\ &=& \frac{1}{2}\left(x+1\right)^2-\frac{3}{2} \\\\ &&頂点は \left(-1,-\frac{3}{2}\right) \\\\ (8) y &=& x^2-2ax+a \\ &=& \left(x-a\right)^2-a^2+a\\ &=& \left(x-a\right)^2-a^2+a \\\\ &&頂点は \left(a,-a^2+a\right) \\\\ (9) y &=& ax^2+2ax-2 \\ &=& a(x^2+2x)-2\\ &=& a\{(x+1)^2-1^2\}-2\\ &=& a(x+1)^2-a-2\\\\ &&頂点は \left(-1,-a-2\right) \\\\ (10) y &=& x^2-2(a-1)x+1 \\ &=& \{x-(a-1)\}^2-(a-1)^2+1\\ &=& \{x-(a-1)\}^2-a^2+2a \\\\ &&頂点は (a-1,-a^2+2a) \\\\ \end{eqnarray}
平方完成を学ぶ↓



平行移動・対称移動
2.頂点の移動を考える
3.$x^2$ の係数($a$ の値)は変わらない
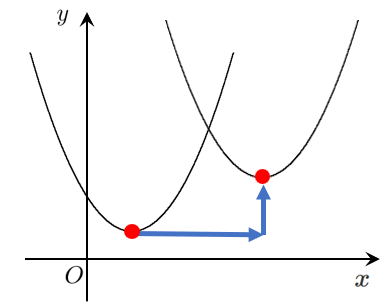
(1) ①のグラフを $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して得られるグラフ
(2) $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して①のグラフと重なるようなグラフ
を求めよ。
①について $y=2(x-1)^2+2$
よって,①のグラフの頂点は $(1,2)$
(1)
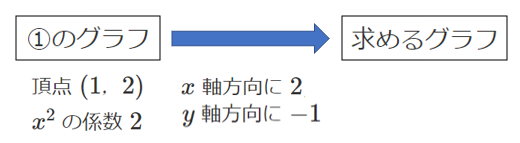
①のグラフの頂点 $(1,2)$ を
$x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動すると $(3,1)$
求めるグラフは,①のグラフを平行移動したものであるから
$x^2$ の係数は $2$ である
よって,求める方程式は $y=2(x-3)^2+1$
(2)

①のグラフの頂点 $(1,2)$ を
$x$ 軸方向に $-2$,$y$ 軸方向に $1$ だけ平行移動したものであるから
頂点は $(-1,3)$,$x^2$ の係数は $2$ である
よって,求める方程式は $y=2(x+1)^2+3$
(1) ①のグラフを $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して得られるグラフ
(2) $x$ 軸方向に $2$,$y$ 軸方向に $-1$ だけ平行移動して①のグラフと重なるようなグラフ
を求めよ。
(1) $y-(-1)=2(x-2)^2-4(x-2)+4$ ← $x$ を $x-2$,$y$ を $y-(-1)$
これを計算して $y=2x^2-8x+19$
(2) 求めるグラフは①のグラフを
$x$ 軸方向に $-2$,$y$ 軸方向に $1$ だけ平行移動したものであるから
$y-1=2(x+2)^2-4(x+2)+4$ ← $x$ を $x+2$,$y$ を $y-1$
これを計算して $y=2x^2+4x+5$
2.$x^2$ の係数($a$ の値)について
$y$ 軸に関する対称移動は符号が変わらない
$x$ 軸,原点に関する対称移動は符号が変わる
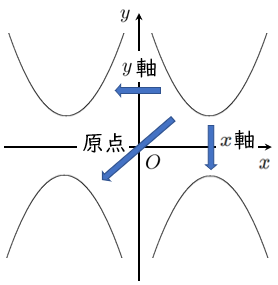
(1) $x$ 軸に関する対称移動したグラフ
(2) $y$ 軸に関して対称移動したグラフ
(3) 原点に関して対称移動したグラフ
を求めよ。
①について $y=2(x-1)^2+2$
よって,①のグラフの頂点は $(1,2)$
(1) ①のグラフの頂点を $x$ 軸に関して対称移動すると $(1,-2)$
グラフの形は下に凸から上に凸に変わるので $y=-2(x-1)^2-2$
(2) ①のグラフの頂点を $x$ 軸に関して対称移動すると $(-1,2)$
グラフの形は変わらないので $y=2(x+1)^2+2$
(3) ①のグラフの頂点を原点に関して対称移動すると $(-1,-2)$
グラフの形は下に凸から上に凸に変わるので $y=-2(x+1)^2-2$
$y$ 軸に関して対称移動したいときは $x$ を $-x$ にする
原点に関して対称移動したいときは $x$ を $-x$,$y$ を $-y$ にする
(1) $x$ 軸に関する対称移動したグラフ
(2) $y$ 軸に関して対称移動したグラフ
(3) 原点に関して対称移動したグラフ
を求めよ。
(1) $-y=2x^2-4x+4$ ← $y$ を $-y$ にする
これを計算すると $y=-2x^2+4x-4$
(2) $y=2(-x)^2-4\cdot(-x)+4$ ← $x$ を $-x$ にする
これを計算すると $y=2x^2+4x+4$
(2) $-y=2(-x)^2-4\cdot(-x)+4$ ← $x$ を $-x$,$y$ を $-y$ にする
これを計算すると $y=-2x^2-4x-4$
平行移動・対称移動を学ぶ↓

2次関数の最大・最小
定義域における最大・最小
関数 $y=f(x)$ において
定義域 … 変数 $x$ のとりうる値の範囲
値域 … $x$ が定義域内のすべての値をとるときの $y$ のとりうる値の範囲
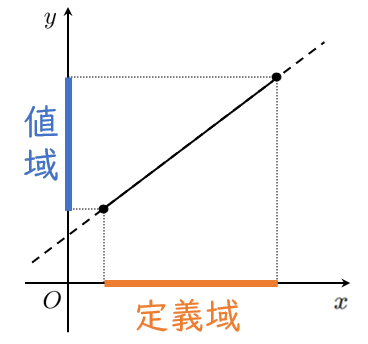
グラフを図示するとき,定義域内は実線,定義域外は点線で表すことが多い
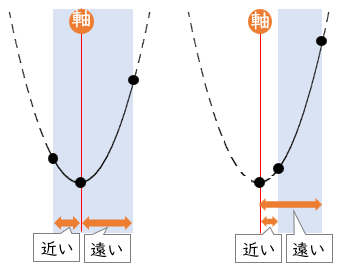
・最大値・最小値は,『頂点』か『定義域の端点』のいずれかでとる
・放物線は軸に関して対称
・軸と定義域の端点の距離を注意してグラフをかく
(1) $y=x^2-4x+1$ ($0≦x≦3$)
(2) $y=-x^2-2x+3$ ($0≦x≦2$)
(1) $y=(x-2)^2-3$ 軸は $x=2$,頂点は $(2,-3)$
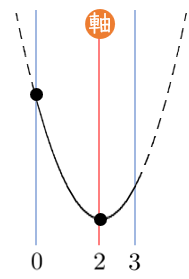
$x=0$ で最大値 $1$,$x=2$ で最小値 $-3$
(2) $y=-(x+1)^2+4$ 軸は $x=-1$,頂点は $(-1,4)$
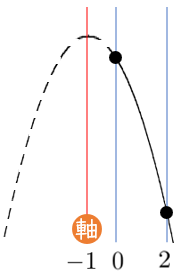
$x=0$ で最大値 $3$,$x=2$ で最小値
2次関数の最大・最小を学ぶ↓

最大・最小からの係数の決定
平方完成すると $y=(x-1)^2-1+c$ となり、軸は直線 $x=1$
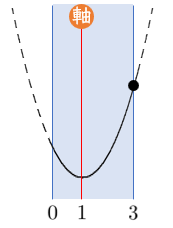
$x=3$ で最大値をとる
このとき、$x=3$ を代入すると $y=(3-1)^2-1+c=3+c$
これが $7$ になるので $3+c=7$ より $c=4$

軸と定義域の位置関係から、『$x=□$ で最大値をとるか』を考えることがポイント!
軸に定数を含む
『軸』や『定義域』の位置によって最大・最小が変わるので、場合分けを考える

まずは、軸に定数を含む問題だね!
場合分けを考えてみよう!
$f(x)=(x-a)^2-a^2+2$
軸は 直線 $x=a$,頂点は $(a,-a^2+2)$
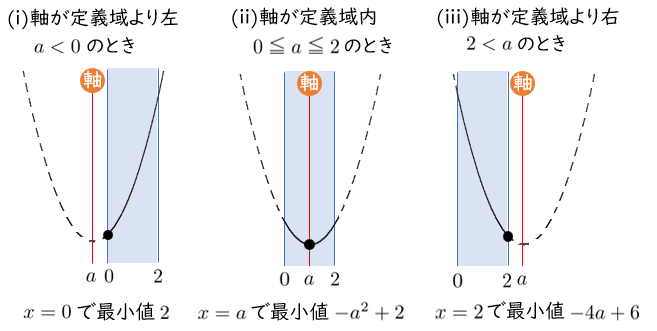
$a<0$ のとき $x=0$ で最小値 $2$
$0≦a≦2$ のとき $x=a$ で最小値 $-a^2+2$
$2<a$ のとき $x=2$ で最小値 $-4a+6$
$f(x)=(x-a)^2-a^2+2$
軸は 直線 $x=a$,頂点は $(a,-a^2+2)$
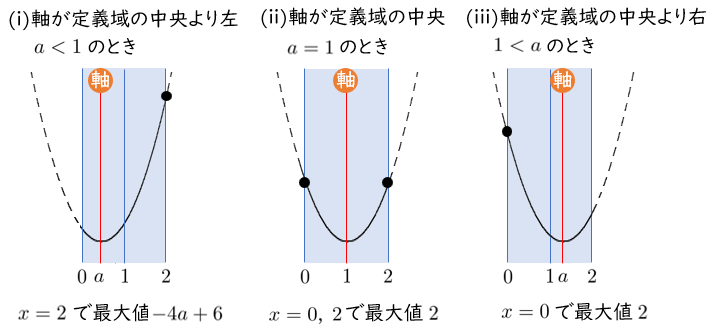
$a<1$ のとき $x=2$ で最大値 $-4a+6$
$a=1$ のとき $x=0,2$ で最大値 $2$
$1<a$ のとき $x=0$ で最大値 $2$
●下に凸の場合
最小値は、軸が定義域の左・内・右で場合分け
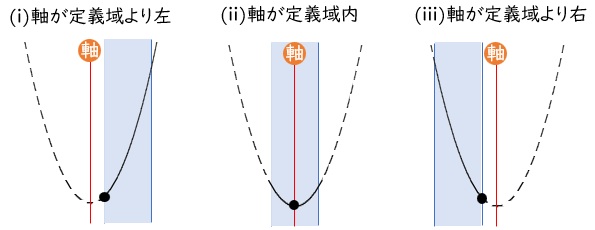
最大値は、軸が定義域の中央より左・中央・中央より右で場合分け
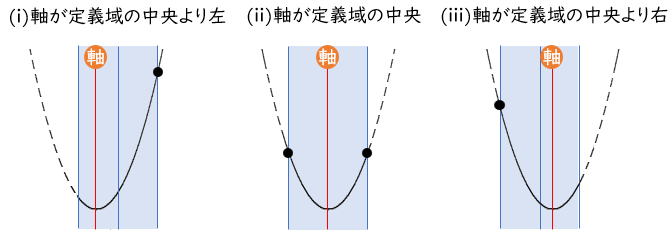
●上に凸の場合
最小値は、軸が定義域の中央より左・中央・中央より右で場合分け
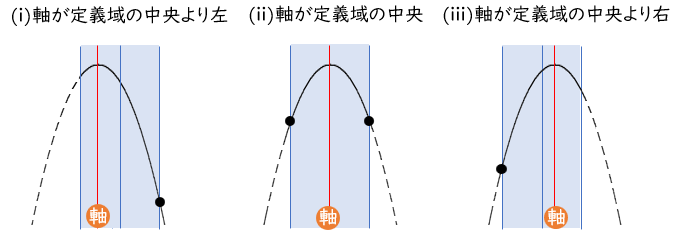
最大値は、軸が定義域の左・内・右で場合分け

下に凸の最小値と上に凸の最大値
下に凸の最大値と上に凸の最小値
の場合分けの考え方は同じだね!
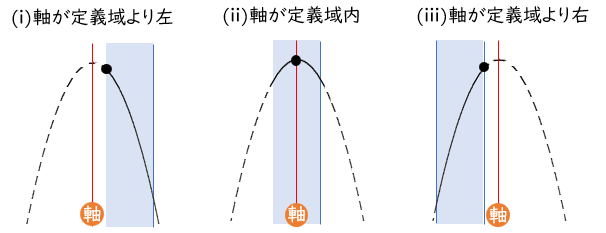
定義域の片端に定数を含む

次は、定義域の右端に定数が含まれる問題だよ!
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$
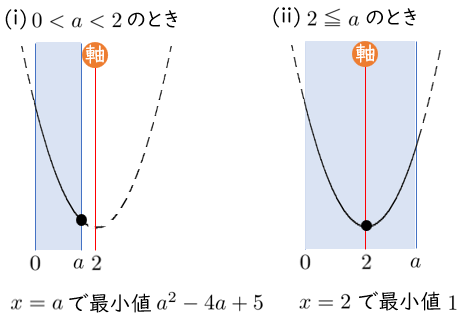
$0<a<2$ のとき $x=a$ で最小値 $a^2-4a+5$
$2≦a$ のとき $x=2$ で最小値 $1$
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$
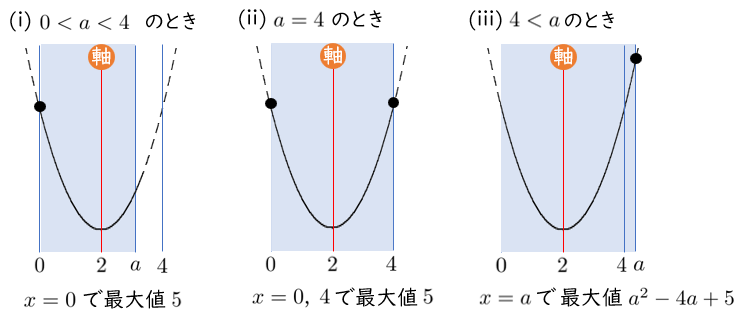
$0<a<4$ のとき $x=0$ で最大値 $5$
$a=4$ のとき $x=0,4$ で最大値 $5$
$4<a$ のとき $x=a$ で最大値 $a^2-4a+5$
定義域の両端に定数を含む
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$
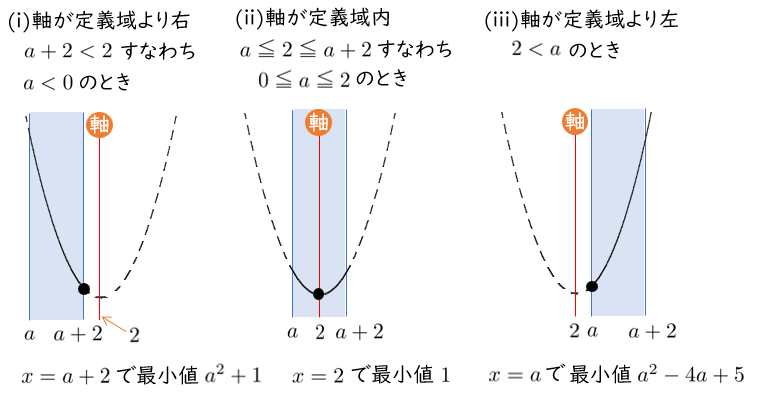
$a<0$ のとき $x=a+2$ で最小値 $a^2+1$
$0≦a≦2$ のとき $x=2$ で最小値 $1$
$2<a$ のとき $x=a$ で最小値 $a^2-4a+5$
$f(x)=(x-2)^2+1$
軸は 直線 $x=2$,頂点 $(2,1)$
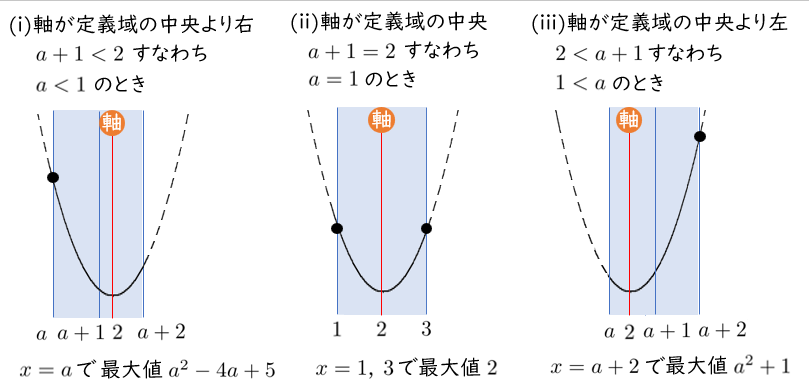
$a<1$ のとき $x=a$ で最大値 $a^2-4a+5$
$a=1$ のとき $x=1,3$ で最大値 $2$
$1<a$ のとき $a=a+2$ で最大値 $a^2+1$
最小値は、軸が定義域の右・内・左で場合分け
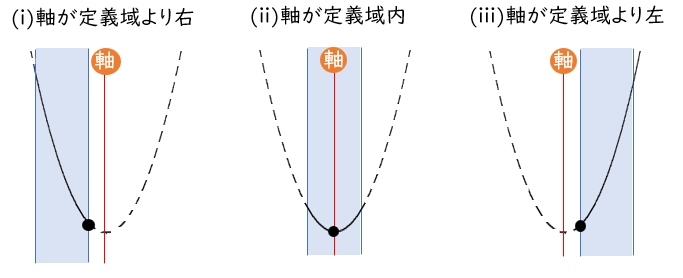
最大値は、軸が定義域の中央より右・中央・中央より左で場合分け
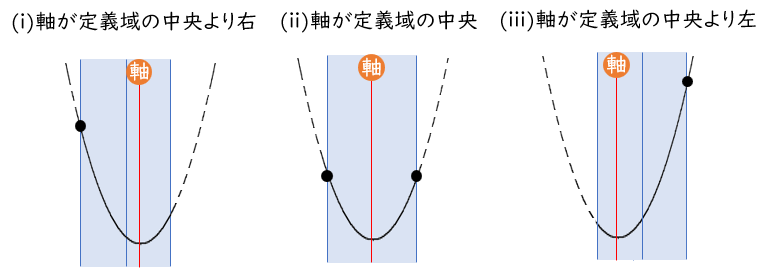
●上に凸の場合
最小値は、軸が定義域の中央より左・中央・中央より右で場合分け
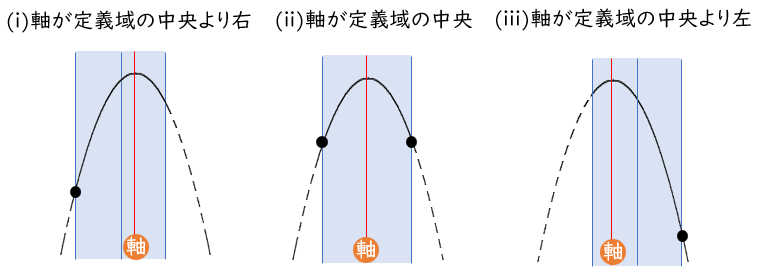
最大値は、軸が定義域の左・内・右で場合分け
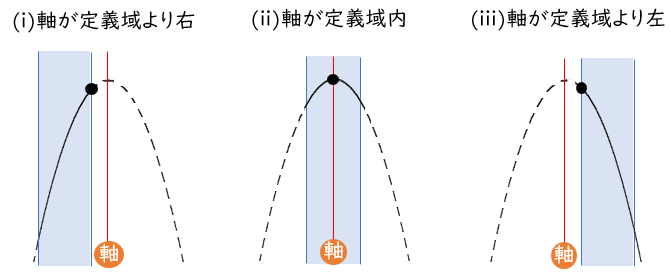
2次関数の決定
② $y=a(x-p)^2+q$ 【基本形】 軸・頂点がわかる式
③ $y=a(x-\alpha)(x-\beta)$ 【因数分解形】 $x$ 軸との共有点がわかる式

与えられた条件から①~③の式を選んで式で表す!
基本形と一般形の応用
(1) 頂点が $(2,1)$ で点 $(4,5)$ を通る2次関数
(2) 軸が直線 $x=1$ で,2点 $(0,1)$,$(3,-2)$ を通る2次関数
(1) 頂点が $(2,1)$ より $y=a(x-2)^2+1$ ($a≠0$) とおくと
$(4,5)$ を通るので $5=a(4-2)^2+1$ ←「通る」は代入
これを解いて $a=1$
したがって,求める2次関数は $y=(x-2)^2+1$
(2) 軸が 直線 $x=1$ より $y=a(x-1)^2+q$ ($a≠0$) とおくと
$(0,1)$ を通るので $1=a(0-1)^2+q$
$a+q=1$ … ①
$(3,-2)$ を通るので $-2=a(3-1)^2+q$
$4a+q=-2$ … ②
①,②を解いて $a=-1$,$q=2$
求める2次関数は $y=-(x-1)^2+2$
$y=ax^2+bx+c$ ($a≠0$) とおくと
$(1,1)$ を通るので $a+b+c=1$ … ①
$(2,6)$ を通るので $4a+2b+c=6$ … ②
$(3,13)$ を通るので $9a+3b+c=13$ … ③
①,②,③を解いて $a=1$,$b=2$,$c=-2$
求める2次関数は $y=x^2+2x-2$
基本形・一般形の利用を学ぶ↓

因数分解形の利用
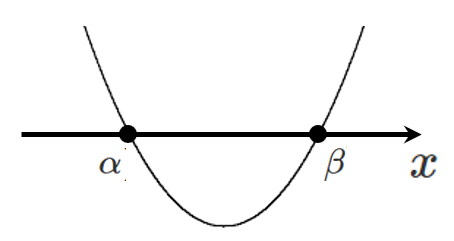
問題
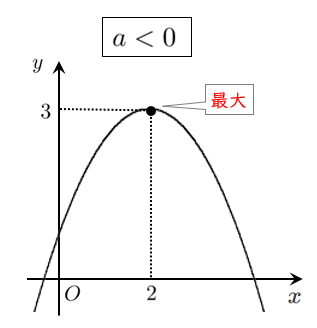
$x$ 軸と $(-1,0)$,$(5,0)$ で交わるので
$y=a(x+1)(x-5)$ ($a≠0$) とおくと
$(0,5)$ を通るので $5=a(0+1)(0-5)$
これを解いて $a=-1$
求める2次関数は $y=-(x+1)(x-5)$
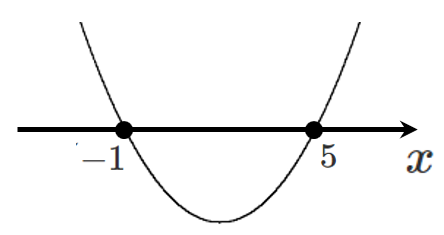
最大・最小からの決定
頂点に関する条件により、基本形 $y=a(x-p)^2+q$ を利用して解く
$x=2$ のとき最大値 $3$ をとるので,求める2次関数は
頂点が $(2,3)$ で上に凸の放物線である
よって $y=a(x-2)^2+3$ ($a<0$) とおくと
$(1,2)$ を通るので $2=a(1-2)^2+3$
これを解いて $a=-1$ ($a<0$ を満たす)
求める2次関数は $y=-(x-2)^2+3$
2次方程式
2次方程式 $ax^2+bx+c=0$ の解き方
①左辺を因数分解して解く
2次方程式 $a(x-\alpha)(x-\beta)=0$ を解くと $x=\alpha,\beta$
②解の公式を用いて解く
2次方程式 $ax^2+bx+c=0$ を解くと $\displaystyle{x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}}$
2次方程式の解の公式
2次方程式 $ax^2+bx+c=0$ の解は $\displaystyle{x=\frac{-b±\sqrt{b^2-4ac}}{2a}}$
特に,$b$ が偶数のとき $\displaystyle{x=\frac{-(bの半分)\pm\sqrt{(bの半分)^2-ac}}{a}}$
$$ax^2+bx+c=0$$
$$a\left(x^2+\frac{b}{a}x\right)+c=0$$
$$a\left\{\left(x+\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2\right\}+c=0$$
$$a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}+c=0$$
$$a\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a}$$
$$\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$$
$$x+\frac{b}{2a}=±\frac{\sqrt{b^2-4ac}}{2a}$$
$$x=-\frac{b}{2a}±\frac{\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-b±\sqrt{b^2-4ac}}{2a}$$
(1) $3x^2+5x-1=0$
(2) $3x^2+4x-1=0$
(3) $x^2-2x-1=0$
2次方程式を学ぶ↓

文字係数の方程式
(1) $x^2+(a-2)x-2a=0$
(2) $a^2x-a=2ax$
(3) $ax^2-x-a=0$
(1) $x^2+(a-2)x-2a=0$
$(x-2)(x+a)=0$
$x=2,-a$
(2) $a^2x-a=2ax$ より $a(a-2)x=a$
(ア) $a=0$ のとき,この方程式は $0\cdot x=0$
よって,すべての $x$ で成り立つから,解はすべての実数
(イ) $a=2$ のとき,この方程式は $0\cdot x=2$
この式は成り立たないから,解はない
(ウ) $a≠0,2$ のとき $\displaystyle{x=\frac{1}{a-2}}$
(ア)~(ウ) より
(3) $ax^2-x-a=0$
(ア) $a=0$ のとき,この方程式は $-x=0$
これを解くと $x=0$
(イ) $a≠0$ のとき,解の公式より
$\displaystyle{x=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot a\cdot(-a)}}{2a}=\frac{1\pm\sqrt{4a^2+1}}{2a}}$
$4a^2+1>0$ より,これは解として適する
(ア)~(イ) より
文字係数の方程式の解説はこれ↓↓

2次方程式の実数解の個数と判別式
$D>0$ のとき 異なる2つの実数解
$D=0$ のとき 重解(実数解1つ)
$D<0$ のとき 実数解をもたない

ちなみに、判別式 $D=b^2-4ac$ は、
解の公式の $\sqrt{ }$ の中だよ!

(1) 異なる2つの実数解をもつ
(2) 実数解をもたない
(1) 2次方程式 $x^2-3x+k=0$ の判別式を $D$ とすると
$D=(-3)^2-4・1・k=9-4k$
$D>0$ より $9-4k>0$
$\displaystyle{k<\frac{9}{4}}$
(2) $D<0$ より $9-4k<0$
$\displaystyle{k>\frac{9}{4}}$
2次方程式 $x^2-6x+k=0$ の判別式を $D$ とすると
$D=(-6)^2-4・1・k=36-4k$
$D=0$ より $36-4k=0$
$k=9$
このとき $x^2-6x+9=0$
$(x-3)^2=0$
$x=3$
判別式 $D$ を学ぶ↓

2次関数のグラフとx軸
2次関数のグラフとx軸の位置関係
2次関数 $y=ax^2+bx+c$ のグラフと $x$ 軸の共有点の $x$ 座標は、2次方程式 $ax^2+bx+c=0$ の実数解である( $y=0$ を代入)
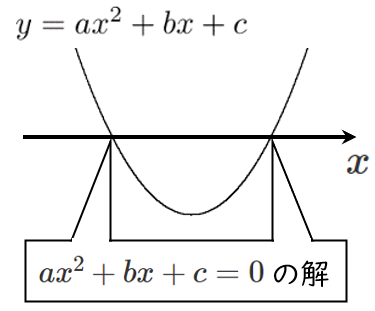
これより、
2次関数 $y=ax^2+bx+c$ のグラフと $x$ 軸の共有点の個数は、2次方程式 $ax^2+bx+c=0$ の実数解の個数と一致する
2次方程式の $ax^2+bx+c=0$ の実数解の個数は、判別式 $D=b^2-4ac$ で判別されるので、2次関数 $y=ax^2+bx+c$ のグラフと $x$ 軸の共有点の個数も判別式 $D$ で判別できる。
2次方程式 $ax^2+bx+c=0$ の判別式を $D$ とすると、2次関数 $y=ax^2+bx+c$ と $x$ 軸の共有点の個数は
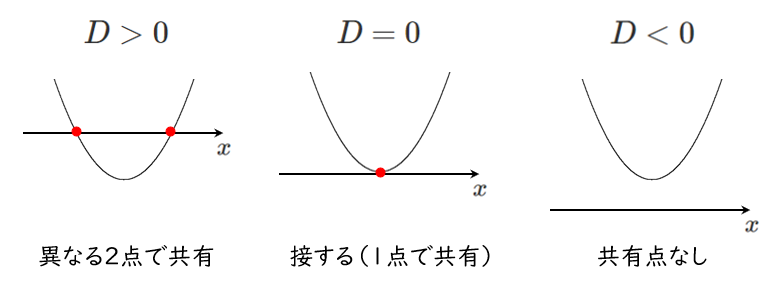
(1) $x$ 軸と異なる2点で交わる
(2) $x$ 軸と交わらない
(1) $y=0$ を代入した2次方程式 $x^2-3x+k=0$ の判別式を $D$ とすると
$D=(-3)^2-4・1・k=9-4k$
$D>0$ より $9-4k>0$
$\displaystyle{k<\frac{9}{4}}$
(2) $D<0$ より $9-4k<0$
$\displaystyle{k>\frac{9}{4}}$
$y=0$ を代入した2次方程式 $x^2-6x+k=0$ の判別式を $D$ とすると
$D=(-6)^2-4・1・k=36-4k$
$D=0$ より $36-4k=0$
$k=9$
このとき $x^2-6x+9=0$
$(x-3)^2=0$
$x=3$
2次関数 $y=ax^2+bx+c$ と $x$ 軸との共有点の個数を調べるのに、判別式 $D$ 以外の方法として、頂点の $y$ 座標を利用する方法もある。
$a>0$ (下に凸)の場合
異なる2点で交わる $ \iff $ (頂点の $y$ 座標)$<0$
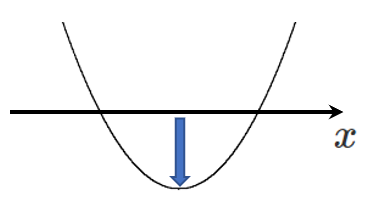
平方完成すると $\displaystyle{y=\left(x-\frac{3}{2}\right)^2-\frac{9}{4}+k}$
頂点は $\displaystyle{\left(\frac{3}{2},-\frac{9}{4}+k\right)}$
異なる2点交わるとき,頂点の $y$ 座標は負なので $\displaystyle{-\frac{9}{4}+k<0}$
これを解いて $\displaystyle{k<\frac{9}{4}}$
2次関数と $x$ 軸の位置関係を学ぶ↓
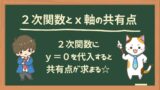

2次関数のグラフと係数の符号
次の図は2次関数 $y=ax^2+bx+c$ のグラフである。このとき,次の値は正,0,負のいずれになるか。
(1) $a$
(2) $b$
(3) $c$
(4) $b^2-4ac$
(5) $a+b+c$
(6) $a-b+c$
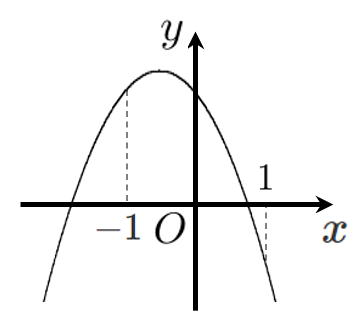
(1) $a$ の正負 ➡ 上に凸か下に凸か
グラフは上に凸なので $a$ は負
(2) $b$ の正負 ➡ 軸 $\displaystyle{x=-\frac{b}{2a}}$ の位置
軸 $\displaystyle{-\frac{b}{2a}}$ は負で $a$ は負なので $b$ は負
(3) $c$ の正負 ➡ $y$ 軸との交点の座標
グラフは $y$ 軸と正の部分で交わるので $c$ は正
(4) $b^2-4ac$ の正負 ➡ グラフと $x$ 軸の共有点の個数
$b^2-4ac$ は判別式 $D$ で、異なる2点で交わっているので $b^2-4ac$ は正
(5) $a+b+c$ の正負 ➡ $x=1$ のときの $y$ 座標
グラフは $x=1$ のとき $x$ 軸より下なので $a+b+c$ は負
(6) $a-b+c$ の正負 ➡ $x=-1$ のときの $y$ 座標
グラフは $x=-1$ のとき $x$ 軸より上なので $a+b+c$ は正
2次関数のグラフと係数の符号を学ぶ↓

2次関数がx軸と切り取る線分の長さ
2次関数 $y=ax^2+bx+c$ ($a>0$)のグラフが異なる2点 $\textrm{A}$、$\textrm{B}$ で交わるとき、$\textrm{A}$、$\textrm{B}$ の座標は $y=0$ を代入して、$ax^2+bx+c=0$ を解くと
$\displaystyle{x=\frac{-b\pm\sqrt{D}}{2a}}$ ただし、$D=b^2-4ac$
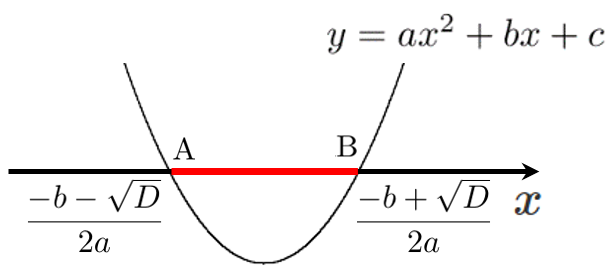
したがって、線分 $\textrm{AB}$ の長さは $\displaystyle{\frac{-b+\sqrt{D}}{2a}-\frac{-b-\sqrt{D}}{2a}=\frac{\sqrt{D}}{a}}$
$a<0$ のときも考慮すると、切り取る線分の長さは $\displaystyle{\frac{\sqrt{D}}{|a|}}$
2次関数 $y=ax^2+bx+c$ のグラフが異なる2点 $\textrm{A}$、$\textrm{B}$ で交わるとき、2次関数が $x$ 軸から切り取る線分の長さは $\displaystyle{\frac{\sqrt{D}}{|a|}}$ ただし、$D=b^2-4ac$
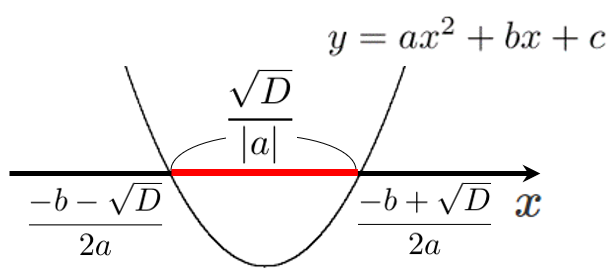
切り取る線分の長さは $\displaystyle{\frac{\sqrt{(-3)^2-4\cdot2\cdot(-3)}}{2}=\frac{\sqrt{33}}{2}}$
2次関数が $x$ 軸から切り取る線分の長さを学ぶ↓
2次不等式

2次不等式はこれをおさえておけば、どんな問題でも解ける!
2次関数のグラフを図示するところから始めよう!
2次不等式の解
(1) $x^2-x-2>0$
(2) $x^2-x-2<0$
(3) $x^2-x-1<0$
(4) $-x^2+2x+1≧0$
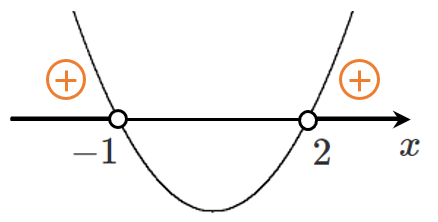
(1) $x^2-x-2>0$
2次関数 $y=x^2-x-2$ のグラフが $x$ 軸より上側( $y>0$ )にある $x$ の値の範囲が解となる
左辺を因数分解して $(x+1)(x-2)>0$
これを解いて $x<-1$,$2<x$
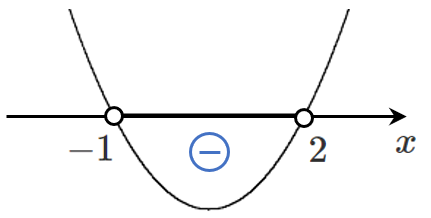
(2) $x^2-x-2<0$
2次関数 $y=x^2-x-2$ のグラフが $x$ 軸より下側( $y<0$ )にある $x$ の値の範囲が解となる
左辺を因数分解して $(x+1)(x-2)<0$
これを解いて $-1<x<2$
(3) $x^2-x-1<0$
$y=x^2-x-1$ と $x$ 軸の共有点を求める
$x^2-x-1=0$ を解くと $\displaystyle{x=\frac{1\pm\sqrt{5}}{2}}$
よって $\displaystyle{\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}}$
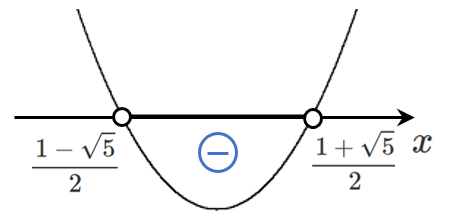
(4) $-x^2+2x+1≧0$
両辺に $-1$ をかけて $x^2-2x-1≦0$
$y=x^2-2x-1$ と $x$ 軸の共有点を求める
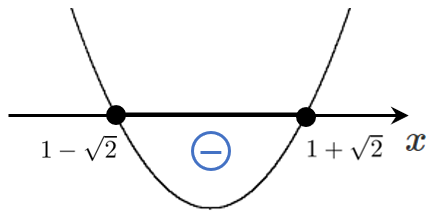
$x^2-2x-1=0$ を解くと $x=1\pm\sqrt{2}$
よって $1-\sqrt{2}≦x≦1+\sqrt{2}$
2次不等式を学ぶ↓



(1) $x^2-4x+4>0$
(2) $x^2-4x+4≧0$
(3) $x^2-4x+4<0$
(4) $x^2-4x+4≦0$
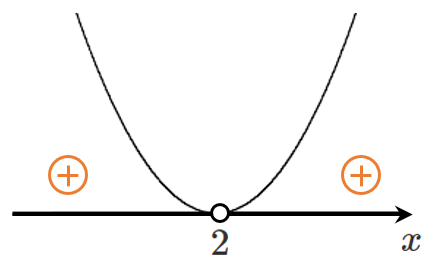
(1) $x^2-4x+4>0$
左辺を因数分解すると $(x-2)^2>0$
これを解くと $x=2$ 以外のすべての実数
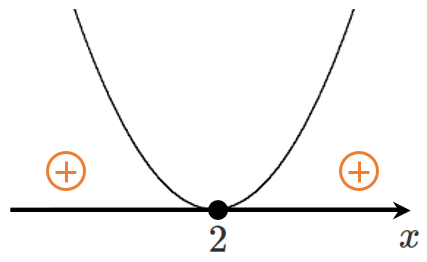
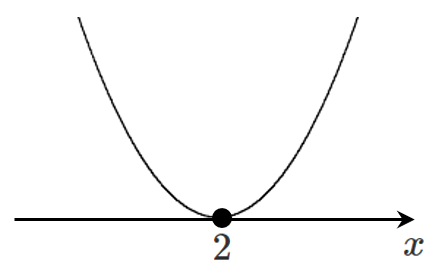
(2) $x^2-4x+4≧0$
左辺を因数分解すると $(x-2)^2≧0$
これを解くと すべての実数
(3) $x^2-4x+4<0$
左辺を因数分解すると $(x-2)^2<0$
これを解くと 解はない
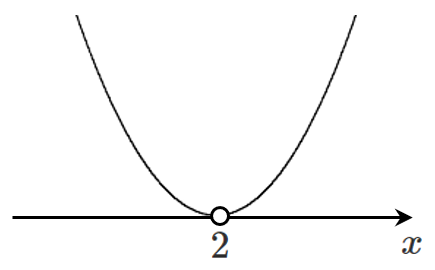
(4) $x^2-4x+4≦0$
左辺を因数分解すると $(x-2)^2≦0$
これを解くと $x=2$
2次不等式を学ぶ↓

(1) $x^2-2x+3>0$
(2) $x^2-2x+3≧0$
(3) $x^2-2x+3<0$
(4) $x^2-2x+3≦0$
2次関数 $y=x^2-2x+3$ について平方完成すると $y=(x-1)^2+2$
頂点は $(1,2)$ より,2次関数 $y=x^2-2x+3$ は $x$ 軸と交わらない
※判別式 $D=(-2)^2-4\cdot1\cdot3=-8<0$ でも $x$ 軸と交わらないことが説明できる
(1) $x^2-2x+3>0$
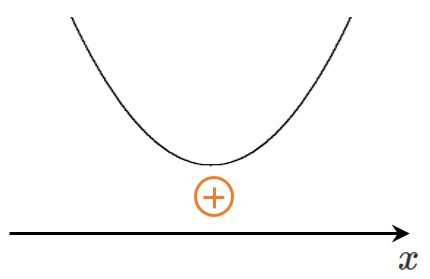
すべての実数
(3) $x^2-2x+3<0$
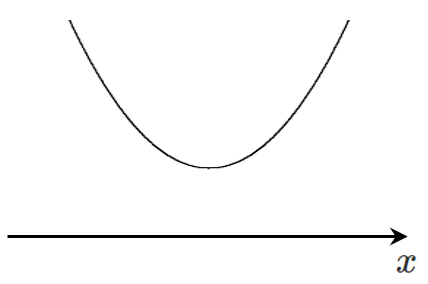
解はない
(2) $x^2-2x+3≧0$

すべての実数
(4) $x^2-2x+3≦0$

解はない
2次不等式を学ぶ↓

絶対不等式
$y=x^2+2kx-3k+4$ とおくと
グラフが $x$ 軸より上側にあるとき
解がすべての実数となる
$x^2+2kx-3k+4=0$ の判別式を $D$ とすると
グラフが $x$ 軸と交わらないので $D<0$
$\displaystyle{\frac{D}{4}=k^2-(-3k+4)=(k-1)(k+4)}$
$D<0$ より $-4<k<1$

$y=(k-2)x^2+2(k-1)x+3k-5$ とおくと
グラフが 下に凸 かつ $x$ 軸より上側にある とき
解がすべての実数となる

下に凸なので $k-2>0$ すなわち $k>2$ … ①
$(k-2)x^2+2(k-1)x+3k-5=0$ の判別式を $D$ とすると
グラフが $x$ 軸と交わらないので $D<0$
$\displaystyle{\frac{D}{4}=(k-1)^2-(k-2)(3k-5)=-2k^2+9k-9=-(2k-3)(k-3)}$
$D<0$ より $-(2k-3)(k-3)<0$ すなわち $(2k-3)(k-3)>0$
これを解いて $\displaystyle{\frac{3}{2}<k<3}$ … ②
①,②の共通範囲をとって $2<k<3$
文字係数の2次不等式
(1) $x^2-(2a+1)x+a^2+a>0$
(2) $x^2-(a+1)x+a<0$
(3) $ax^2-ax-2a>0$
(1) $x^2-(2a+1)x+a^2+a>0$
式変形して $x^2-(2a+1)x+a(a+1)>0$
左辺を因数分解すると $(x-a)\{x-(a+1)\}>0$
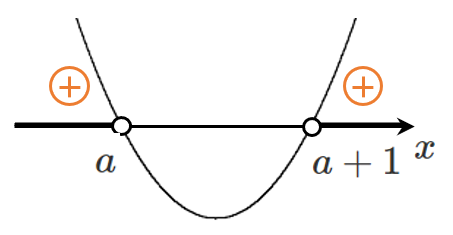
$a<a+1$ より $x<a$,$a+1<x$
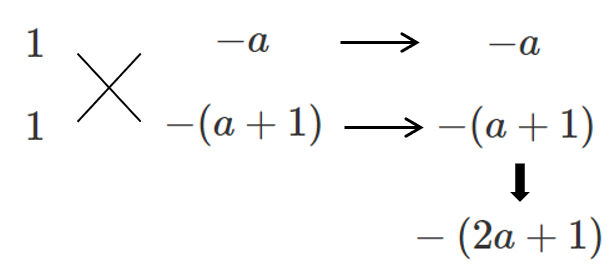
(2) $x^2-(a+1)x+a<0$
左辺を因数分解すると $(x-a)(x-1)<0$ ←$a$ と $1$ の大小関係で場合分け
[1] $a<1$ のとき $a<x<1$
[2] $a=1$ のとき $(x-1)^2<0$ より 解はない
[3] $1<a$ のとき $1<x<a$
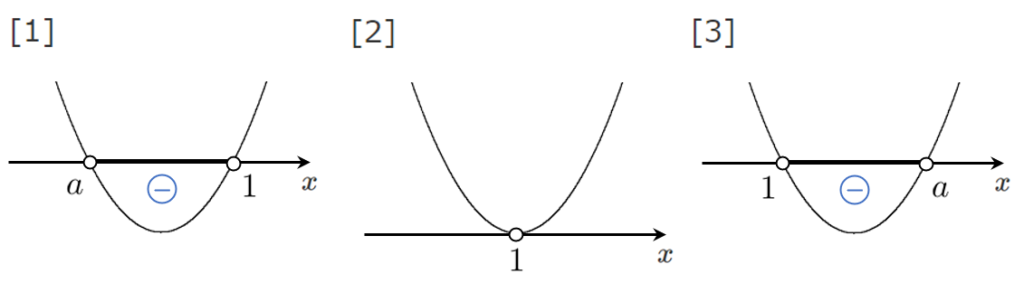
(3) $ax^2-ax-2a>0$
左辺を因数分解すると $a(x^2-x-2)>0$
$a(x+1)(x-2)>0$
[1] $a>0$ のとき $x<-1$,$2<x$
[2] $a=0$ のとき $0>0$ より 解はない
[3] $a<0$ のとき $-1<x<2$
2次方程式の解の存在範囲
異なる2つの正の解・負の解・異符号の解
2次方程式 $f(x)=0$ が異なる2つの正の解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の正の部分と異なる2つの共有点をもつ
[1] $D>0$ ← $x$ 軸と異なる2つの共有点
[2] 軸 $>0$ ← 軸が $x>0$ の部分にある
[3] $f(0)>0$ ← $x=0$ における $y$ 座標が正
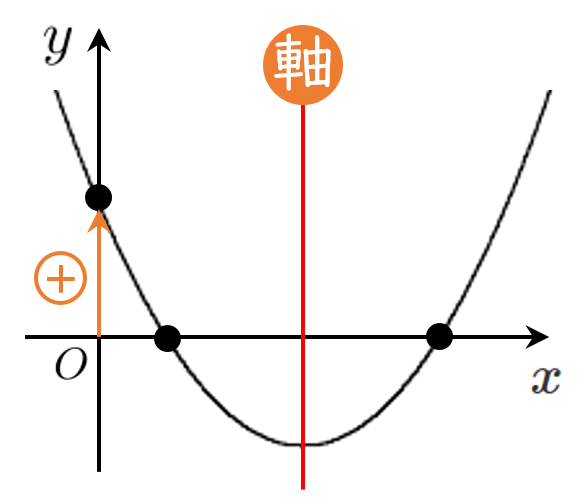
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異なる2つの正の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の正の部分と異なる2つの共有点をもつことである
よって,次の [1]~[3] がすべて成り立つ

[1] $x$ 軸と異なる2つの共有点をもつ
$f(x)=0$ の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=a^2-(-a+2)=(a-1)(a+2)}$
$D>0$ より $a<-2$,$1<a$ … ①
[2] 軸が $x>0$ の部分にある
$y=f(x)$ の軸は直線 $x=a$ であるから $a>0$ … ②
[3] $x=0$ における $y$ 座標が正
$f(0)>0$ であるから $f(0)=-a+2>0$
よって $a<2$ … ③
①~③の共通範囲をとって $1<a<2$
2次方程式 $f(x)=0$ が異なる2つの負の解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の負の部分と異なる2つの共有点をもつ
[1] $D>0$ ← $x$ 軸と異なる2つの共有点
[2] 軸 $<0$ ← 軸が $x<0$ の部分にある
[3] $f(0)>0$ ← $x=0$ における $y$ 座標が正
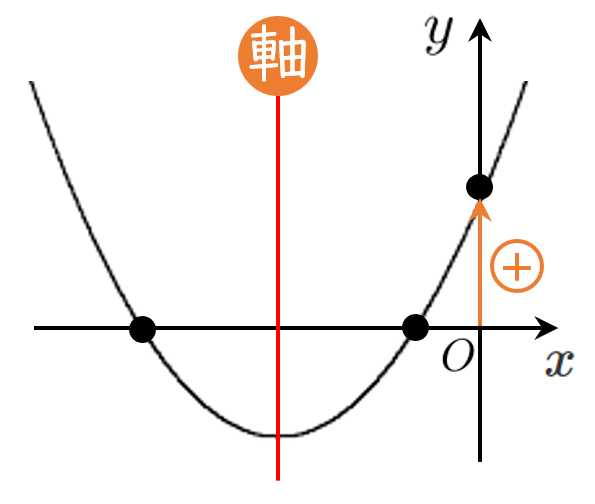

『異なる2つの正の解をもつ条件』と比べると、
軸の条件が違うだけだね!
2次方程式 $f(x)=0$ が符号が異なる2つの解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の正の部分と負の部分で共有点をもつ
[3] $f(0)<0$ ← $x=0$ における $y$ 座標が負
※[1] 判別式 $D>0$ や [2] 軸の条件 は必要ない
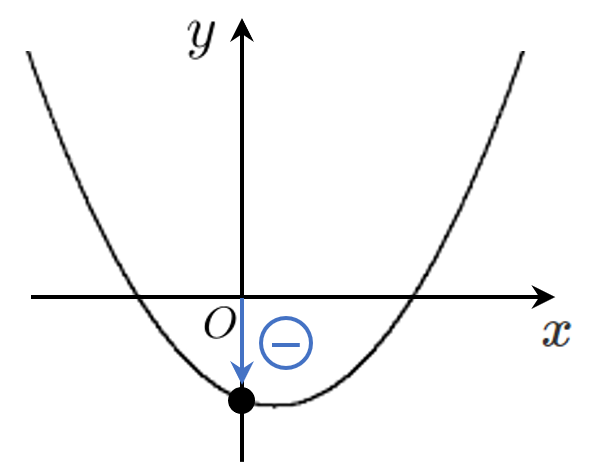
異なる2つの○より大きい・小さい解

例えば、『異なる2つの $1$ より大きい解のときの条件』をみてみよう!
2次方程式 $f(x)=0$ が$1$ より大きい異なる2つの解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の $1$ より大きい部分と異なる2つの共有点をもつ
[1] $D>0$ ← $x$ 軸と異なる2つの共有点
[2] 軸 $>1$ ← 軸が $x>1$ の部分にある
[3] $f(1)>0$ ← $x=1$ における $y$ 座標が正
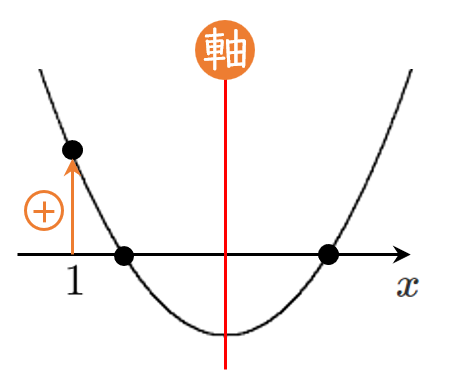

『異なる2つの正の解をもつ条件』と似ているね!
[2] と [3] を少し変えるだけ!

例えば、$2$ より大きい異なる2つの解だったら、
[1] $D>0$ [2] 軸 $>2$ [3] $f(2)>0$
にしたらいいだけ!
2次方程式 $f(x)=0$ が$1$ より大きい解と $1$ より小さい解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の $1$ より大きい部分と小さい部分で共有点をもつ
[3] $f(1)<0$ ← $x=1$ における $y$ 座標が負
※[1] 判別式 $D>0$ や [2] 軸の条件 は必要ない
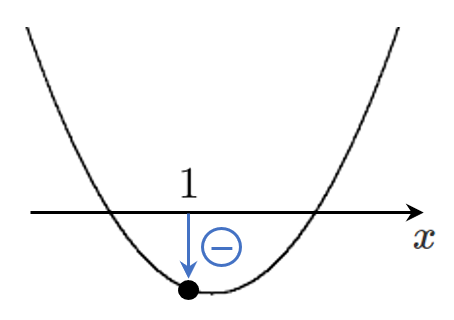

例えば、$2$ より大きい解と $2$ より小さい解だったら、
[3] $f(2)<0$
にしたらいいだけ!
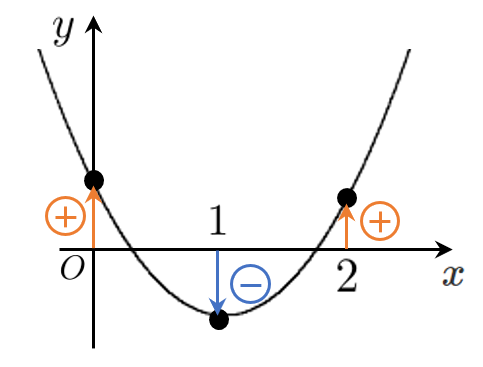
2次方程式 $f(x)=0$ の1つの解が $0$ と $1$ の間に、もう1つの解が $1$ と $2$ の間にある
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸と $0$ と $1$ の間に1つ、$1$ と $2$ の間にもう1つ共有点をもつ
$f(0)>0$ ← $x=0$ における $y$ 座標が正
$f(1)<0$ ← $x=1$ における $y$ 座標が負
$f(2)>0$ ← $x=2$ における $y$ 座標が正

これで『2次関数』の基本はばっちりだね!
共通テストや個別試験に向けた実践的な問題演習を始めよう!

実践的な問題演習には、専属のコーチがいると心強い!
高校数学克服塾MeTa

『高校数学の克服に特化した塾』です!
・完全個別指導で一人ひとりに合わせた数学指導
・解法の暗記ではなく論理的思考力を養って克服を目指す
・学習計画を毎月作成して、勉強方法から改善していく
・いつでも数学の質問ができるLINEサービス(指導がない日でも、いつでも質問できます)
↓↓お申込み・ご相談はこちら↓↓
東大生のオンライン個別指導『トウコベ』

①全ての講師が現役の東大生もしくは東京大学大学院
②完全オンライン型
③圧倒的実績(合格率88%、次の定期テストで22.5点上昇など)
東大生が一対一でお子様に合わせた勉強法を、勉強計画などの実行方法も含めて提案してくれます。
その提案だけでなく、一緒に実行を行ってくれます。
授業だけでなく、家庭学習に関してもサポートが受けられます。
↓↓お申込み・ご相談はこちら↓↓
大学受験ディアロオンライン

大学受験Dialo online(ディアロオンライン)は、Z会グループのノウハウを結集し誕生した大学受験専門のオンライン1:1個別指導塾です。
高品質な「Z会映像教材」と1:1の「合格指導」で無理なく無駄なく難関大合格を目指せる 「完全在宅型」の新しい学びのカタチです。
学習の不明点はSkypeで質問できます。
「わからない」をそのままにせず、スムーズに解決へと導きます。
●合格指導
週1回20分の進捗確認で、毎週の学習スケジュールを合格トレーナーと共有します。
トレーナーは一人ひとりに「今何をすべきか」「次何をすべきか」を提案し、志望校合格に向けての学習を徹底サポート。
この進捗管理を行うことで従来の「通信教育」の弱点を取り除きました。
●Z会の映像見放題
パソコンやスマホ、タブレットで24時間どこからでも映像授業が見放題。
大学入試を知り尽くしたZ会グループの精鋭講師陣が、論理的なアプローチ法から答案の書き方まで徹底解説します。
志望校や現在のレベルに合わせて難易度別に講座をご用意しています。
↓↓お申込み・ご相談はこちら↓↓
他の単元のロードマップもチェック↓


苦手な単元を探して克服しよう↓





コメント