高校数学Ⅱで学ぶ『直線の方程式』を解説!
直線は座標平面の図形において基本中の基本!
「傾き」と「通る点」で直線の方程式を求めることができる!
この投稿を見れば、『直線の方程式』を確実にマスターできます!

直線は基本中の基本!
しっかり学ぼう!
図形と方程式

座標平面上の図形と方程式の関係をみてみよう!
方程式 … 文字が含まれる等式
例えば,$y=x$,$y=x^2$ など
方程式を満たす $x$ と $y$ の組合せを座標平面上にとると図形ができる
$y=x$ を満たすような $x$ と $y$ の組合せを座標で表すと
$(0,0)$,$(1,1)$,$(2,2)$,$(-1,-1)$,$\cdots$
$x$ 座標と $y$ 座標が等しいような点が $y=x$ を満たすような点である
これらを図示すると,座標平面上に直線ができる
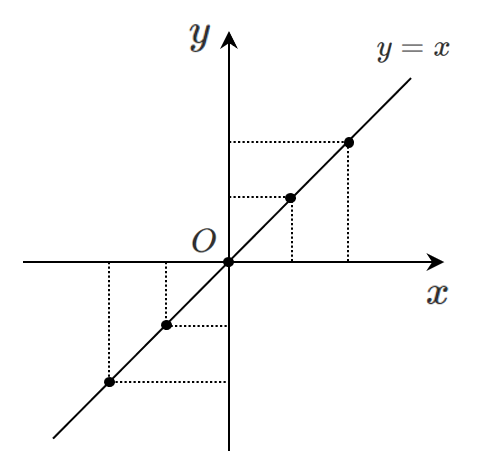
以上より,方程式 $y=x$ は座標平面上では直線を表す
1次関数 $y=ax+b$

中学で習った1次関数を復習しよう!
傾きとは

『傾き』は文字通り,直線がどれくらい傾いているかを表す指標!
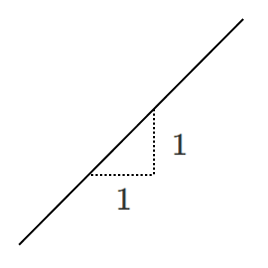
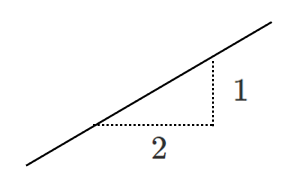
傾き $1$ … $x$ の変化量 $1$,$y$ の変化量 $1$
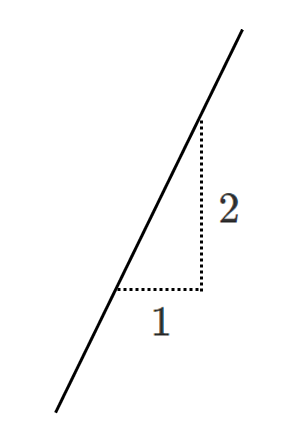
傾き $2$ … $x$ の変化量 $1$,$y$ の変化量 $2$
傾き $\displaystyle{\frac{1}{2}}$ … $x$ の変化量 $2$,$y$ の変化量 $1$
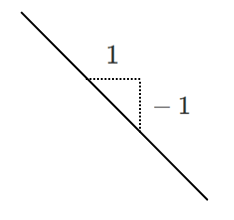
傾き $-1$ … $x$ の変化量 $1$,$y$ の変化量 $-1$
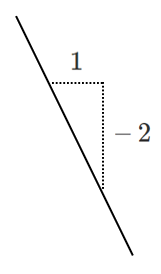
傾き $-2$ … $x$ の変化量 $1$,$y$ の変化量 $-2$
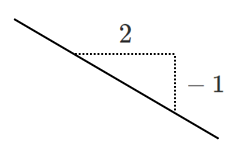
傾き $\displaystyle{-\frac{1}{2}}$ … $x$ の変化量 $2$,$y$ の変化量 $-1$
切片
中学校では,切片といえば $y$ 軸と交わるところ
高校では,これを $y$ 切片という
また,$x$ 軸と交わるところを $x$ 切片という
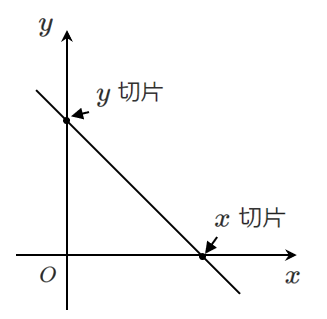
$y=ax+b$ の $b$ が $y$ 切片である理由は
$x=0$ を代入すると $y=b$ となるから

$y=ax+b$ の $b$ が $y$ 切片であることは覚えるだけにならないように!
直線の方程式
傾き $m$,点 $(x_1,y_1)$ を通る直線の方程式は
$y-y_1=m(x-x_1)$
<式の成り立ち>
傾き $m$,$y$ 切片 $b$ である直線の方程式は
$y=mx+b$ … ①
この直線が $(x_1,y_1)$ を通るとき
①に $(x_1,y_1)$ を代入して
$y_1=mx_1+b$ … ②
①-②より, $y-y_1=m(x-x_1)$

この式が表していることは
『傾き』と『通る点』で直線の方程式は求まる
ということ!
傾きと通る点が与えられている問題
$y-(-3)=2(x-1)$
$y=2x-5$
通る2点が与えられている問題

まずは,通る2点の座標から傾きを求める方法!
$\displaystyle{傾き=\frac{yの変化量}{xの変化量}}$ を使おう!
2点 $(○,□)$,$(●,■)$ を通る直線の傾きは
$\displaystyle{\frac{■-□}{●-○}}$

これを使って問題を解こう!
傾きは $\displaystyle{\frac{-2-2}{3-1}=-2}$
傾きが $-2$,点 $(1,2)$ を通る直線の方程式は
$y-2=-2(x-1)$
$y=-2x+4$

『傾き』と『通る点』があれば,直線が求まることを理解しておくことが大切!
まとめ
● 1次関数 $y=ax+b$
傾き $a$,$y$ 切片 $b$ の直線
● 直線の方程式
傾き $m$,点 $(x_1,y_1)$ を通る直線の方程式は
$y-y_1=m(x-x_1)$
『傾き』と『通る点』で直線の方程式は求まる
● 通る2点の座標から傾きを求める方法
2点 $(○,□)$,$(●,■)$ を通る直線の傾きは
$\displaystyle{\frac{■-□}{●-○}}$
問題
(1) 傾き $-1$,点 $(-2,3)$ を通る
(2) 2点 $(-1,2)$,$(1,5)$ を通る
(1) 傾き $-1$,点 $(-2,3)$ を通る
$y-3=-\{x-(-2)\}$ より $y=-x+1$
(2) 2点 $(-1,2)$,$(1,5)$ を通る
傾きは $\displaystyle{\frac{5-2}{1-(-1)}=\frac{3}{2}}$
傾き $\displaystyle{\frac{3}{2}}$,点 $(-1,2)$ を通る直線の方程式は
$\displaystyle{y-2=\frac{3}{2}\{x-(-1)\}}$ より $\displaystyle{y=\frac{3}{2}x+\frac{7}{2}}$

直線の方程式は基本なので,きちんと理解しておこう!




コメント