高校数学Ⅱで習う『相加平均と相乗平均の大小関係』をわかりやすく解説しました!
共通テストや個別学力試験に向けて本格的に数学の勉強を進めていくと、よく登場するのが『相加平均と相乗平均の大小関係』です!
この投稿では、
「相加平均と相乗平均とはそもそもなにか」
「相加平均と相乗平均の大小関係とは」
についてわかりやすく解説しています!
相加平均

$2$ と $8$ の平均はいくつ?

$\displaystyle{\frac{2+8}{2}=5}$

これが相加平均だよ!
相乗平均
ただし,$a>0$,$b>0$
$2$ と $8$ の相乗平均は,$\sqrt{2\cdot8}=\sqrt{16}=4$
$2$ と $8$ をかけた $16$ のかけ算の平均 $4$($4\times4=16$)

相乗平均を図で表すとこんな感じ!
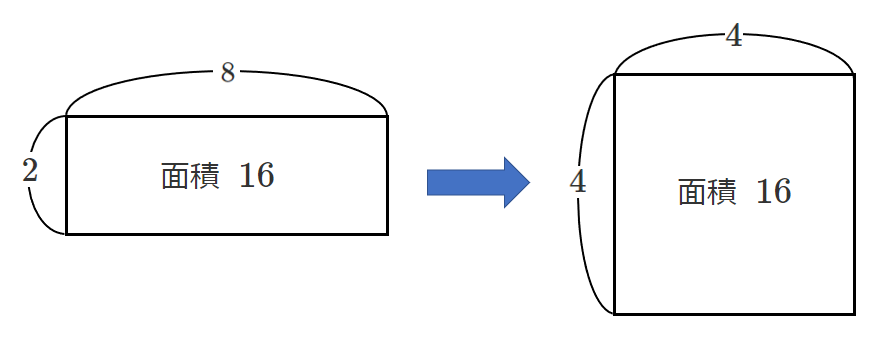
$2$ と $8$ の相乗平均 $4$ は,
$2\times8$ の長方形の面積 $16$ の縦と横の長さを平均化したもの
相乗平均 $\sqrt{ab}$ は $(ab)^\frac{1}{2}$ と表せる

相加平均 $\displaystyle{\frac{a+b}{2}}$ は,足して $\displaystyle{\frac{1}{2}}$ 倍
相乗平均 $\sqrt{ab}$ は,かけて $\displaystyle{\frac{1}{2}}$ 乗

$\sqrt{ }$ の中に負の数は入れないからね!
相加平均と相乗平均の大小関係

$2$ と $8$ の相加平均と相乗平均の大小関係を調べてみよう!

相加平均が $\displaystyle{\frac{2+8}{2}=5}$
相乗平均が $\sqrt{2\cdot8}=4$
(相加平均)>(相乗平均) の関係になってそう!

他の数の組合せを試しても同じことが言えるよ!
○ $3$ と $5$ の相加平均と相乗平均
相加平均が $\displaystyle{\frac{3+5}{2}=4}$
相乗平均が $\sqrt{3\cdot5}=\sqrt{15}$
$4^2>(\sqrt{15})^2$ より,$4>\sqrt{15}$
(相加平均)>(相乗平均)

$4$ と $4$ の相加平均と相乗平均はどうかな?

相加平均が $\displaystyle{\frac{4+4}{2}=4}$
相乗平均が $\sqrt{4\cdot4}=4$
(相加平均)=(相乗平均) になる!

同じ数のときは,(相加平均)=(相乗平均) になるね!
ともに正である $a$ と $b$ の相加平均と相乗平均について,
$a≠b$ のとき,(相加平均)>(相乗平均)
$a=b$ のとき,(相加平均)=(相乗平均)
以上より,相加平均と相乗平均の大小関係は
(相加平均)≧(相乗平均)
すなわち, $\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$
等号が成り立つ(相加平均と相乗平均が等しい)のは,$a=b$ のとき
$a>0$,$b>0$ のとき, $\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$
等号が成り立つのは,$a=b$ のとき
証明
$\displaystyle{\frac{a+b}{2}-\sqrt{ab}}$
$\displaystyle{=\frac{(\sqrt{a})^2+(\sqrt{b})^2}{2}-\frac{2\sqrt{ab}}{2}}$
$\displaystyle{=\frac{(\sqrt{a})^2-2\sqrt{ab}+(\sqrt{b})^2}{2}}$
$\displaystyle{=\frac{(\sqrt{a}-\sqrt{b})^2}{2}≧0}$
よって, $\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$ が成り立つ
等号成立は, $\sqrt{a}-\sqrt{b}=0$
すなわち, $a=b$ のとき
まとめ
● 相加平均
$a$ と $b$ の相加平均は $\displaystyle{\frac{a+b}{2}}$
相加平均は,足して $\displaystyle{\frac{1}{2}}$ 倍
● 相乗平均
ともに正である $a$ と $b$ の相乗平均は $\sqrt{ab}=(ab)^\frac{1}{2}$
相乗平均は,かけて $\displaystyle{\frac{1}{2}}$ 乗
● 相加平均と相乗平均の大小関係
(相加平均)≧(相乗平均)
$a>0$,$b>0$ のとき, $\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$
等号が成り立つ(相加平均と相乗平均が等しい)のは,$a=b$ のとき

相加平均と相乗平均の大小関係が分からなくなったら,適当な数で大小関係を考えたら思い出せるよ!




コメント