2次不等式の解が「すべての実数」や「解はない」となる問題
あなたも苦手ではないでしょうか?
2次不等式は『2次関数を用いて解く』という鉄則を理解しておけば,
どんな2次不等式でも必ず解くことができる!
2次関数がx軸と接する場合の2次不等式について考えてみましょう!

2次不等式の基本を復習しよう!
2次不等式は「2次関数を使って解く」ことがポイントだよ!

2次関数が接する場合の2次不等式
2次関数 $y=x^2-2x+1$ とおく
$y=0$ を代入すると
$x^2-2x+1=0$
$(x-1)^2=0$
$x=1$
2次関数 $y=x^2-2x+1$ は $x$ 軸と接する
2次不等式 $x^2-2x+1<0$ を解くには
$y<0$ すなわち $x$ 軸より下側( $x$ 軸上を含まない)
に2次関数がある $x$ の範囲を求める
$y<0$ を満たす $x$ の範囲を求めると
解はない
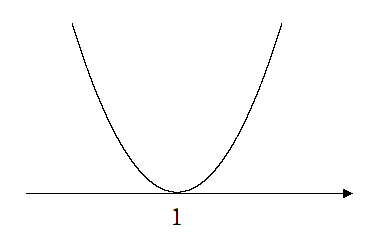

2次関数は $x$ 軸より下側にはないから「解はない」になるよ!
2次関数 $y=x^2-2x+1$ とおく
2次不等式 $x^2-2x+1≦0$ を解くには
$y≦0$ すなわち $x$ 軸より下側( $x$ 軸上も含む)
に2次関数がある $x$ の範囲を求める
$y≦0$ を満たす $x$ の範囲を求めると
$x=1$
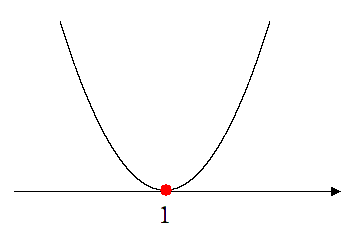

$x$ 軸上にある $x=1$ だけが解になるよ!
2次関数 $y=x^2-2x+1$ とおく
2次不等式 $x^2-2x+1>0$ を解くには
$y>0$ すなわち $x$ 軸より上側( $x$ 軸上を含まない)
に2次関数がある $x$ の範囲を求める
$y>0$ を満たす $x$ の範囲を求めると
$x=1$ 以外のすべての実数
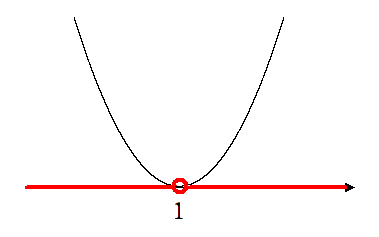

$x=1$ は $x$ 軸上にあるから「 $x=1$ 以外」になるよ!
2次関数 $y=x^2-2x+1$ とおく
2次不等式 $x^2-2x+1≧0$ を解くには
$y≧0$ すなわち $x$ 軸より上側( $x$ 軸上も含む)
に2次関数がある $x$ の範囲を求める
$y≧0$ を満たす $x$ の範囲を求めると
すべての実数
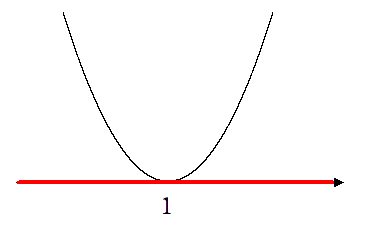

図を描いて、$x$ 軸より上か下か、$x$ 軸上を含むか含まないかを考えれば、解を求めることができるよ!
まとめ
$y=(x-a)^2$ は $x=a$ で $x$ 軸と接する
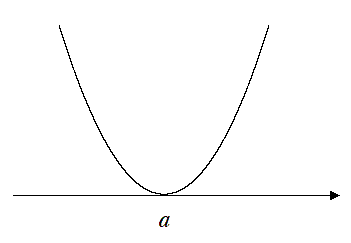
●$(x-a)^2<0$
$x$ 軸より下側( $x$ 軸上を含まない)なので
「解はない」
●$(x-a)^2≦0$
$x$ 軸より下側( $x$ 軸上も含む)なので
「$x=a$」
●$(x-a)^2>0$
$x$ 軸より上側( $x$ 軸上を含まない)なので
「 $x=a$ 以外のすべての実数」
●$(x-a)^2≧0$
$x$ 軸より上側( $x$ 軸上も含む)なので
「すべての実数」
問題
問題 次の2次不等式を解け。
(1) $x^2-4x+4<0$
(2) $x^2-4x+4≦0$
(3) $x^2-4x+4>0$
(4) $x^2-4x+4≧0$
解答
(1) $x^2-4x+4<0$
2次関数 $y=x^2-4x+4$ とおく
$y=0$ を代入すると
$x^2-4x+4=0$
$(x-2)^2=0$
$x=2$
2次関数 $y=x^2-4x+4$ は $x$ 軸と接する
2次不等式 $x^2-4x+4<0$ を解くには
$y<0$ すなわち $x$ 軸より下側( $x$ 軸上を含まない)
に2次関数がある $x$ の範囲を求める
$y<0$ を満たす $x$ の範囲を求めると
解はない
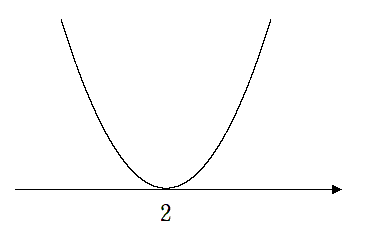
(2) $x^2-4x+4≦0$
2次関数 $y=x^2-4x+4$ とおく
2次不等式 $x^2-4x+4≦0$ を解くには
$y≦0$ すなわち $x$ 軸より下側( $x$ 軸上も含む)
に2次関数がある $x$ の範囲を求める
$y≦0$ を満たす $x$ の範囲を求めると
$x=2$
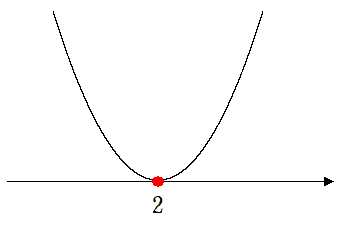
(3) $x^2-4x+4>0$
2次関数 $y=x^2-4x+4$ とおく
2次不等式 $x^2-4x+4>0$ を解くには
$y>0$ すなわち $x$ 軸より上側( $x$ 軸上を含まない)
に2次関数がある $x$ の範囲を求める
$y>0$ を満たす $x$ の範囲を求めると
$x=2$ 以外のすべての実数
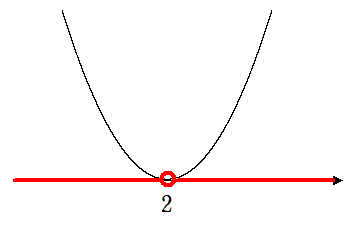
(4) $x^2-4x+4≧0$
2次関数 $y=x^2-4x+4$ とおく
2次不等式 $x^2-4x+4≧0$ を解くには
$y≧0$ すなわち $x$ 軸より上側( $x$ 軸上も含む)
に2次関数がある $x$ の範囲を求める
$y≧0$ を満たす $x$ の範囲を求めると
すべての実数
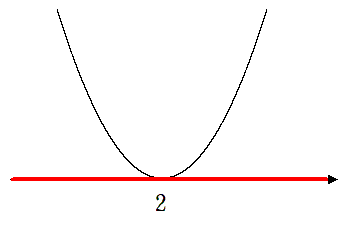

2次関数と $x$ 軸の位置関係を表した図を描くことが大切だね!
🔰平方完成|x²の係数が1以外の場合
🔰定義域における最大・最小
🔰基本形と一般形の利用
🔰2次方程式の実数解の個数と判別式
🔰2次関数のグラフとx軸の位置関係
🔰2次不等式|解の公式
🔰2次不等式|交わらない
🔰2次不等式|x²の係数が負
🔵絶対不等式
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント