ド・モルガンの法則は理解できていますか?
『ド・モルガンの法則がなぜその式になるのか』
集合を使ってわかりやすく説明します!
式を覚えているだけはNG!
どんな場面で使えばいいのか?
と悩んでいる人もこの投稿で解決します!
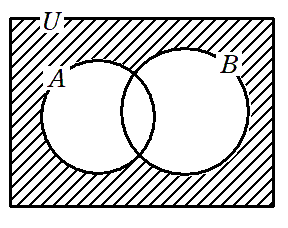
集合の基本

集合の基本である
共通部分(かつ)・和集合(または)・補集合
を復習しよう!
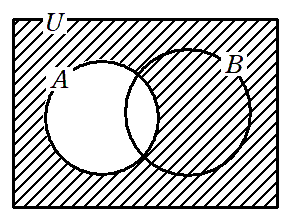
$\overline{A}∩\overline{B}$

$\overline{A}∩\overline{B}$ を書き換えてみよう!
$\overline{A}$( $A$ の外)
$\overline{B}$( $B$ の外)
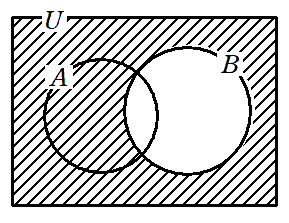
$\overline{A}∩\overline{B}$( $A$ の外 かつ $B$ の外 )
この集合は $A∪B$ の外になります
すなわち,$\overline{A∪B}$
よって,
$\overline{A}∩\overline{B}=\overline{A∪B}$
$\overline{A}∪\overline{B}$

$\overline{A}∪\overline{B}$ を書き換えてみよう!
$\overline{A}$( $A$ の外)

$\overline{B}$( $B$ の外)

$\overline{A}∪\overline{B}$( $A$ の外 または $B$ の外 )
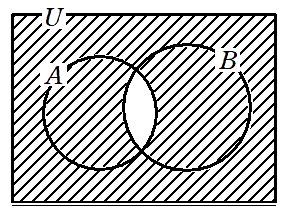
この集合は $A∩B$ の外になります
すなわち,$\overline{A∩B}$
よって,
$\overline{A}∪\overline{B}=\overline{A∩B}$
ド・モルガンの法則
$\overline{A}∩\overline{B}$( $A$ の外 かつ $B$ の外 )
を考えるよりも
$\overline{A∪B}$( $A∪B$ の外 )
を考える方が簡単
同様に
$\overline{A}∪\overline{B}$( $A$ の外 または $B$ の外 )
を考えるよりも
$\overline{A∩B}$( $A∩B$ の外 )
を考える方が簡単
$\overline{A}∩\overline{B}$ や $\overline{A}∪\overline{B}$ を考えるときは
ド・モルガンの法則で $\overline{A∪B}$ や $\overline{A∩B}$ に書き換えて考えましょう
まとめ
ド・モルガンの法則
● $\overline{A}∩\overline{B}=\overline{A∪B}$
● $\overline{A}∪\overline{B}=\overline{A∩B}$
問題
$10$ 以下の自然数全体の集合を全体集合 $U$,$6$ の正の約数全体の集合を $A$,$10$ 以下の素数全体の集合を $B$ とする。次の集合を求めよ。
(1) $\overline{A}∩\overline{B}$
(2) $\overline{A}∪\overline{B}$
解答
$A=\{1,2,3,6\}$
$B=\{2,3,5,7\}$
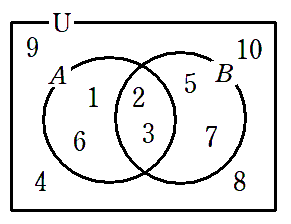
(1) $\overline{A}∩\overline{B}$
ド・モルガンの法則より
$\overline{A}∩\overline{B}=\overline{A∪B}$
$\overline{A∪B}=\{4,8,9,10\}$ なので
$\overline{A}∩\overline{B}=\{4,8,9,10\}$
(2) $\overline{A}∪\overline{B}$
ド・モルガンの法則より
$\overline{A}∪\overline{B}=\overline{A∩B}$
$\overline{A∩B}=\{1,4,5,6,7,8,9,10\}$ なので
$\overline{A}∪\overline{B}=\{1,4,5,6,7,8,9,10\}$

ド・モルガンの法則は他にも使う場面があるので、きちんと覚えておこう!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント