ベクトルが表す点の存在範囲②

ベクトルが表す点の存在範囲

１　　$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$s+t=1$

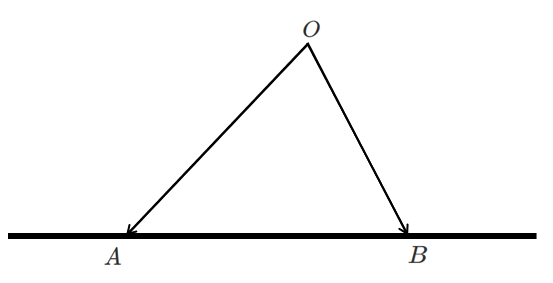
点 $P$ は直線 $AB$ 上

　

２　　$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$s≧0，t≧0，s+t=1$

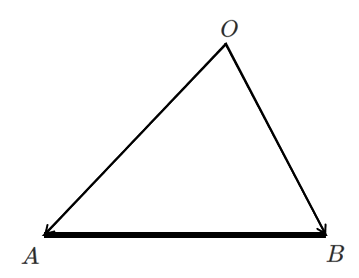
点 $P$ は線分 $AB$ 上

　

３　　$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$s≧0，t≧0，s+t≦1$

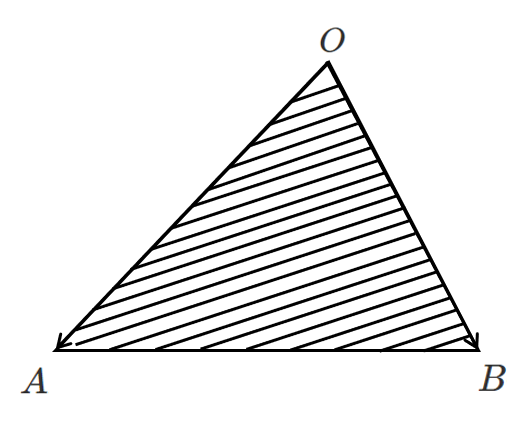
点 $P$ は$\triangle OAB$ の周および内部

　

４　　$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　　$0≦s≦1，0≦t≦1$　

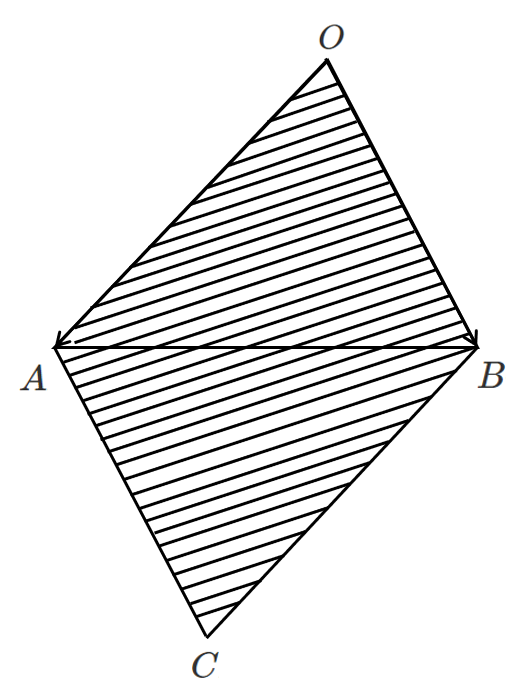
点 $P$ は平行四辺形 $OACB$ の周および内部

ただし，点 $C$ は $\overrightarrow{OA}=\overrightarrow{BC}$ を満たす点

　

１と２の存在範囲について，詳しくはこれ↓

ベクトルが表す点の存在範囲①

直線ABまたは線分AB上に点Pが存在するときのベクトルの式を理解して問題で活用しよう！

enjoy-mathematics.com

2022.12.17

　

△OAB の周および内部

３　　$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$s≧0，t≧0，s+t≦1$

点 $P$ は$\triangle OAB$ の周および内部

$\displaystyle{s+t=\frac{1}{2}}$ より

$2s+2t=1$

$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ より

$\displaystyle{\overrightarrow{OP}=2s\left(\frac{1}{2}\overrightarrow{OA}\right)+2t\left(\frac{1}{2}\overrightarrow{OB}\right)}$

$2s=s’$，$2t=t’$，$\displaystyle{\frac{1}{2}\overrightarrow{OA}=\overrightarrow{OC}}$， $\displaystyle{\frac{1}{2}\overrightarrow{OB}=\overrightarrow{OD}}$ とすると

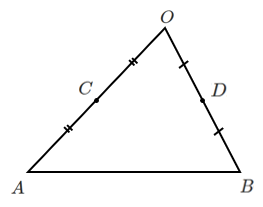
$\overrightarrow{OP}=s’\overrightarrow{OC}+t’\overrightarrow{OD}$

$s’≧0，t’≧0，s’+t’=1$

簡単に表すと

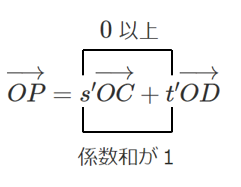
したがって，

点 $P$ は線分 $CD$ 上

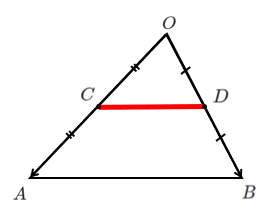
同様に考えて

$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$\displaystyle{s≧0，t≧0，s+t=\frac{1}{3}}$

を図示すると

$\displaystyle{\overrightarrow{OP}=3s\left(\frac{1}{3}\overrightarrow{OA}\right)+3t\left(\frac{1}{3}\overrightarrow{OB}\right)}$　　$s≧0，t≧0，3s+3t=1$

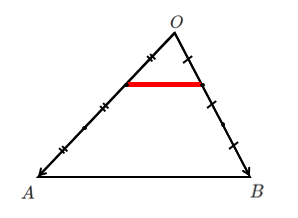
辺 $OA$ と辺 $OB$ を三等分した点を結ぶ線分になる

以上より

$\displaystyle{\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}}$　　$s≧0，t≧0，s+t≦1$

において，$s+t≦1$ には

$\displaystyle{s+t=\frac{1}{2}}$

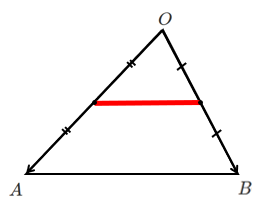
や

$\displaystyle{s+t=\frac{1}{3}}$ が含まれている

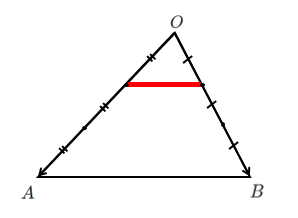
つまり

$s+t≦1$ を満たすような線分を集めると

$\triangle OAB$ の周および内部

となる

平行四辺形 $OACB$ の周および内部

４　　$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　　$0≦s≦1，0≦t≦1$　

点 $P$ は平行四辺形 $OACB$ の周および内部

ただし，点 $C$ は $\overrightarrow{OA}=\overrightarrow{BC}$ を満たす点

ベクトルの和

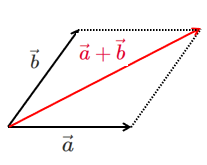
を利用する

$s\overrightarrow{OA}$　$0≦s≦1$　とは

$\overrightarrow{OA}$ と向きが等しく， $\overrightarrow{OA}$ より大きさが小さいベクトル

同様に

$t\overrightarrow{OB}$　$0≦t≦1$　とは

$\overrightarrow{OB}$ と向きが等しく， $\overrightarrow{OB}$ より大きさが小さいベクトル

$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　　$0≦s≦1，0≦t≦1$　

を満たす $\overrightarrow{OP}$ の集まりを図示してみると

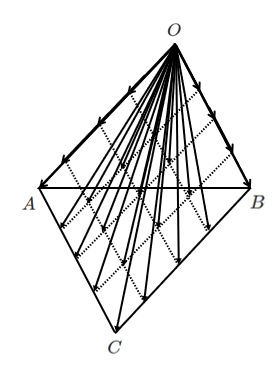
平行四辺形の内部に点 $P$ が集まることが分かる

問題

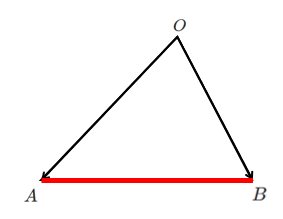
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$\displaystyle{s≧0，t≧0，s+t=1}$

を満たす点 $P$ の存在範囲は，線分 $AB$ 上

$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$\displaystyle{s≧0，t≧0，s+t=2}$

を満たす点 $P$ の存在範囲を求めると

$s+t=2$ より

$\displaystyle{\frac{1}{2}s+\frac{1}{2}t=1}$

$\displaystyle{\overrightarrow{OP}=\frac{1}{2}s\left(2\overrightarrow{OA}\right)+\frac{1}{2}t\left(\overrightarrow{OB}\right)}$

$\displaystyle{\frac{1}{2}s=s’}$，$ \displaystyle{\frac{1}{2}t=t’}$，$2\overrightarrow{OA}=\overrightarrow{OC}$， $2\overrightarrow{OB}=\overrightarrow{OD}$ とすると

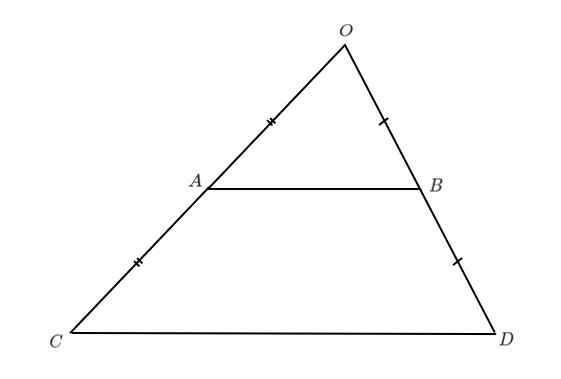
$\overrightarrow{OP}=s’\overrightarrow{OC}+t’\overrightarrow{OD}$

$s’≧0，t’≧0，s’+t’=1$

簡単に表すと

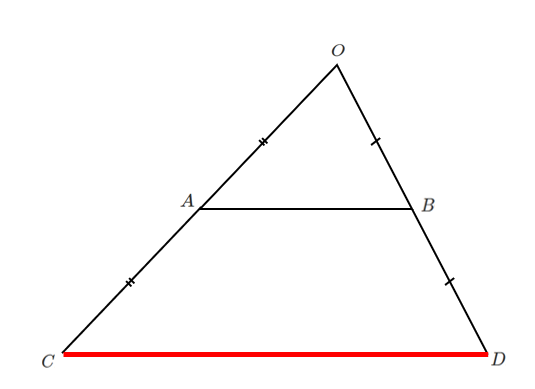
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$\displaystyle{s≧0，t≧0，s+t=2}$

を満たす点 $P$ の存在範囲は，線分 $CD$ 上

以上より

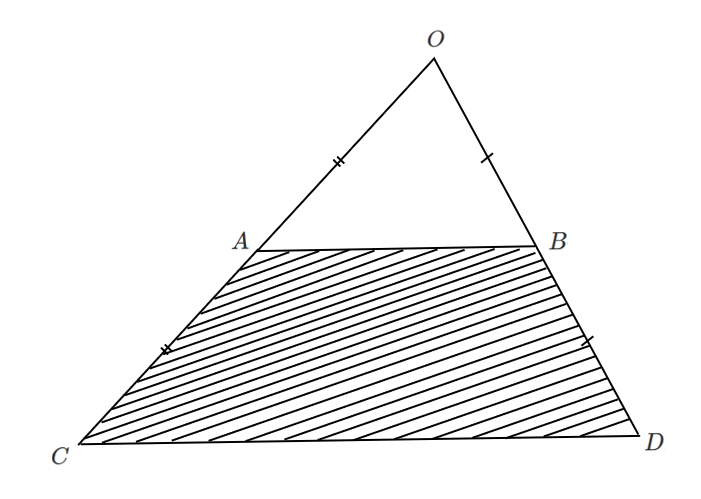
$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$\displaystyle{s≧0，t≧0，1≦s+t≦2}$

を満たす点 $P$ の存在範囲は以下の斜線部となる

＜別解＞

$s+t=k$ とすると

$\displaystyle{\frac{s}{k}+\frac{t}{k}=1}$

$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$ より

$\displaystyle{\overrightarrow{OP}=\frac{s}{k}\left(k\overrightarrow{OA}\right)+\frac{t}{k}\left(k\overrightarrow{OB}\right)}$

$\displaystyle{\frac{s}{k}=s’}$，$ \displaystyle{\frac{t}{k}=t’}$，$k\overrightarrow{OA}=\overrightarrow{OQ}$， $k\overrightarrow{OB}=\overrightarrow{OR}$ とすると

$\overrightarrow{OP}=s’\overrightarrow{OQ}+t’\overrightarrow{OR}$

$s’≧0，t’≧0，s’+t’=1$

となり，点 $P$ は線分 $QR$ 上に存在する

ここで，$2\overrightarrow{OA}=\overrightarrow{OC}$， $2\overrightarrow{OB}=\overrightarrow{OD}$ を満たす点 $C$ と $D$ をとるとき

$1≦k≦2$ より，点 $Q$ と 点 $R$ はそれぞれ線分 $AC$，$BD$ 上にある

したがって，点 $P$ の存在範囲は以下の斜線部となる

まとめ

● $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　$s≧0，t≧0，s+t≦1$

点 $P$ は$\triangle OAB$ の周および内部

　

● $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}$　　　$0≦s≦1，0≦t≦1$　

点 $P$ は平行四辺形 $OACB$ の周および内部

ただし，点 $C$ は $\overrightarrow{OA}=\overrightarrow{BC}$ を満たす点