
メネラウスの定理が苦手な人は多いよね!
メネラウスの定理の使い方を学ぼう!
メネラウスの定理
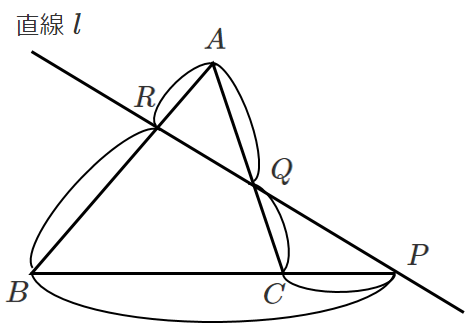
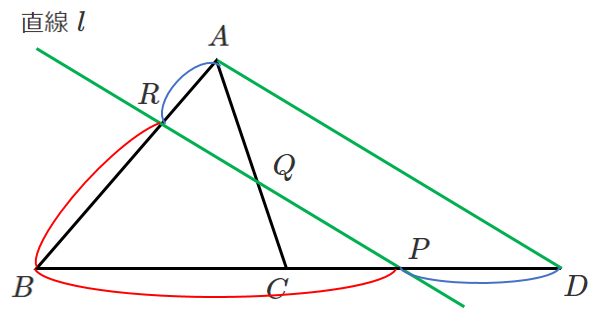
$\triangle ABC$ の辺 $BC$,$CA$,$AB$ またはその延長が,三角形の頂点を通らない直線 $l$ と,それぞれ $P$,$Q$,$R$ で交わるとき
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1}$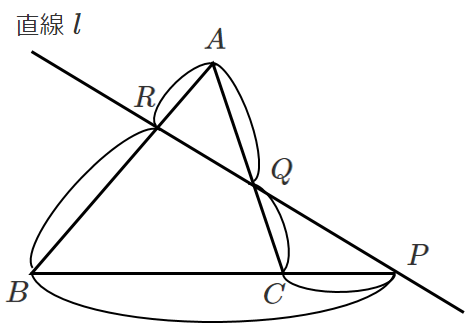

メネラウスの定理もチェバの定理と同じように一筆書きで一周!
チェバの定理の復習はこれ↓


チェバの定理の一筆書きは分かりやすかったけど,メネラウスの定理の一筆書きは複雑だよ~

確かに複雑だよね!
もう少しメネラウスの定理について詳しく見てみよう!
三角形と直線に着目
メネラウスの定理は「三角形」と「直線」によってできる図形に用いられる定理
三角形の辺または三角形の辺の延長と直線の交点を『分点』とすると
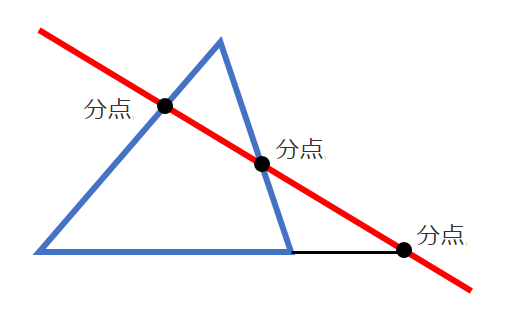
三角形の3辺の間または延長にそれぞれ1点ずつ『分点』がとれる
(辺の間にできる点が辺の内分点,辺の延長にできる点が辺の外分点)
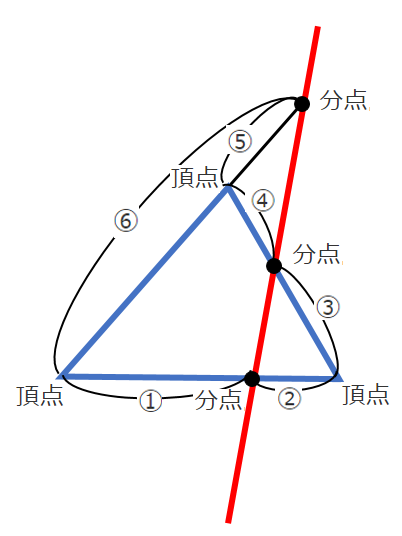
メネラウスの定理は,
三角形の頂点(どこでもよい)からスタートして,
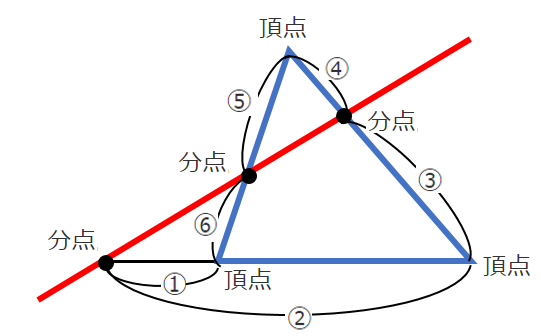
頂点→分点→頂点→分点→頂点→分点→頂点
の順に一筆書きで作ることができる
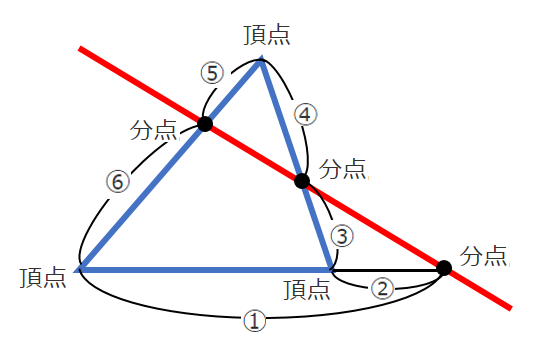
$\displaystyle{\frac{①}{②}・\frac{③}{④}・\frac{⑤}{⑥}=1}$

「三角形」と「直線」を意識して,頂点→分点→頂点の順に一筆書き!
メネラウスの定理の証明
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1}$ を証明する
[証明]
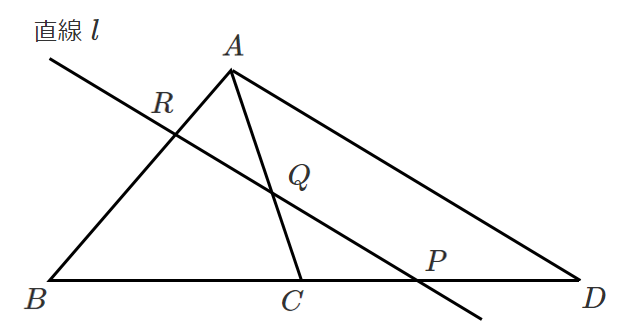
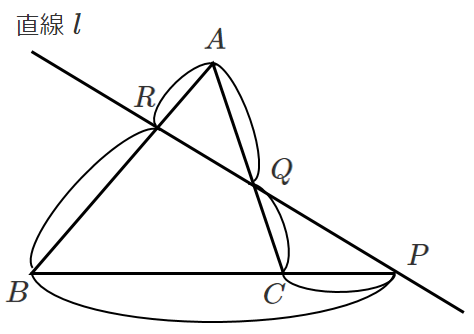
頂点 $A$ を通り,直線 $l$ に平行な直線を引き直線 $BC$ との交点を $D$ とすると
$\displaystyle{\frac{CQ}{QA}=\frac{CP}{PD}}$
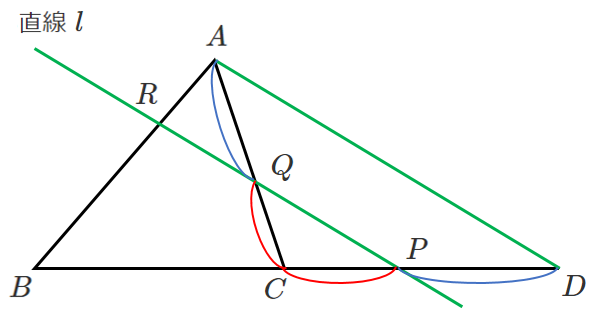
$\displaystyle{\frac{AR}{RB}=\frac{DP}{PB}}$
よって
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=\frac{BP}{PC}・\frac{CP}{PD}・\frac{DP}{PB}=1}$
まとめ
● メネラウスの定理
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1}$
「三角形」と「直線」に着目して,頂点→分点→頂点の順に一筆書き
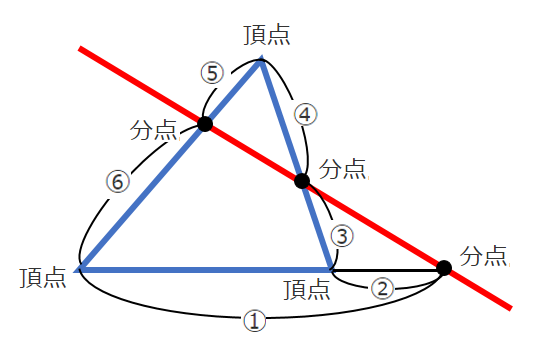
$\displaystyle{\frac{①}{②}・\frac{③}{④}・\frac{⑤}{⑥}=1}$
問題
(1) $CQ:QA$
(2) $PQ:QR$
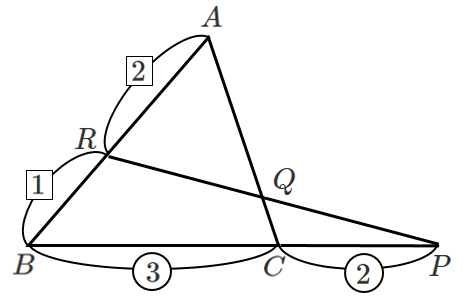
(1) $CQ:QA$
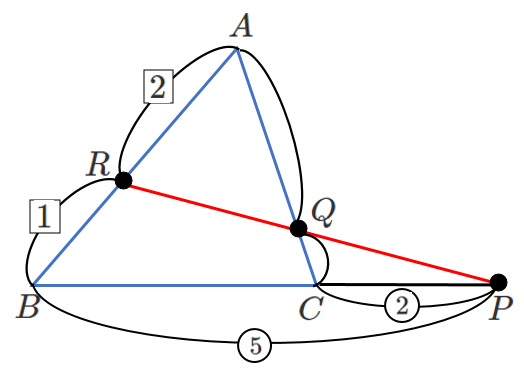
メネラウスの定理より
$\displaystyle{\frac{CQ}{QA}・\frac{2}{1}・\frac{5}{2}=1}$
$\displaystyle{\frac{CQ}{QA}・\frac{5}{1}=1}$
$\displaystyle{\frac{CQ}{QA}=\frac{1}{5}}$
よって $CQ:QA=1:5$
(2) $PQ:QR$
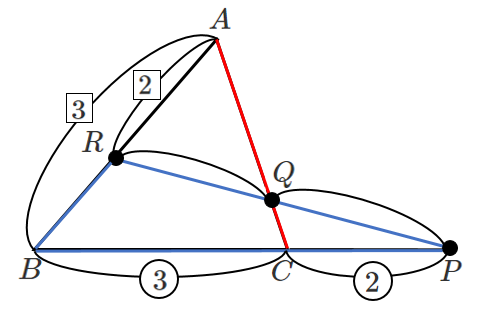
メネラウスの定理より
$\displaystyle{\frac{PQ}{QR}・\frac{2}{3}・\frac{3}{2}=1}$
$\displaystyle{\frac{CQ}{QA}・\frac{1}{1}=1}$
$\displaystyle{\frac{CQ}{QA}=\frac{1}{1}}$
よって $CQ:QA=1:1$

チェバの定理と同様,メネラウスの定理もよく出題されるので,しっかり練習しよう!




コメント