高校数学Ⅱの【三角関数】で学ぶ『三角関数の合成を用いる方程式』について解説!
三角関数の合成を用いる方程式は,模試でも頻出の問題!
この投稿を見て,確実に解けるように練習しよう!
三角関数の合成

三角関数の合成の復習をしよう!
$a\sin\theta+b\cos\theta$ の合成
- 点 $(a,b)$ をとる
- $r$ と $\alpha$ を求める
- $r\sin(\theta+\alpha)$ に式変形する
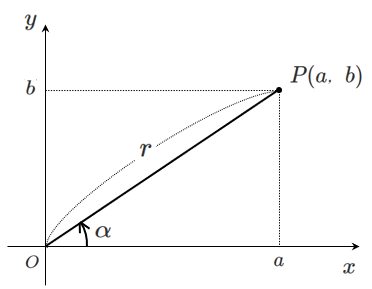
「三角関数の合成」詳しくはこれ↓

三角関数の合成を用いる方程式

「三角関数の合成」と「置き換え」を上手く使いながら,方程式を解こう!
左辺の $\sqrt{3}\sin\theta-\cos\theta$ を合成すると
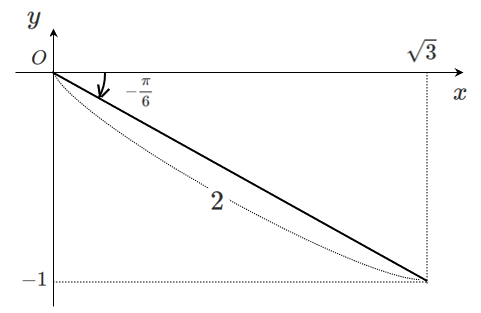
$\displaystyle{\sqrt{3}\sin\theta-\cos\theta=2\sin\left(\theta-\frac{\pi}{6}\right)}$
よって
$\sqrt{3}\sin\theta-\cos\theta=1$
$\displaystyle{2\sin\left(\theta-\frac{\pi}{6}\right)=1}$
$\displaystyle{\sin\left(\theta-\frac{\pi}{6}\right)=\frac{1}{2}}$
$\displaystyle{\theta-\frac{\pi}{6}=t}$ とすると
$\displaystyle{\sin t=\frac{1}{2}}$
$0≦\theta<2\pi$ より
$0≦\theta<2\pi$
$\displaystyle{0-\frac{\pi}{6}≦\theta-\frac{\pi}{6}<2\pi-\frac{\pi}{6}}$
$\displaystyle{-\frac{\pi}{6}≦\theta-\frac{\pi}{6}<\frac{11}{6}\pi}$
$\displaystyle{-\frac{\pi}{6}≦t<\frac{11}{6}\pi}$
よって
$\displaystyle{\sin t=\frac{1}{2} \left(-\frac{\pi}{6}≦t<\frac{11}{6}\pi\right)}$
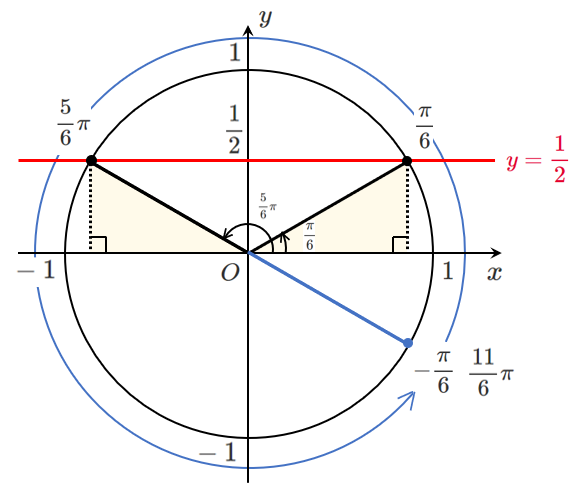
$\displaystyle{-\frac{\pi}{6}≦t<\frac{11}{6}\pi}$ の範囲で $\displaystyle{\sin t=\frac{1}{2}}$ を解くと
$\displaystyle{t=\frac{\pi}{6},\frac{5}{6}\pi}$
$\displaystyle{\theta-\frac{\pi}{6}=\frac{\pi}{6},\frac{5}{6}\pi}$
よって
$\displaystyle{\theta-\frac{\pi}{6}=\frac{\pi}{6}}$ より $\displaystyle{\theta=\frac{\pi}{3}}$
$\displaystyle{\theta-\frac{\pi}{6}=\frac{5}{6}\pi}$ より $\theta=\pi$
したがって
$\displaystyle{\theta=\frac{\pi}{3},\pi}$

「置き換え」をして解くことが大切!
次の問題は間違えやすいので注意!
左辺の $\sin\theta+\sqrt{3}\cos\theta$ を合成すると
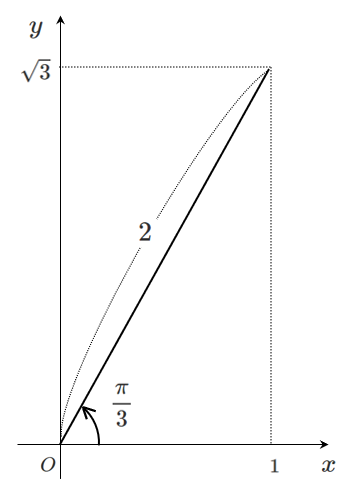
$\displaystyle{\sin\theta+\sqrt{3}\cos\theta=2\sin\left(\theta+\frac{\pi}{3}\right)}$
よって
$ \sin\theta+\sqrt{3}\cos\theta=1$
$\displaystyle{2\sin\left(\theta+\frac{\pi}{3}\right)=1}$
$\displaystyle{\sin\left(\theta+\frac{\pi}{3}\right)=\frac{1}{2}}$
$\displaystyle{\theta+\frac{\pi}{3}=t}$ とすると
$\displaystyle{\sin t=\frac{1}{2}}$
$0≦\theta<2\pi$ より
$0≦\theta<2\pi$
$\displaystyle{0+\frac{\pi}{3}≦\theta+\frac{\pi}{3}<2\pi+\frac{\pi}{3}}$
$\displaystyle{\frac{\pi}{3}≦\theta+\frac{\pi}{3}<\frac{7}{3}\pi}$
$\displaystyle{\frac{\pi}{3}≦t<\frac{7}{3}\pi}$
よって
$\displaystyle{\sin t=\frac{1}{2} \left(\frac{\pi}{3}≦t<\frac{7}{3}\pi\right)}$
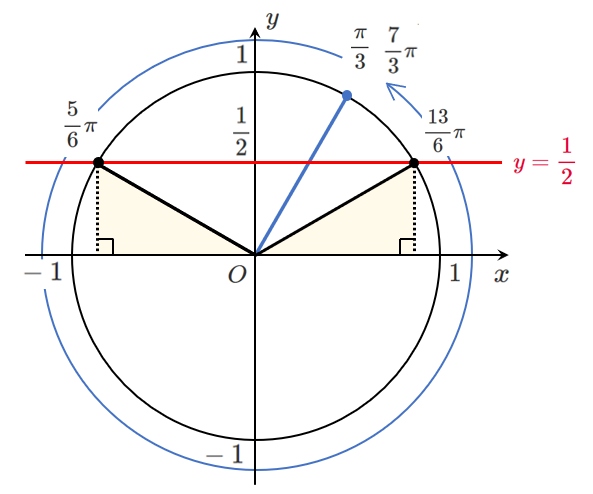
$\displaystyle{\frac{\pi}{3}≦t<\frac{7}{3}\pi}$ の範囲で $\displaystyle{\sin t=\frac{1}{2}}$ を解くと
$\displaystyle{t=\frac{5}{6}\pi,\frac{13}{6}\pi}$
$\displaystyle{\theta+\frac{\pi}{3}=\frac{5}{6}\pi,\frac{13}{6}\pi}$
よって
$\displaystyle{\theta+\frac{\pi}{3}=\frac{5}{6}\pi}$ より $\displaystyle{\theta=\frac{\pi}{2}}$
$\displaystyle{\theta+\frac{\pi}{3}=\frac{13}{6}\pi}$ より $\displaystyle{\theta=\frac{11}{6}\pi}$
したがって
$\displaystyle{\theta=\frac{\pi}{2},\frac{11}{6}\pi}$
<NGの解答>
$\displaystyle{\sin t=\frac{1}{2} \left(\frac{\pi}{3}≦t<\frac{7}{3}\pi\right)}$
$\displaystyle{t=\frac{\pi}{6},\frac{5}{6}\pi}$
$\displaystyle{\frac{\pi}{3}≦t<\frac{7}{3}\pi}$ の範囲に $\displaystyle{\frac{\pi}{6}}$ が存在しないので×

置き換えた文字 $t$ の範囲を意識して,方程式を解くようにしよう!
問題
$0≦\theta<2\pi$ のとき,次の方程式を解け。
(1) $\displaystyle{\sin\theta+\cos\theta=\frac{1}{\sqrt{2}}}$
(2) $\sin\theta-\sqrt{3}\cos\theta=-1$
(1) $\displaystyle{\sin\theta+\cos\theta=\frac{1}{\sqrt{2}}}$
左辺の $\sin\theta+\cos\theta $ を合成すると
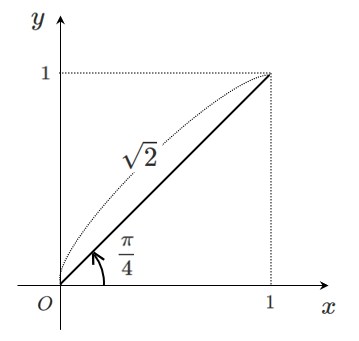
$\displaystyle{\sin\theta+\cos\theta=\sqrt{2}\sin\left(\theta+\frac{\pi}{4}\right)}$
よって
$\displaystyle{\sin\theta+\cos\theta=\frac{1}{\sqrt{2}}}$
$\displaystyle{\sqrt{2}\sin\left(\theta+\frac{\pi}{4}\right)=\frac{1}{\sqrt{2}}}$
$\displaystyle{\sin\left(\theta+\frac{\pi}{4}\right)=\frac{1}{2}}$
$\displaystyle{\theta+\frac{\pi}{4}=t}$ とすると
$\displaystyle{\sin t=\frac{1}{2}}$
$0≦\theta<2\pi$ より
$0≦\theta<2\pi$
$\displaystyle{0+\frac{\pi}{4}≦\theta+\frac{\pi}{4}<2\pi+\frac{\pi}{4}}$
$\displaystyle{\frac{\pi}{4}≦\theta+\frac{\pi}{4}<\frac{9}{4}\pi}$
$\displaystyle{\frac{\pi}{4}≦t<\frac{9}{4}\pi}$
よって
$\displaystyle{\sin t=\frac{1}{2} \left(\frac{\pi}{4}≦t<\frac{9}{4}\pi\right)}$
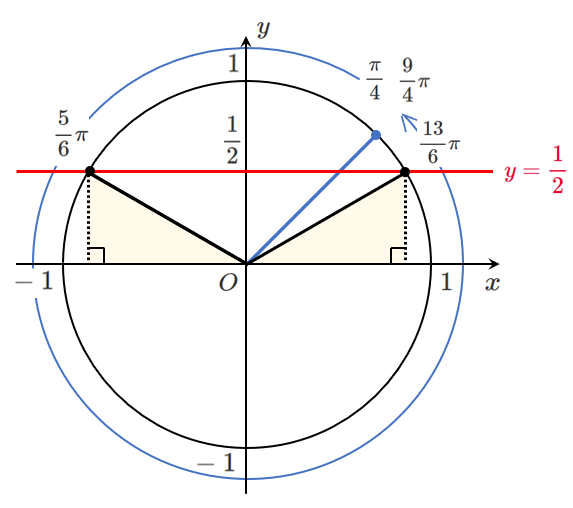
$\displaystyle{\frac{\pi}{4}≦t<\frac{9}{4}\pi}$ の範囲で $\displaystyle{\sin t=\frac{1}{2}}$ を解くと
$\displaystyle{t=\frac{5}{6}\pi,\frac{13}{6}\pi}$
$\displaystyle{\theta+\frac{\pi}{4}=\frac{5}{6}\pi,\frac{13}{6}\pi}$
よって
$\displaystyle{\theta+\frac{\pi}{4}=\frac{5}{6}\pi}$ より $\displaystyle{\theta=\frac{7}{12}\pi}$
$\displaystyle{\theta+\frac{\pi}{4}=\frac{13}{6}\pi}$ より $\displaystyle{\theta=\frac{23}{12}\pi}$
したがって
$\displaystyle{\theta=\frac{7}{12}\pi,\frac{23}{12}\pi}$
(2) $\sin\theta-\sqrt{3}\cos\theta=-1$
左辺の $\sin\theta-\sqrt{3}\cos\theta $ を合成すると
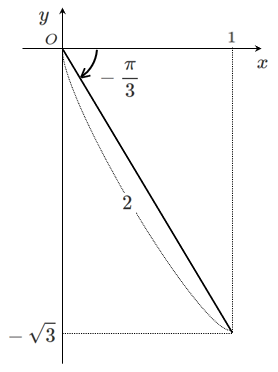
$\displaystyle{\sin\theta-\sqrt{3}\cos\theta=2\sin\left(\theta-\frac{\pi}{3}\right)}$
よって
$\sin\theta-\sqrt{3}\cos\theta=-1$
$\displaystyle{2\sin\left(\theta-\frac{\pi}{3}\right)=-1}$
$\displaystyle{\sin\left(\theta-\frac{\pi}{3}\right)=-\frac{1}{2}}$
$\displaystyle{\theta-\frac{\pi}{3}=t}$ とすると
$\displaystyle{\sin t=-\frac{1}{2}}$
$0≦\theta<2\pi$ より
$0≦\theta<2\pi$
$\displaystyle{0-\frac{\pi}{3}≦\theta-\frac{\pi}{3}<2\pi-\frac{\pi}{3}}$
$\displaystyle{-\frac{\pi}{3}≦\theta-\frac{\pi}{3}<\frac{5}{3}\pi}$
$\displaystyle{-\frac{\pi}{3}≦t<\frac{5}{3}\pi}$
よって
$\displaystyle{\sin t=-\frac{1}{2} \left(-\frac{\pi}{3}≦t<\frac{5}{3}\pi\right)}$
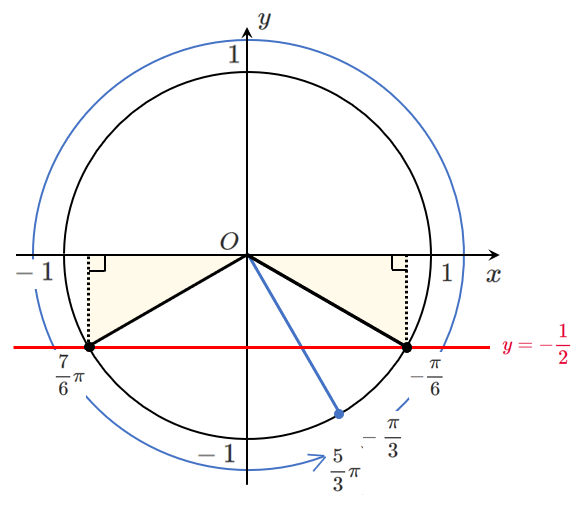
$\displaystyle{-\frac{\pi}{3}≦t<\frac{5}{3}\pi}$ の範囲で $\displaystyle{\sin t=-\frac{1}{2}}$ を解くと
$\displaystyle{t=-\frac{\pi}{6},\frac{7}{6}\pi}$
$\displaystyle{\theta-\frac{\pi}{3}=-\frac{\pi}{6},\frac{7}{6}\pi}$
よって
$\displaystyle{\theta-\frac{\pi}{3}=-\frac{\pi}{6}}$ より $\displaystyle{\theta=\frac{\pi}{6}}$
$\displaystyle{\theta-\frac{\pi}{3}=\frac{7}{6}\pi}$ より $\displaystyle{\theta=\frac{3}{2}\pi}$
したがって
$\displaystyle{\theta=\frac{\pi}{6},\frac{3}{2}\pi}$
まとめ
● 三角関数の合成を用いる方程式
$a\sin\theta+b\cos\theta$ を $r\sin(\theta+\alpha)$ に式変形する
$\theta+\alpha$ を $t$ で置き換える
$t$ の範囲を踏まえて,方程式を満たす $t$ を求める
$t$ を $\theta+\alpha$ に戻す

慣れないうちは,置き換えをして解くのがコツ!




コメント