高校数学Ⅱの【三角関数】で学ぶ『三角関数の最大・最小(相互関係・2倍角の公式)』について解説!
三角関数の最大・最小に関する問題は,模試でも頻出の重要問題!
この投稿を見て,確実に解けるように練習しよう!
三角関数の相互関係と2倍角の公式
今回の問題で使う公式は,以下の2種類!
三角関数の相互関係
● $\sin^2\theta+\cos^2\theta=1$
この公式を使えば$\cos^2\theta=1-\sin^2\theta$ より,$\cos^2\theta$ を $\sin^2\theta$ で表せる
$\sin^2\theta=1-\cos^2\theta$ より,$\sin^2\theta$ を $\cos^2\theta$ で表せる
三角関数の2倍角の公式
● $\cos2\theta=1-2\sin^2\theta$ → $\cos2\theta$ を $\sin^2\theta$ で表せる
● $\cos2\theta=2\cos^2\theta-1$ → $\cos2\theta$ を $\cos^2\theta$ で表せる
解法の手順
「三角関数の最大・最小(相互関係・2倍角の公式)」の解法の手順
(手順1) 相互関係・2倍角の公式を利用して,関数 $y$ を $\sin\theta$ または $\cos\theta$ だけの式にする
(手順2) $\sin\theta$ または $\cos\theta$ を $t$ と置き換える
(手順3) $\theta$ の範囲から $t$ の範囲を求める
(手順4) $t$ の範囲において,関数 $y$ の最大・最小,そのときの $t$ の値を求める
(手順5) $t$ を $\theta$ にもどす
(手順2) $\sin\theta$ または $\cos\theta$ を $t$ と置き換える
(手順3) $\theta$ の範囲から $t$ の範囲を求める
(手順4) $t$ の範囲において,関数 $y$ の最大・最小,そのときの $t$ の値を求める
(手順5) $t$ を $\theta$ にもどす
問題
問題
次の関数の最大値,最小値を求めよ。また,そのときの $\theta$ の値を求めよ。
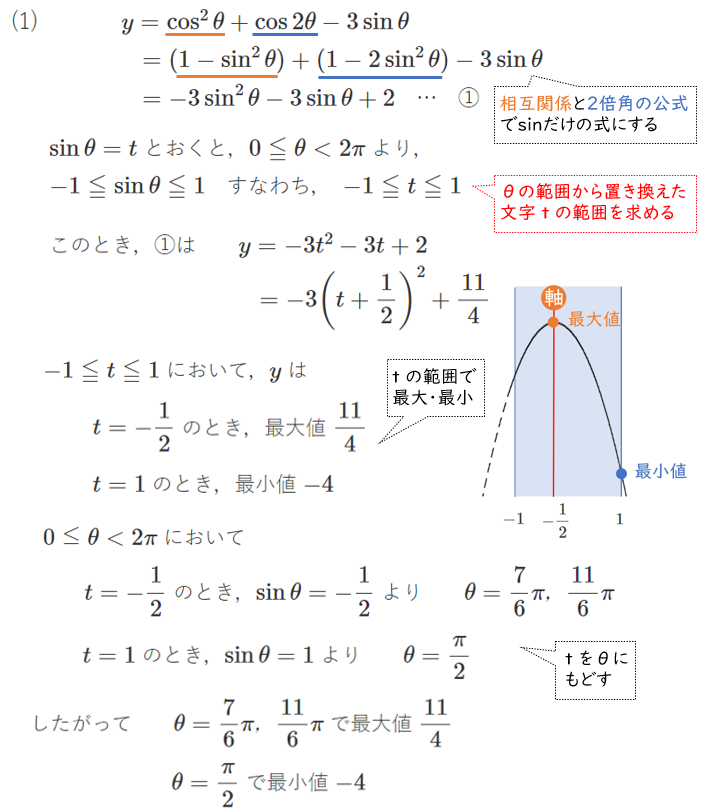
(1) $y=\cos^2\theta+\cos2\theta-3\sin\theta$ $(0≦\theta<2\pi)$
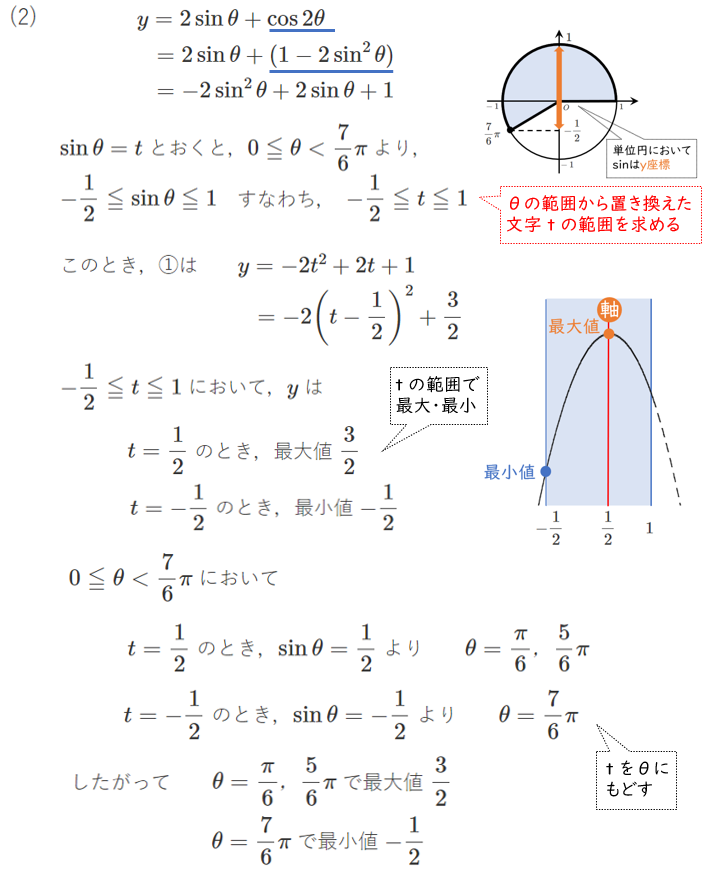
(2) $y=2\sin\theta+\cos2\theta$ $\displaystyle{\left(0≦\theta<\frac{7}{6}\pi\right)}$
(1) $y=\cos^2\theta+\cos2\theta-3\sin\theta$ $(0≦\theta<2\pi)$
(2) $y=2\sin\theta+\cos2\theta$ $\displaystyle{\left(0≦\theta<\frac{7}{6}\pi\right)}$
解答




コメント