高校数学Ⅱの【三角関数】で学ぶ『三角関数を含む方程式』について解説!
三角関数の中でも基本中の基本である方程式を完璧に理解しよう!
この投稿を見れば,『三角関数を含む方程式』はバッチリ!

三角関数の基本!
三角関数を含む方程式を解こう!
三角関数の定義
座標平面上において原点を中心とする半径 $r$ の円をかき,
下図のように点 $P(x,y)$ ,角 $\theta$ をとる
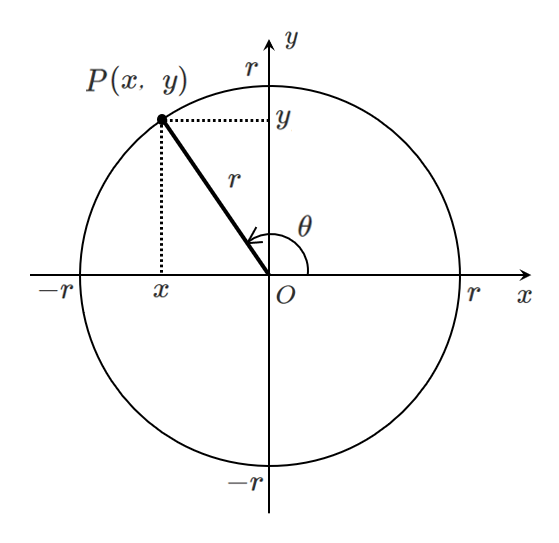
単位円を用いた三角関数
$\sin\theta$ と $\cos\theta$
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r}$$
$$ \Downarrow r=1とする$$
$$\sin\theta=y,\cos\theta=x$$
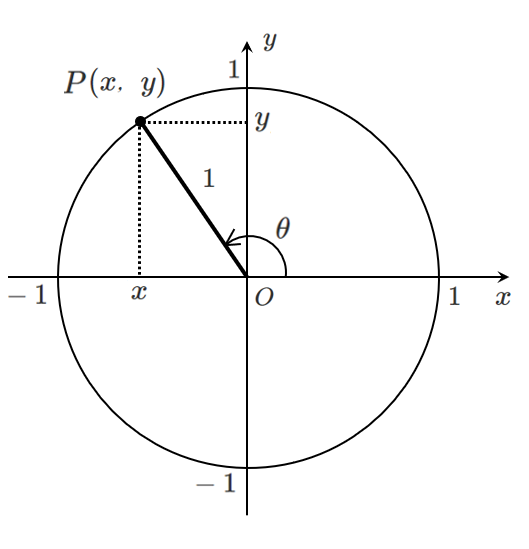
$\tan\theta$
$$\displaystyle{\tan\theta=\frac{y}{x}}$$
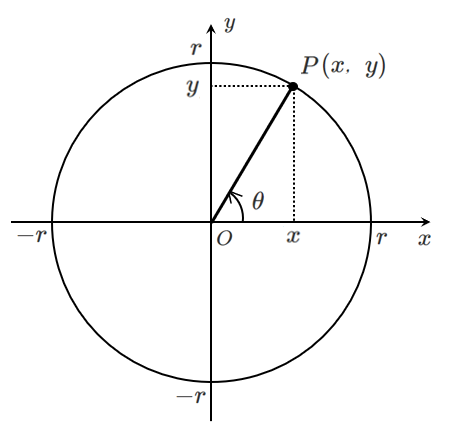
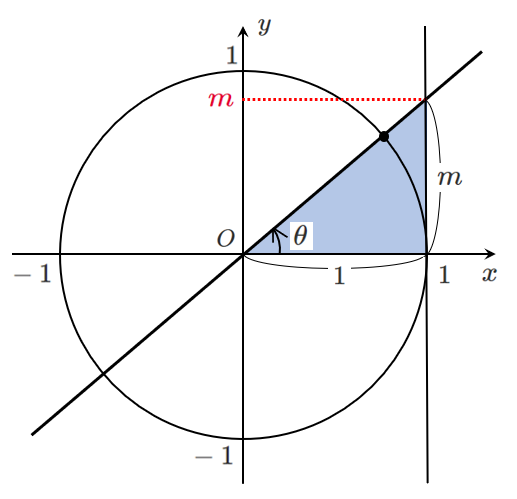
直線 $OP$ の傾きが $\displaystyle{\frac{y}{x}}$
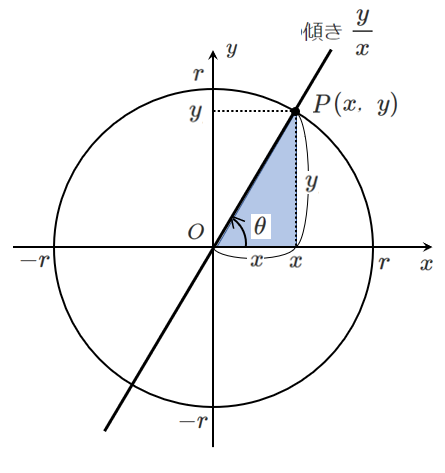
$\tan\theta$ は傾き
$\tan\theta$ の値は傾きを表しているので,以下のように考える
$$\tan\theta=m$$
三角関数を含む方程式
$\sin$ は $y$ 座標
$\cos$ は $x$ 座標
$\tan$ は 傾き
$\sin$

「$\sin$ は $y$ 座標」を用いて方程式を解こう!
単位円における $y$ 座標が $\displaystyle{\frac{1}{2}}$ の点を求めると
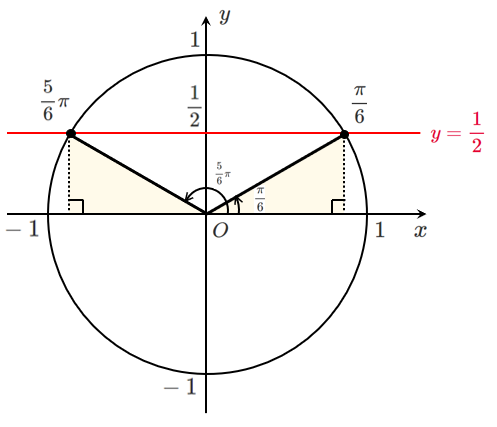
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{6},\frac{5}{6}\pi}$

$0≦\theta<2\pi$ というのは,「1周で」という意味!

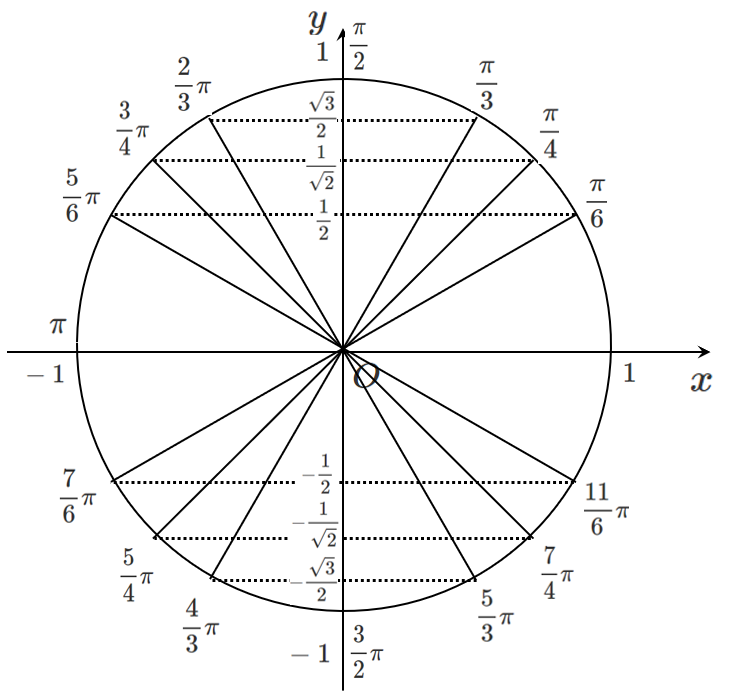
単位円で $\sin\theta$ の値を考えると下のような図になる!
$\cos$

「$\cos$ は $x$ 座標」を用いて方程式を解こう!
単位円における $x$ 座標が $\displaystyle{-\frac{1}{2}}$ の点を求めると
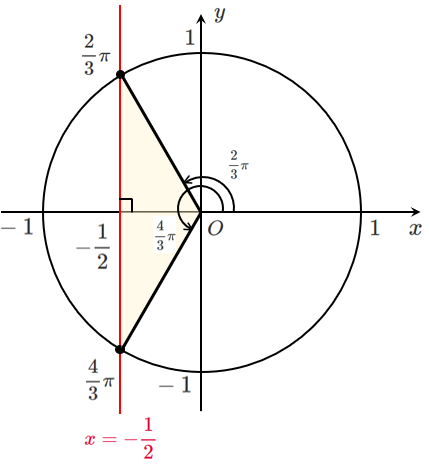
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{2}{3}\pi,\frac{4}{3}\pi}$

単位円で $\cos\theta$ の値を考えると下のような図になる!
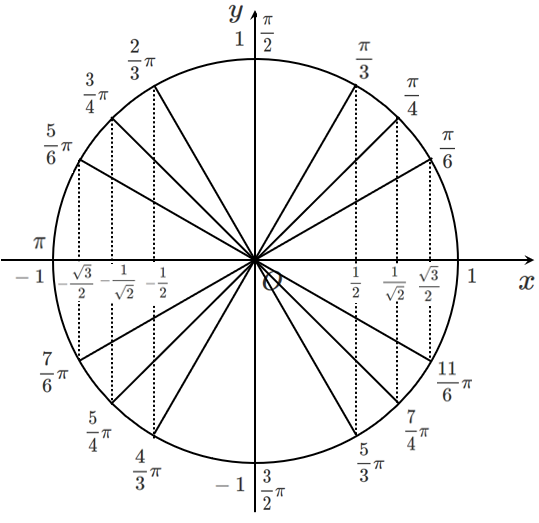

$\sin\theta$ も $\cos\theta$ も $\displaystyle{±\frac{1}{2},±\frac{1}{\sqrt{2}},±\frac{\sqrt{3}}{2}}$ のところに線を引くことになるね!

$\displaystyle{\frac{1}{2}<\frac{1}{\sqrt{2}}<\frac{\sqrt{3}}{2}}$ という大小関係を意識して線を引けば,角度は求まる!
$\tan$

「$\tan$ は傾き」を用いて方程式を解こう!
傾きが $1$ すなわち $x=1$ 上の点 $(1,1)$ を通る直線を引くと
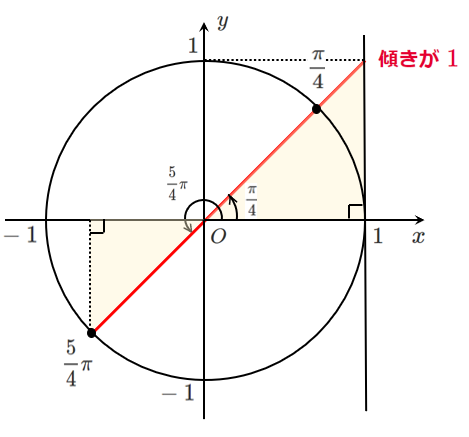
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{4},\frac{5}{4}\pi}$

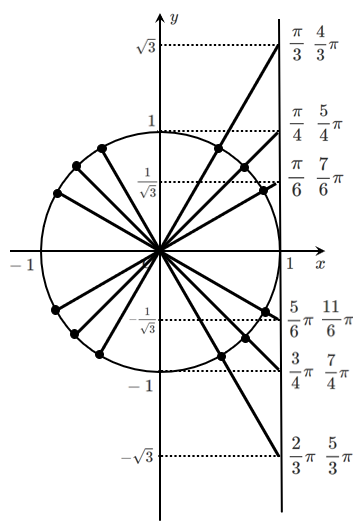
$\tan\theta$ の値についてまとめると以下のようになる!
問題
$0≦\theta<2\pi$ のとき,次の方程式を解け。
(1) $\displaystyle{\sin\theta=\frac{1}{\sqrt{2}}}$ (2) $\displaystyle{\sin\theta=-\frac{\sqrt{3}}{2}}$
(3) $\displaystyle{\cos\theta=\frac{\sqrt{3}}{2}}$ (4) $\displaystyle{\cos\theta=-\frac{1}{\sqrt{2}}}$
(5) $\displaystyle{\tan\theta=\frac{1}{\sqrt{3}}}$ (6) $\displaystyle{\tan\theta=-\sqrt{3}}$
(1) $\displaystyle{\sin\theta=\frac{1}{\sqrt{2}}}$
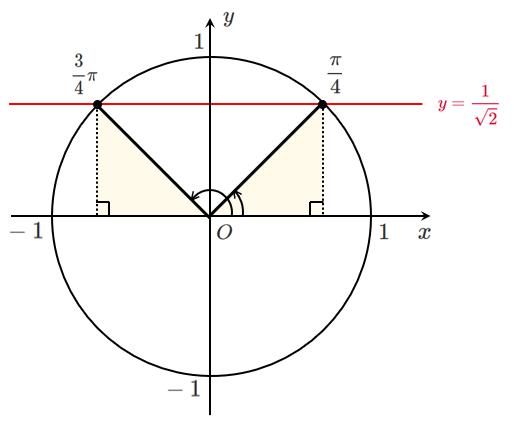
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{4},\frac{3}{4}\pi}$
(2) $\displaystyle{\sin\theta=-\frac{\sqrt{3}}{2}}$
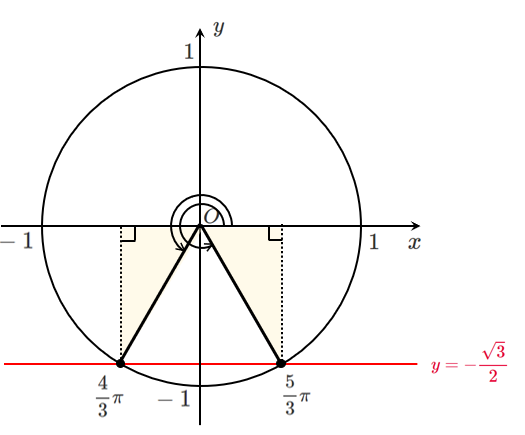
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{4}{3}\pi,\frac{5}{3}\pi}$
(3) $\displaystyle{\cos\theta=\frac{\sqrt{3}}{2}}$
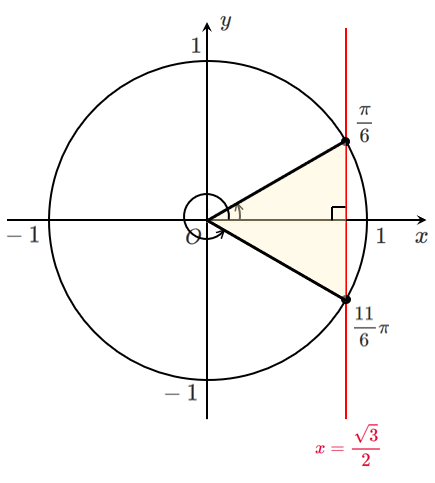
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{6},\frac{11}{6}\pi}$
(4) $\displaystyle{\cos\theta=-\frac{1}{\sqrt{2}}}$
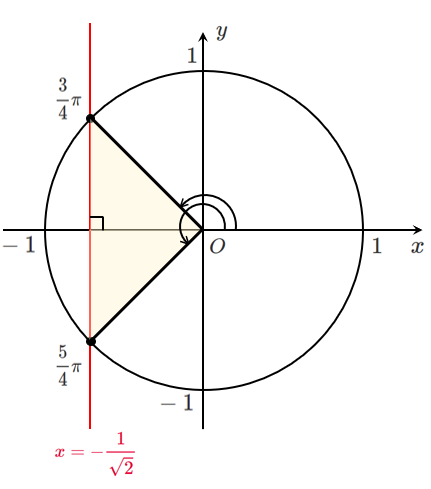
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{3}{4}\pi,\frac{5}{4}\pi}$
(5) $\displaystyle{\tan\theta=\frac{1}{\sqrt{3}}}$
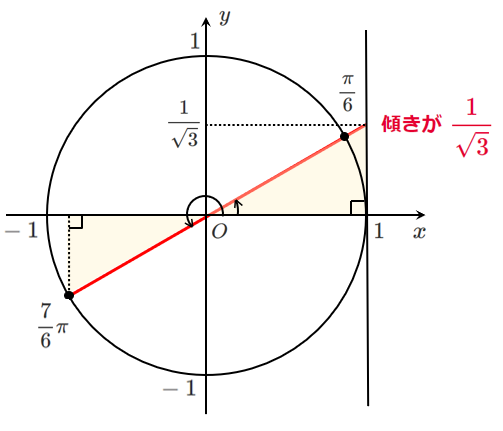
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{6},\frac{7}{6}\pi}$
(6) $\displaystyle{\tan\theta=-\sqrt{3}}$
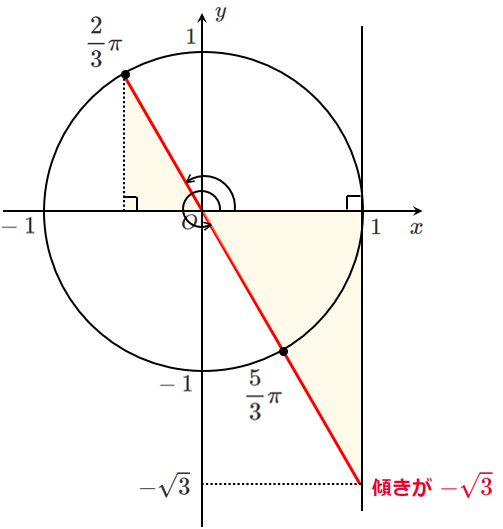
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{2}{3}\pi,\frac{5}{3}\pi}$
まとめ
● 三角関数を含む方程式のキーワード
$\sin$ は $y$ 座標
$\cos$ は $x$ 座標
$\tan$ は傾き

単位円をかいて確実に解けるようにしよう!




コメント