高校数学Ⅱで学ぶ『不等式の証明』の方法をわかりやすく解説!
証明と聞くと、反射的に苦手と感じる人も多いはず!
しかし、証明方法を理解して解くことで必ず解けるようになります!
この投稿を見れば、様々な不等式の証明パターンを網羅できます!
不等式の証明方法
(左辺)$>$(右辺) の証明は (左辺)ー(右辺)$>0$ を証明する
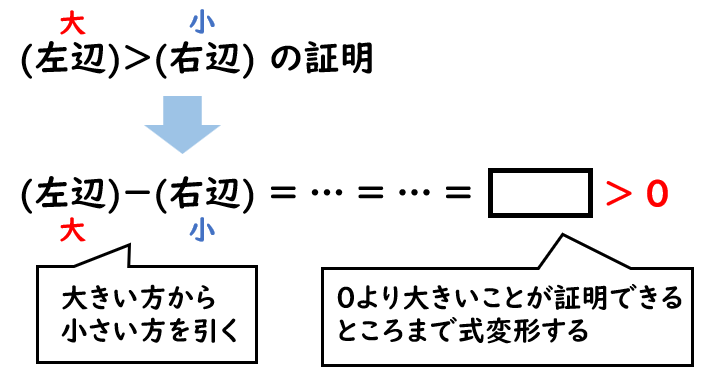
【補足】 (左辺)$<$(右辺) の証明は (右辺)-(左辺)$>0$ を証明する
「≧」や「≦」についても同様

不等式の証明は、まずは「差の形」を作ることがポイント!
条件付きの不等式の証明
(1) $x>y$ のとき、$2x+y>x+2y$
(2) $x>1$,$y>1$ のとき、$xy+1>x+y$
(1) $x>y$ すなわち $x-y>0$ を利用する
(2) $x>1$,$y>1$ すなわち $x-1>0$,$y-1>0$ を利用する
(左辺)-(右辺) を計算すると
$(2x+y)-(x+2y)=x-y$
$x>y$ より,$x-y>0$ であるから $(2x+y)-(x+2y)>0$
したがって $2x+y>x+2y$
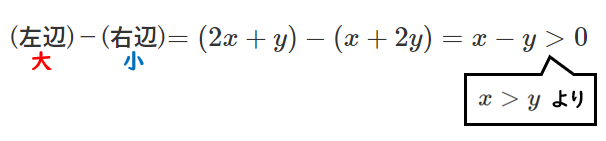
(2) $x>1$,$y>1$ のとき、$xy+1>x+y$
(左辺)-(右辺) を計算すると
$(xy+1)-(x+y)$
$=xy-x-y+1$
$=x(y-1)-(y-1)$
$=(x-1)(y-1)$
$x>1$,$y>1$ より,$x-1>0$,$y-1>0$ であるから
$(x-1)(y-1)>0$
よって $(xy+1)-(x+y)>0$
したがって $xy+1>x+y$
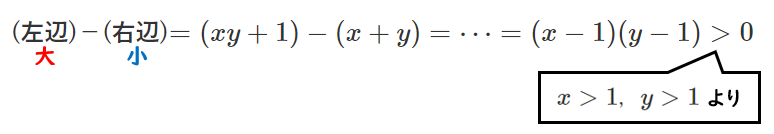
平方の性質を利用する不等式の証明
不等式 $A≧B$ の証明は、「等号が成り立つとき」を求めさせる問題が多いです。
不等式 $A≧B$ の「等号が成り立つとき」というのは、「$A=B$ が成り立つとき」という意味です。
不等式 $A≧B$ の証明は $A-B≧0$ を証明するので、等号が成り立つときは $A-B=0$ が成り立つときを考えればよいです。
つまり、$A-B$ を式変形した最後の式が $0$ になるときを考えるということです。
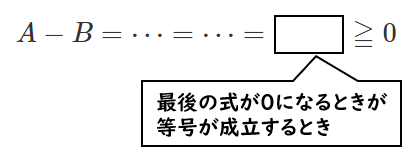
不等式の等号成立条件は、式変形の最後の式で考える
$\cdots=($$ $$)^2≧0$ ➡ 等号成立は $=0$ のとき
$\cdots=($$ $$)^2+($$ $$)^2≧0$ ➡ 等号成立は $=0$ かつ $=0$ のとき
(1) $x^2+2x+y^2-4y+5≧0$
(2) $x^2+5y^2≧4xy$
(1) $x^2+2x+y^2-4y+5≧0$
左辺を計算すると
$x^2+2x+y^2-4y+5$
$=(x+1)^2-1^2+(y-2)^2-2^2+5$
$=(x+1)^2+(y-2)^2≧0$
したがって $x^2+2x+y^2-4y+5≧0$
等号が成り立つのは,$x+1=0$ かつ $y-2=0$
すなわち $x=-1$,$y=2$ のときである

(2) $x^2+5y^2≧4xy$
(左辺)-(右辺) を計算すると
$(x^2+5y^2)-4xy$
$=x^2-4xy+5y^2$
$=(x-2y)^2-(2y)^2+5y^2$
$=(x-2y)^2+y^2≧0$
したがって $x^2+5y^2≧4xy$
等号が成り立つのは,$x-2y=0$ かつ $y=0$
すなわち $x=y=0$ のときである

平方の大小関係を利用する不等式の証明
不等式の証明では差をとる($A≧B$ $\Longleftrightarrow$ $A-B≧0$)ことが基本でした。
しかし、√(ルート)や絶対値を含む場合、このままでは差をとりにくいので、次のような不等式を考えます。
$A≧0$,$B≧0$ のとき, $A≧B$ $\Longleftrightarrow$ $A^2≧B^2$ $\Longleftrightarrow$ $A^2-B^2≧0$
つまり、「$0$ 以上の $A$ と $B$ は $2$ 乗しても大小関係は変わらないので、$2$ 乗して差をとって証明しよう」ということです。
ルートは $2$ 乗するとはずれる。 $(\sqrt{a})^2=a$
絶対値は $2$ 乗するとはずれる。 $|a|^2=a^2$
ルートと絶対値は $2$ 乗すると計算がしやすくなります。
これをまとめると次のようになります。
$A≧0$,$B≧0$ のとき, $A≧B$ の証明 ➡ $A^2-B^2≧0$ を証明せよ
ルートや絶対値を含む不等式の証明は、2乗して差をとる
(1) $x>0$,$y>0$ のとき,$\sqrt{x}+\sqrt{y}>\sqrt{x+y}$
(2) $|x|+|y|≧|x+y|$
(1) $x>0$,$y>0$ のとき,$\sqrt{x}+\sqrt{y}>\sqrt{x+y}$
両辺の平方($2$ 乗)の差を考えると
$(\sqrt{x}+\sqrt{y})^2-(\sqrt{x+y})^2$
$=(x+2\sqrt{xy}+y)-(x+y)$
$=2\sqrt{xy}>0$
よって $(\sqrt{x}+\sqrt{y})^2>(\sqrt{x+y})^2$
$\sqrt{x}+\sqrt{y}>0$,$\sqrt{x+y}>0$ より $\sqrt{x}+\sqrt{y}>\sqrt{x+y}$
(2) $|x|+|y|≧|x+y|$
両辺の平方($2$ 乗)の差を考えると
$(|x|+|y|)^2-|x+y|^2$
$=|x|^2+2|xy|+|y|^2-(x+y)^2$ ← $|x+y|^2=(x+y)^2$
$=x^2+2|xy|+y^2-(x^2+2xy+y^2)$ ←$|x|^2=x^2$,$|y|^2=y^2$
$=2(|xy|-xy)≧0$ ← $|xy|≧xy$
よって $(|x|+|y|)^2≧|x+y|^2$
$|x|+|y|≧0$,$|x+y|≧0$ より $|x|+|y|≧|x+y|$
等号が成り立つのは
$|ab|=ab$ すなわち $ab≧0$ のときである ← $|A|=A$ のとき $A≧0$
【補足】$|xy|≧xy$ の理由
正の数は絶対値をとっても同じ($|3|=3$)
負の数なら絶対値をとる方が大きい($|-3|>3$)
【注意】
不等式を平方の差をとって示すときは、「両辺がともに $0$ 以上である」ことがポイントです。
以下のように、負の場合だと大小関係が変わる場合があるからです。
$2$$>$$-3$ の両辺を $2$ 乗すると $4$$<$$9$




コメント