
不等式を座標平面に図示してみよう!
図形と方程式

座標平面上の図形と方程式の関係をみてみよう!
方程式 … 文字が含まれる等式
例えば,$y=x$,$y=x^2$ など
方程式を満たす $x$ と $y$ の組合せを座標平面上にとると図形ができる
$y=x$ を満たすような $x$ と $y$ の組合せを座標で表すと
$(0,0)$,$(1,1)$,$(2,2)$,$(-1,-1)$,$\cdots$
$x$ 座標と $y$ 座標が等しいような点が $y=x$ を満たすような点である
これらを図示すると,座標平面上に直線ができる
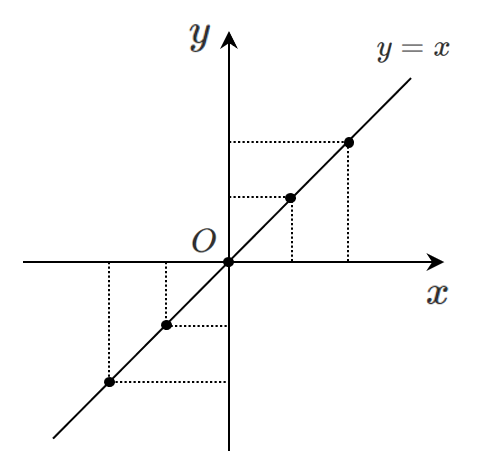
以上より,方程式 $y=x$ は座標平面上では直線を表す
不等式を満たす領域(直線)

不等式を満たす $x$,$y$ の組合せを座標平面上にとってみよう!
不等式 $y<x+1$ について
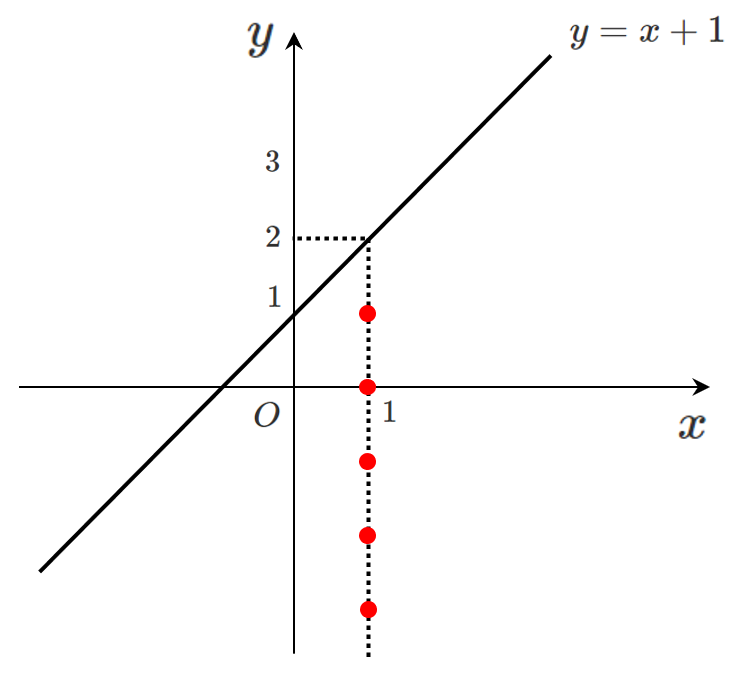
$x=1$ のとき $y<2$
すなわち $x$ 座標を $1$ で固定すると
不等式 $y<x+1$ を満たす点は
$(1,1)$,$(1,0)$,$(1,-1)$,$(1,-2)$,…
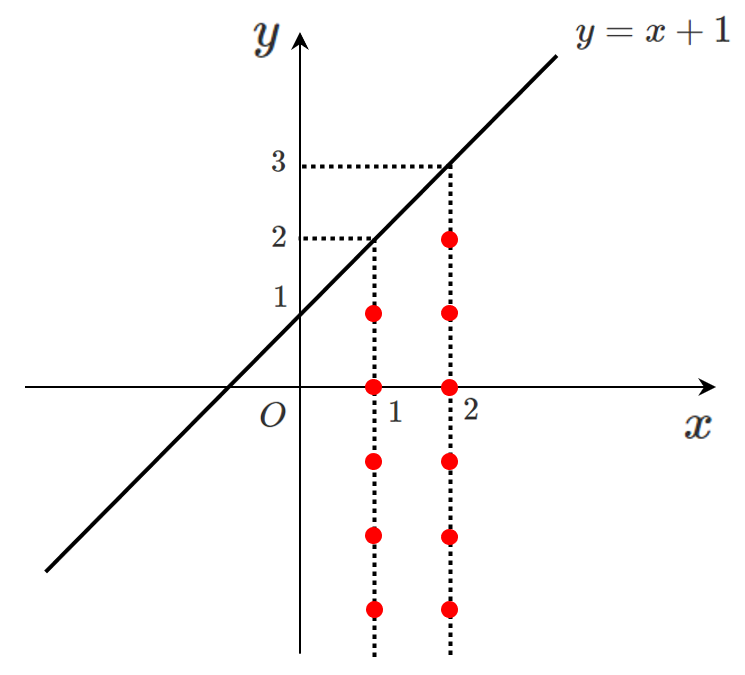
$x=2$ のとき $y<3$
すなわち $x$ 座標を $2$ で固定すると
不等式 $y<x+1$ を満たす点は
$(2,2)$,$(2,1)$,$(2,0)$,$(2,-1)$,…
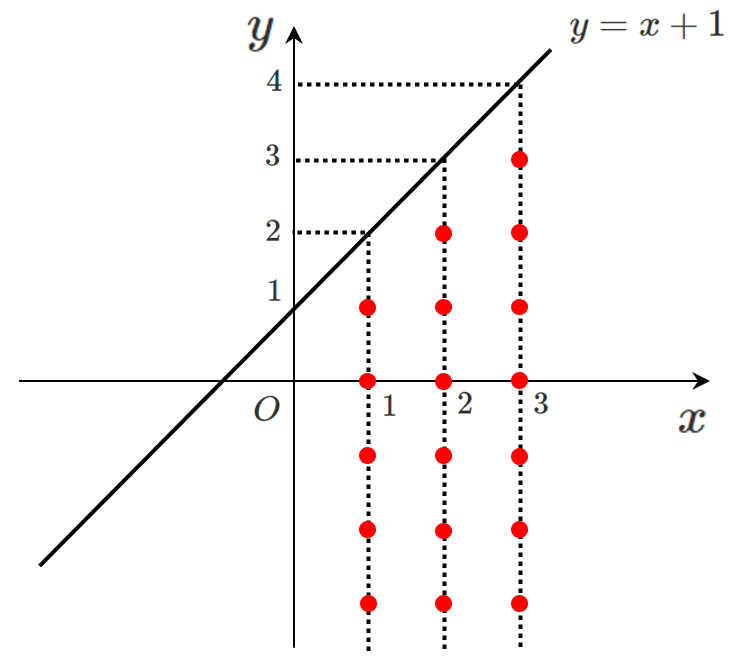
$x=3$ のとき $y<4$
すなわち $x$ 座標を $3$ で固定すると
不等式 $y<x+1$ を満たす点は
$(3,3)$,$(3,2)$,$(3,1)$,$(3,0)$,…
同様に,$x=0,-1,-2$ を考えると
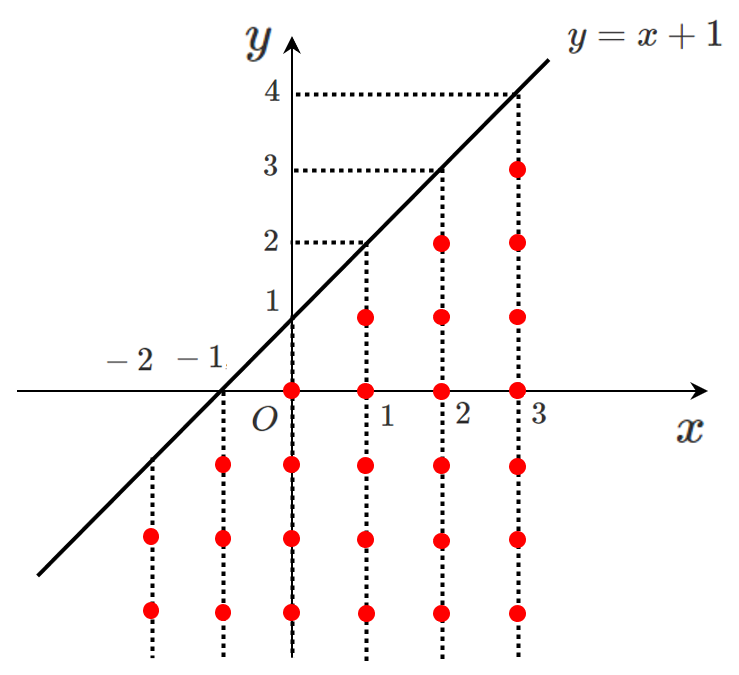
不等式 $y<x+1$ を満たす点は
直線 $y=x+1$ より下側の部分にある
これを不等式の満たす 領域 という
したがって,不等式 $y<x+1$ の領域を図示すると
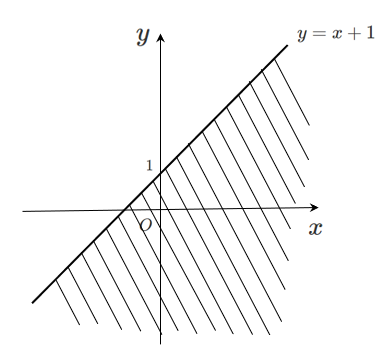
ただし,境界線($y=x+1$)は含まない
逆に,不等式 $y>x+1$ を考えると
不等式 $y>x+1$ を満たす点は
直線 $y=x+1$ より上側の部分にある
したがって,不等式 $y>x+1$ の領域を図示すると
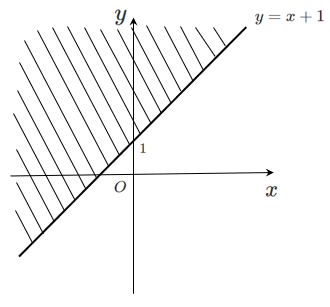
ただし,境界線($y=x+1$)は含まない

以上より,次のようにまとめることができる!
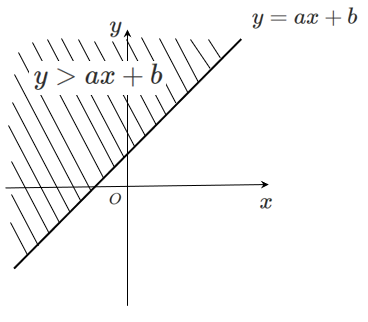
不等式 $y > ax+b$ は直線 $y=ax+b$ の上側の領域
ただし,境界線は含まない
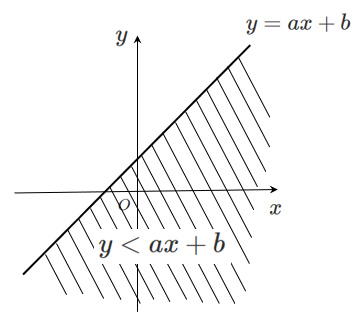
補足
不等式 $y ≦ ax+b$ は直線 $y=ax+b$ の下側の領域
不等式 $y ≧ ax+b$ は直線 $y=ax+b$ の上側の領域
ただし,境界線は含む
不等式 $x > 1$ を満たす点は
$x$ 座標が $1$ より大きいので
直線 $x=1$ より右側である
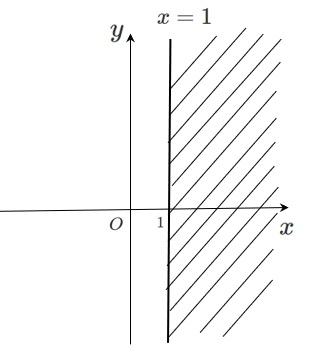
ただし,境界線は含まない
問題
(1) $x-y-1 > 0$
(2) $3x+2y+4≧0$
(3) $x+1≦0$
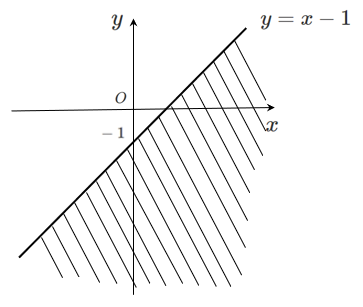
(1) $x-y-1>0$
式変形すると $y<x-1$
求める領域は,直線 $y=x-1$ の下側
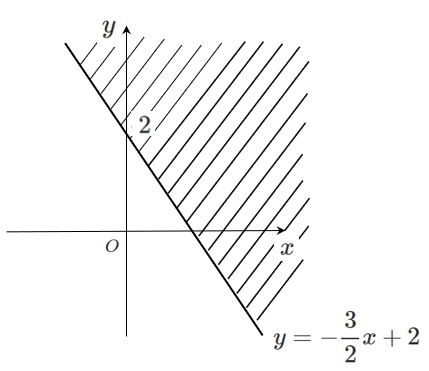
(2) $3x+2y-4≧0$
式変形すると $\displaystyle{y≧-\frac{3}{2}x+2}$
求める領域は,直線 $\displaystyle{y=-\frac{3}{2}x+2}$ の上側
(3) 不等式 $x+1≦0$
式変形すると $x≦-1$
求める領域は,直線 $x=-1$ の左側
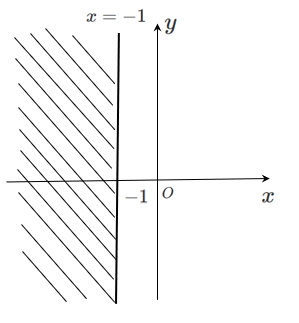

簡単に考えると,直線を書いてどちらかの領域に斜線を引くだけ!
不等式を満たす領域(円)
直線と同様に考えると,
境界線は $x^2+y^2=9$
すなわち 原点を中心とする半径 $3$ の円

不等式 $x^2+y^2<9$ を満たすような点は
$(0,0)$,$(1,0)$,$(0,1)$,$(1,1)$,
$(2,0)$,$(2,1)$,$(1,2)$,$(2,2)$,$\cdots$
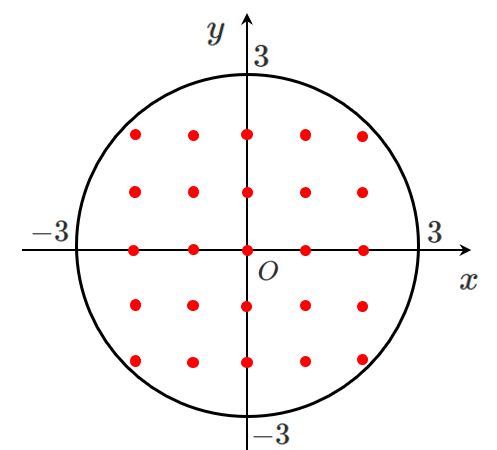
不等式 $x^2+y^2<9$ を満たす点は
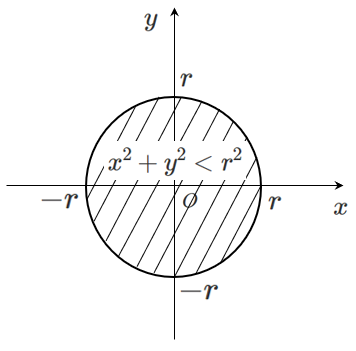
円 $x^2+y^2<9$ の内側の部分にある
したがって,不等式 $x^2+y^2<9$ の領域を図示すると
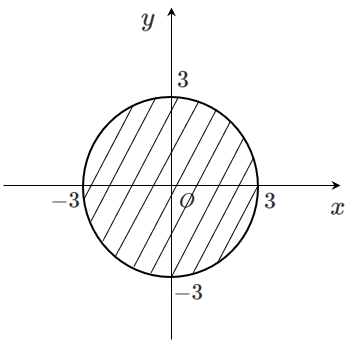
ただし,境界線($x^2+y^2=9$)は含まない
逆に,不等式 $x^2+y^2>9$ を考えると
不等式 $x^2+y^2>9$ を満たす点は
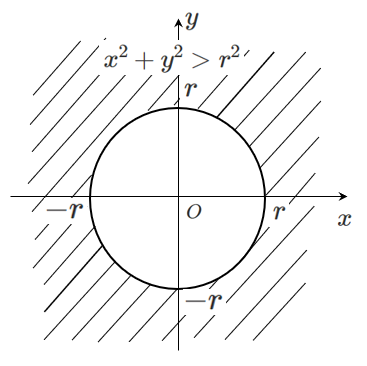
円 $x^2+y^2=9$ の外側の部分にある
したがって,不等式 $x^2+y^2>9$ の領域を図示すると
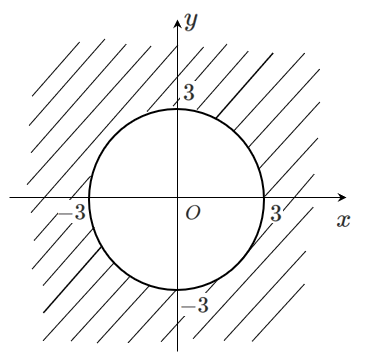
ただし,境界線は含まない

以上より,次のようにまとめることができる!
不等式 $x^2+y^2 > r^2$ は円 $x^2+y^2=r^2$ の外側の領域
ただし,境界線は含まない
補足
不等式 $x^2+y^2 ≦ r^2$ は円 $x^2+y^2=r^2$ の内側の領域
不等式 $x^2+y^2 ≧ r^2$ は円 $x^2+y^2=r^2$ の外側の領域
ただし,境界線は含む
問題
(1) $(x-1)^2+y^2 ≦ 1$
(2) $(x+1)^2+(y-1)^2>1$
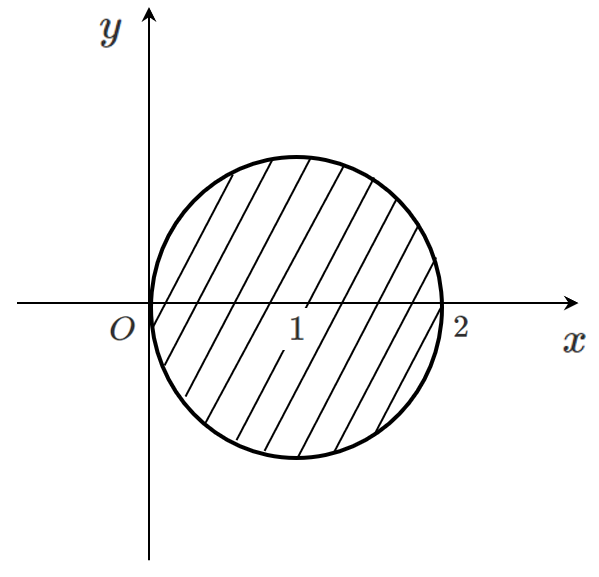
(1) $(x-1)^2+y^2 ≦ 1$
求める領域は,円 $(x-1)^2+y^2=1$ の内側
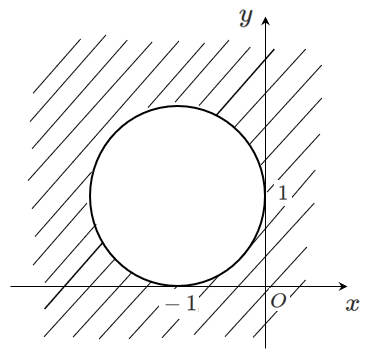
(2) $(x+1)^2+(y-1)^2>1$
求める領域は,円 $(x+1)^2+(y-1)^2=1$ の外側
もしも忘れた場合

直線の上側か下側かわからなくなったらどうしたらいい?

原点の座標を代入してみよう!
不等式 $y < x+1$ に $(0,0)$ を代入すると
$0 < 0+1$
となり,不等式が成り立つ
これより,原点は不等式を満たす領域に含まれていることがわかる
原点は直線 $y=x+1$ の下側の領域にあるので
不等式 $y < x+1$ は直線の下側である
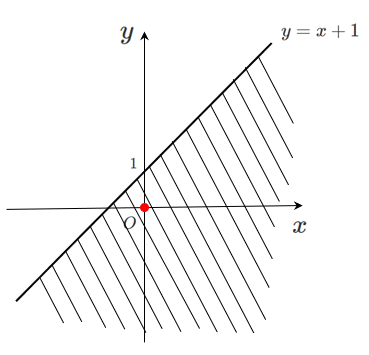

領域で困ったら,原点を代入!
不等式が成り立つなら,原点は求める領域に含まれる
不等式が成り立たないなら,原点は求める領域に含まれない
まとめ
● 不等式を満たす領域(直線)
不等式 $y < ax+b$ は直線 $y=ax+b$ の下側の領域
不等式 $y > ax+b$ は直線 $y=ax+b$ の上側の領域
ただし,境界線は含まない
● 不等式を満たす領域(円)
不等式 $x^2+y^2 < r^2$ は円 $x^2+y^2=r^2$ の内側の領域
不等式 $x^2+y^2 > r^2$ は円 $x^2+y^2=r^2$ の外側の領域
ただし,境界線は含まない

領域を図示できるようにしよう!




コメント