二重根号

高校数学Ⅰで習う『二重根号』は苦手な人が多いです！
しかし，理屈をきちんとおさえれば簡単に理解できます！
『二重根号』が苦手な人でもわかりやすく解説します！
この投稿を見れば，『二重根号』で迷うことはなくなります！

二重根号とは

『二重根号』とは　根号（$\sqrt{　}$）の中に，根号（$\sqrt{　}$）が入っている式　のことです。

　例　$\sqrt{5+2\sqrt{6}}$，$\sqrt{8-4\sqrt{3}}$

『二重根号』は　　$\sqrt{5+2\sqrt{6}}=\sqrt{3}+\sqrt{2}$

のように外すことができる場合があり，

『二重根号』に関する問題は「二重根号を外して簡単にする」というものになります。

後で出てきますが，二重根号を外せない場合もあるので注意が必要です。

二重根号を外すための公式

まずはこの公式から覚えよう！

両辺を $2$ 乗しても証明できるね！

二重根号を外す方法

基本編

　$a+b=4$，$ab=3$ となるような $a$，$b$（$a>0$，$b>0$)
　すなわち，和が $4$，積が $3$ である $2$ 数を求める

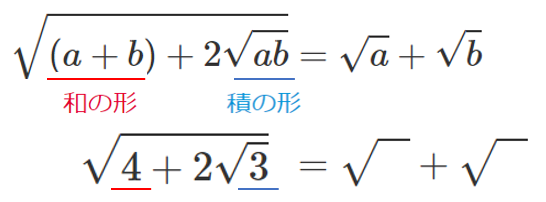
　積が $3$ になる $2$ 数を考えると，$a=3$，$b=1$ であることが分かる

$$\sqrt{4+2\sqrt{3}}=\sqrt{3}+\sqrt{1}=\sqrt{3}+1$$

応用編

$\sqrt{　}$ の前の数字が $4$ だから，公式が使えないね…

こういうときは，$2$ を強引に作りだそう！

$\sqrt{7-4\sqrt{3}} = \sqrt{\sqrt{7}-2\sqrt{12}}$

$$\sqrt{7-4\sqrt{3}} = \sqrt{7-2\sqrt{12}}$$

　$a+b=7$，$ab=12$ となるような $a$，$b$（$a>b>0$)
　すなわち，和が $7$，積が $12$ である $2$ 数を求める

　積が $12$ になる $2$ 数を考えると，$a=4$，$b=3$ であることが分かる

\begin{align} \sqrt{7-4\sqrt{3}} &= \sqrt{\sqrt{7}-2\sqrt{12}} \\ & = \sqrt{4}-\sqrt{3} \\ & = 2-\sqrt{3} \end{align}

$\sqrt{7-2\sqrt{12}}=\sqrt{3}-\sqrt{4}$ としないように！

左辺は正，右辺は負となって式が成り立たなくなるよ！

この場合は以下のような式変形で，$2$ を強引に出そう！

$\displaystyle{\sqrt{3+\sqrt{5}}=\sqrt{\frac{6+2\sqrt{5}}{2}}}$

二重根号が外れない場合と判定方法

二重根号が外せない場合があるの？

例えば，$\sqrt{5+2\sqrt{3}}$ を考えてみよう！

この場合，和が $5$，積が $3$ である $2$ 数を考えるけど，

そのような自然数の組は存在しない！

こんなときは二重根号を外すことができないよ！

簡単に見分ける方法はないの？

＜解説＞

　$\sqrt{A\pm2\sqrt{B}}$ について，和が $A$，積が $B$ である自然数の組 $a$，$b$ が存在する条件は

　$x^2-Ax+B=0$ の解が $2$ つとも自然数であること

　よって，判別式 $A^2-4B$ が平方数であることが必要

　逆に，判別式が平方数なら，解が $2$ つとも自然数である

このことを知っていると，二重根号を外せるかどうかが簡単に判定できるね！

🔰基本…まずはこの記事から！
🔵標準…基本問題や公式の理解度が重要！
🔴応用…場合分けなど思考力が要求される！