数学Ⅱで学ぶ『二項定理の一般項』を利用した問題をわかりやすく解説します!
「二項定理が苦手」という高校生が多いですが、
重要なのは二項定理の一般項の基本をおさえながら問題演習を積むことです!
二項定理が苦手な人はぜひ参考にしてください!
問題
(2) $\displaystyle{\left(2x-\frac{1}{x}\right)^6}$ における $x^2$ の係数を求めよ。
(3) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ における $\displaystyle{\frac{1}{x^3}}$ の係数を求めよ。
(4) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ における定数項を求めよ。
(1) $\displaystyle{\left(2x+\frac{1}{x}\right)^5}$ [$x$]
$\displaystyle{\left(2x+\frac{1}{x}\right)^5}$ の展開式における一般項は
\begin{eqnarray} & & _5 C _r (2x)^{5-r}\left(\frac{1}{x}\right)^r \\\\ & = & _5 C _r 2^{5-r}\frac{x^{5-r}}{x^r} \\\\ & = & _5 C _r 2^{5-r}x^{5-2r} (r=0,1,2,\cdots,5) \cdots ①\\\\ \end{eqnarray}$x^{5-2r}=x$ すなわち $5-2r=1$ を解いて $r=2$
①に $r=2$ を代入して $x$ の係数を求めると $_5C_2 2^3=80$
【別解】『5つの ( ) から $2x$ が3つ、$\displaystyle{\frac{1}{x}}$ が2つでてくると $x$ ができる』ので、
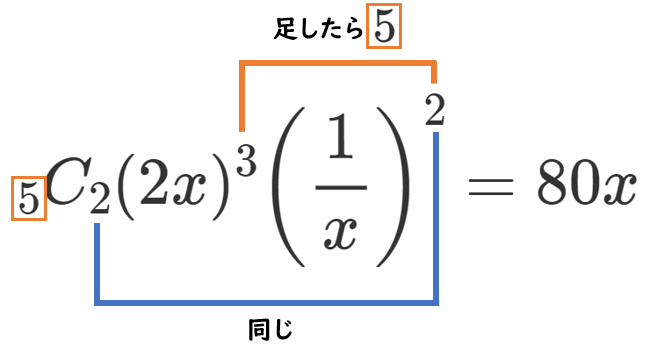
(2) $\displaystyle{\left(2x-\frac{1}{x}\right)^6}$ [$x^2$]
$\displaystyle{\left(2x-\frac{1}{x}\right)^6}$ の展開式における一般項は
\begin{eqnarray} & & _6 C _r (2x)^{6-r}\left(-\frac{1}{x}\right)^r \\\\ & = & _6 C _r 2^{6-r}(-1)^r\frac{x^{6-r}}{x^r} \\\\ & = & _6 C _r 2^{6-r}(-1)^rx^{6-2r} (r=0,1,2,\cdots,6) \cdots ①\\\\ \end{eqnarray}$x^{6-2r}=x^2$ すなわち $6-2r=2$ を解いて $r=2$
①に $r=2$ を代入して $x^2$ の係数を求めると $_6C_2 2^4(-1)^2=240$
【別解】『6つの ( ) から $2x$ が4つ、$\displaystyle{-\frac{1}{x}}$ が2つでてくると $x^2$ ができる』ので、
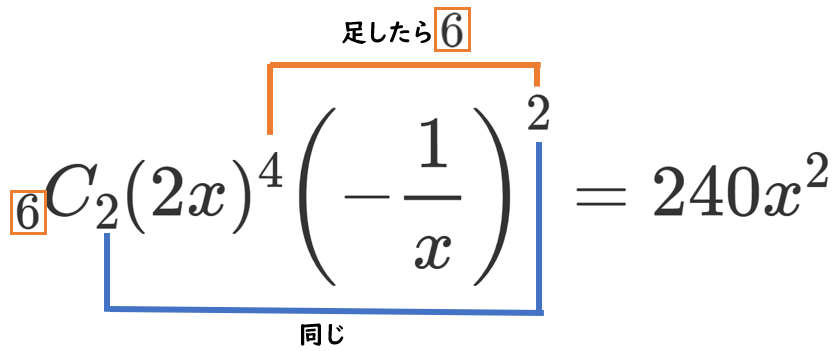
(3) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ $\displaystyle{\left[\frac{1}{x^3}\right]}$
$\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ の展開式における一般項は
\begin{eqnarray} & & _6 C _r (2x^2)^{6-r}\left(-\frac{1}{x}\right)^r \\\\ & = & _6 C _r 2^{6-r}(-1)^r\frac{x^{12-2r}}{x^r} \\\\ & = & _6 C _r 2^{6-r}(-1)^rx^{12-3r} (r=0,1,2,\cdots,6) \cdots ①\\\\ \end{eqnarray}$\displaystyle{x^{12-3r}=\frac{1}{x^3}}$ すなわち $12-3r=-3$ を解いて $r=5$
①に $r=5$ を代入して $\displaystyle{\frac{1}{x^3}}$ の係数を求めると $_6C_5 2^1(-1)^5=-12$
【別解】『6つの ( ) から $2x^2$ が1つ、$\displaystyle{-\frac{1}{x}}$ が5つでてくると $\displaystyle{\frac{1}{x^3}}$ ができる』ので、
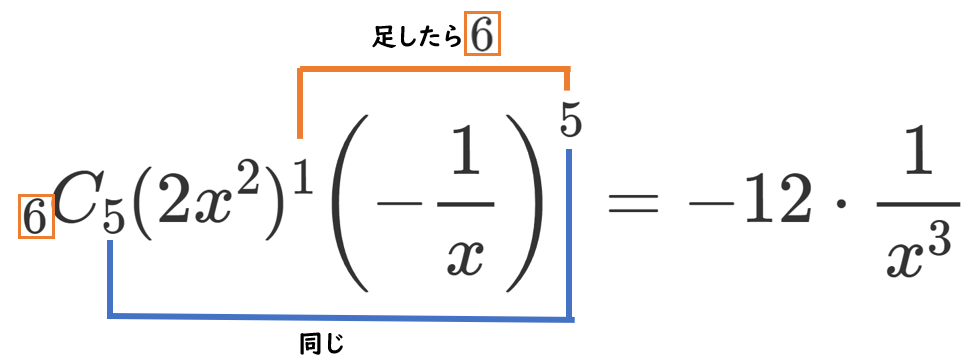
(4) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ [定数項]
$\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ の展開式における一般項は
\begin{eqnarray} & & _6 C _r (2x^2)^{6-r}\left(-\frac{1}{x}\right)^r \\\\ & = & _6 C _r 2^{6-r}(-1)^r\frac{x^{12-2r}}{x^r} \\\\ & = & _6 C _r 2^{6-r}(-1)^rx^{12-3r} (r=0,1,2,\cdots,6) \cdots ①\\\\ \end{eqnarray}$\displaystyle{x^{12-3r}=x^0}$ すなわち $12-3r=0$ を解いて $r=4$
①に $r=4$ を代入して $\displaystyle{\frac{1}{x^3}}$ の係数を求めると $_6C_4 2^2(-1)^4=60$
【別解】『6つの ( ) から $2x^2$ が2つ、$\displaystyle{-\frac{1}{x}}$ が4つでてくると定数項ができる』ので、
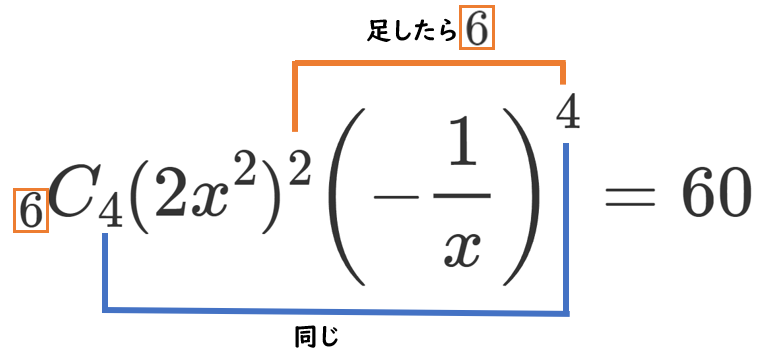
二項定理とは
$\Longleftrightarrow$ $\displaystyle{(a+b)^n=\sum_{r=0}^n {_n C_r a^{n-r}b^r}}$
『二項定理』とは、2項の累乗の式 $(a+b)^n$ の展開の公式のことです。
『二項定理』を用いることで、2項の累乗の式、例えば (a+b)^5$ という式の展開ができたり、各項の係数を求めたりすることができます。
↓↓二項定理の原理を学びたい人はこちら↓↓

例として、$(a+b)^2$ の展開を考えてみます。
$(a+b)^2=a^2+2ab+b^2$ は覚えていると思いますが、$(a+b)^2$ の展開は $(a+b)(a+b)$ と考えて分配法則を使うことで展開できます。
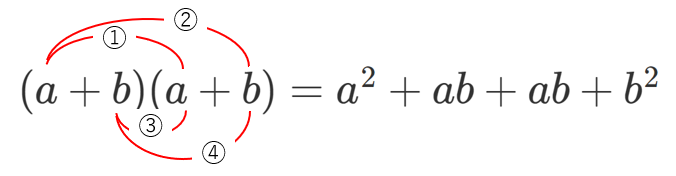
分配法則をもう少し丁寧に見てみると、『それぞれの ( ) から1つずつ取り出してかける』という計算を行っています。
①1つ目の ( ) から $a$、2つ目の ( ) から $a$ をかけると $a^2$
②1つ目の ( ) から $a$、2つ目の ( ) から $b$ をかけると $ab$
③1つ目の ( ) から $b$、2つ目の ( ) から $a$ をかけると $ab$
④1つ目の ( ) から $b$、2つ目の ( ) から $b$ をかけると $b^2$
もちろん、$ab$ が同類項としてまとめることができるので $2ab$ となります。
$ab$ が2つ出てくる理由は、
『2つの ( ) から $a$ が1つ、$b$ が1つ出てくるのが2通りあるから』です。
つまり、
『2つの ( ) から $b$ がでてくる ( ) を1つ選ぶ』
※ $a$ がでてくる ( ) を選ぶでもよい
と考えることができるので $ab$ の係数である $2$ は $_2 C_1$ と表すことができます
数学Ⅱで習う $(a+b)^3$ に二項定理を用いると
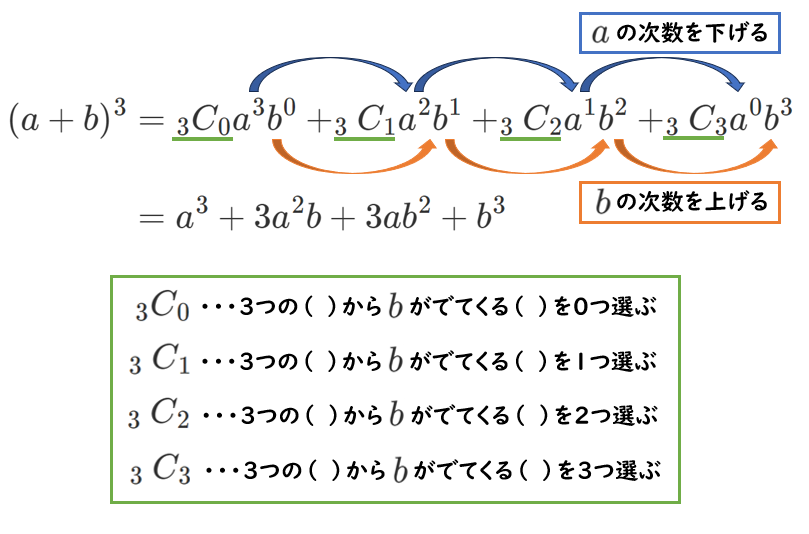
二項定理の一般項とは
$(a+b)^n$ の展開式について、
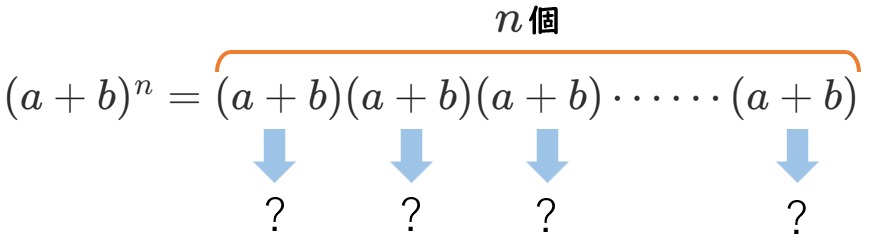
$a^{n-3}b^3$ の係数は『$n$ 個の ( ) から $b$ がでてくる ( ) を $3$ 個選ぶ』ので、$_n C_3$
同様に、
$a^{n-r}b^r$ の係数は『$n$ 個の ( ) から $b$ がでてくる ( ) を $r$ 個選ぶ』ので、$_n C_r$ となる。
このとき、$_n C_r a^{n-r}b^r$ を一般項といいます。
一般項を用いて、二項定理の問題を解いていくことになります。

文字がいっぱいでわかりにくい人はこれを参考に!

問題解説
(2) $\displaystyle{\left(2x-\frac{1}{x}\right)^6}$ における $x^2$ の係数を求めよ。
(3) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ における $\displaystyle{\frac{1}{x^3}}$ の係数を求めよ。
(4) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ における定数項を求めよ。
<解答の手順>
1. 一般項を式変形をしていく
※指数法則に注意
$(x^2)^{6-2r}=x^{2(6-2r)}$ $\displaystyle{\frac{x^{5-r}}{x^r}=x^{5-r-r}}$ など
2. $r$ の値を計算して一般項に代入する
【別解のように $r$ の値を予想して解くこともできる】
(1) $\displaystyle{\left(2x+\frac{1}{x}\right)^5}$ [$x$]
$\displaystyle{\left(2x+\frac{1}{x}\right)^5}$ の展開式における一般項は
\begin{eqnarray} & & _5 C _r (2x)^{5-r}\left(\frac{1}{x}\right)^r \\\\ & = & _5 C _r 2^{5-r}\frac{x^{5-r}}{x^r} \\\\ & = & _5 C _r 2^{5-r}x^{5-2r} (r=0,1,2,\cdots,5) \cdots ①\\\\ \end{eqnarray}$x^{5-2r}=x$ すなわち $5-2r=1$ を解いて $r=2$
①に $r=2$ を代入して $x$ の係数を求めると $_5C_2 2^3=80$
【別解】『5つの ( ) から $2x$ が3つ、$\displaystyle{\frac{1}{x}}$ が2つでてくると $x$ ができる』ので、

(2) $\displaystyle{\left(2x-\frac{1}{x}\right)^6}$ [$x^2$]
$\displaystyle{\left(2x-\frac{1}{x}\right)^6}$ の展開式における一般項は
\begin{eqnarray} & & _6 C _r (2x)^{6-r}\left(-\frac{1}{x}\right)^r \\\\ & = & _6 C _r 2^{6-r}(-1)^r\frac{x^{6-r}}{x^r} \\\\ & = & _6 C _r 2^{6-r}(-1)^rx^{6-2r} (r=0,1,2,\cdots,6) \cdots ①\\\\ \end{eqnarray}$x^{6-2r}=x^2$ すなわち $6-2r=2$ を解いて $r=2$
①に $r=2$ を代入して $x^2$ の係数を求めると $_6C_2 2^4(-1)^2=240$
【別解】『6つの ( ) から $2x$ が4つ、$\displaystyle{-\frac{1}{x}}$ が2つでてくると $x^2$ ができる』ので、

(3) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ $\displaystyle{\left[\frac{1}{x^3}\right]}$
$\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ の展開式における一般項は
\begin{eqnarray} & & _6 C _r (2x^2)^{6-r}\left(-\frac{1}{x}\right)^r \\\\ & = & _6 C _r 2^{6-r}(-1)^r\frac{x^{12-2r}}{x^r} \\\\ & = & _6 C _r 2^{6-r}(-1)^rx^{12-3r} (r=0,1,2,\cdots,6) \cdots ①\\\\ \end{eqnarray}$\displaystyle{x^{12-3r}=\frac{1}{x^3}}$ すなわち $12-3r=-3$ を解いて $r=5$
①に $r=5$ を代入して $\displaystyle{\frac{1}{x^3}}$ の係数を求めると $_6C_5 2^1(-1)^5=-12$
【別解】『6つの ( ) から $2x^2$ が1つ、$\displaystyle{-\frac{1}{x}}$ が5つでてくると $\displaystyle{\frac{1}{x^3}}$ ができる』ので、

(4) $\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ [定数項]
$\displaystyle{\left(2x^2-\frac{1}{x}\right)^6}$ の展開式における一般項は
\begin{eqnarray} & & _6 C _r (2x^2)^{6-r}\left(-\frac{1}{x}\right)^r \\\\ & = & _6 C _r 2^{6-r}(-1)^r\frac{x^{12-2r}}{x^r} \\\\ & = & _6 C _r 2^{6-r}(-1)^rx^{12-3r} (r=0,1,2,\cdots,6) \cdots ①\\\\ \end{eqnarray}$\displaystyle{x^{12-3r}=x^0}$ すなわち $12-3r=0$ を解いて $r=4$
①に $r=4$ を代入して $\displaystyle{\frac{1}{x^3}}$ の係数を求めると $_6C_4 2^2(-1)^4=60$
【別解】『6つの ( ) から $2x^2$ が2つ、$\displaystyle{-\frac{1}{x}}$ が4つでてくると定数項ができる』ので、





コメント