数学Ⅱで学ぶ『二項定理』の基本をわかりやすく解説します!
「二項定理は式が長くてわからない」
「Cが急に出てきて意味不明」
という高校生が多いです!
式の展開の仕組みを理解することで、二項定理の理解が深まり、問題を解くのが非常に楽になります!
この投稿では、二項定理の原理とその使い方を例を交えながら、わかりやすく解説します!
二項定理が苦手な人はぜひ参考にしてください!

今回の問題はこれ↓
(2) $(x+3)^6$ における $x^4$ の係数を求めよ。
(3) $(x-2)^5$ における $x^2$ の係数を求めよ。
(4) $(3x+2y)^6$ における $x^4y^2$ の係数を求めよ。
(1) $(a+b)^5$ [$a^3b^2$]
$(a+b)^5$ の一般項は $_5C _r a^{5-r}b^r$
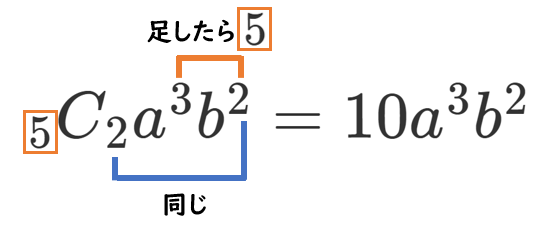
$a^3b^2$ の項は $r=2$ のときなので $_5 C _2 a^3b^2=10a^3b^2$
よって、求める係数は $10$
【別解】『5つの ( ) から $b$ がでてくる ( ) を2つ選ぶ』ので、
(2) $(x+3)^6$ [$x^4$]
$(x+3)^6$ の一般項は $_6C _r x^{6-r}\cdot3^r$
$x^4$ の項は $r=2$ のときなので $_6 C _2 x^4\cdot3^2=135x^4$
よって、求める係数は $135$
【別解】『6つの ( ) から $x$ がでてくる ( ) を4つ選ぶ』
すなわち『6つの ( ) から $3$ がでてくる ( ) を2つ選ぶ』ので、

(3) $(x-2)^5$ [$x^2$]
$(x-2)^5$ の一般項は $_5C _r x^{5-r}(-2)^r$
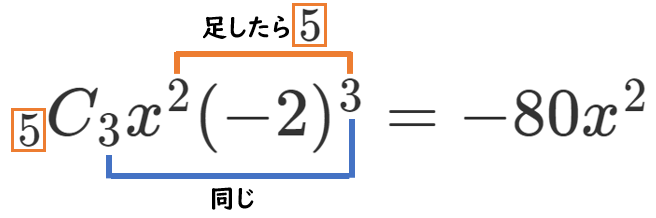
$x^2$ の項は $r=3$ のときなので $_5 C _3 x^2(-2)^3=-80x^2$
よって、求める係数は $-80$
【別解】『5つの ( ) から $x$ がでてくる ( ) を2つ選ぶ』
すなわち『5つの ( ) から $-2$ がでてくる ( ) を3つ選ぶ』ので、
(4) $(3x+2y)^6$ [$x^4y^2$]
$(3x+2y)^6$ の一般項は $_6C _r (3x)^{6-r}(2y)^r$
$x^4y^2$ の項は $r=2$ のときなので $_6 C _2 (3x)^4(2y)^2=4860x^4y^2$
よって、求める係数は $4860$
【別解】『6つの ( ) から $3x$ がでてくる ( ) を4つ選ぶ』
すなわち『6つの ( ) から $2y$ がでてくる ( ) を2つ選ぶ』ので、

二項定理とは
$\Longleftrightarrow$ $\displaystyle{(a+b)^n=\sum_{r=0}^n {_n C_r a^{n-r}b^r}}$
『二項定理』とは、2項の累乗の式 $(a+b)^n$ の展開の公式のことです。
『二項定理』を用いることで、2項の累乗の式、例えば $(a+b)^5$ という式の展開ができたり、各項の係数を求めたりすることができます。
なぜCが出てくるか
『二項定理』の最大の謎といってもよい「展開の公式になぜCが出てくるのか」について説明したいと思います。

展開した式にCがでてくる理由がわからない!

具体例を参考にして考えてみよう!
(a+b)² を例に
まずは例として、$(a+b)^2$ の展開を考えてみます。
$(a+b)^2=a^2+2ab+b^2$ は覚えていると思いますが、$(a+b)^2$ の展開は $(a+b)(a+b)$ と考えて分配法則を使うことで展開できます。
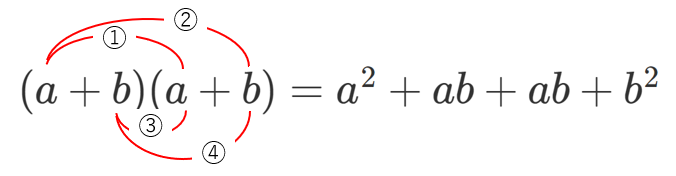
分配法則をもう少し丁寧に見てみると、『それぞれの ( ) から1つずつ取り出してかける』という計算を行っています。
①1つ目の ( ) から $a$、2つ目の ( ) から $a$ をかけると $a^2$
②1つ目の ( ) から $a$、2つ目の ( ) から $b$ をかけると $ab$
③1つ目の ( ) から $b$、2つ目の ( ) から $a$ をかけると $ab$
④1つ目の ( ) から $b$、2つ目の ( ) から $b$ をかけると $b^2$
もちろん、$ab$ が同類項としてまとめることができるので $2ab$ となります。
$ab$ が2つ出てくる理由は、
『2つの ( ) から $a$ が1つ、$b$ が1つ出てくるのが2通りあるから』です。
つまり、
『2つの ( ) から $b$ がでてくる ( ) を1つ選ぶ』
※ $a$ がでてくる ( ) を選ぶでもよい
と考えることができるので $ab$ の係数である $2$ は $_2 C_1$ と表すことができます。

『( ) からでてくるものを選ぶ』からCが使われるんだね!
(a+b)³ を例に
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$ についても、
以下のように $a^2b$ の係数である $3$ は $_3 C_1$ と考えることができます。
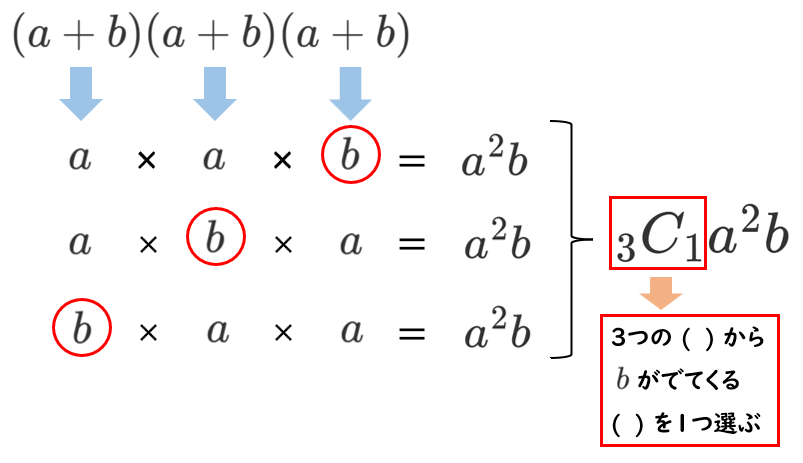
同様に、
$a^3$ の係数は『3つの ( ) から $b$ がでてくる ( ) を0つ選ぶ』ので、$_3 C_0$
$ab^2$ の係数は『3つの ( ) から $b$ がでてくる ( ) を2つ選ぶ』ので、$_3 C_2$
$b^3$ の係数は『3つの ( ) から $b$ がでてくる ( ) を3つ選ぶ』ので、$_3 C_3$
と考えることができます。
よって、
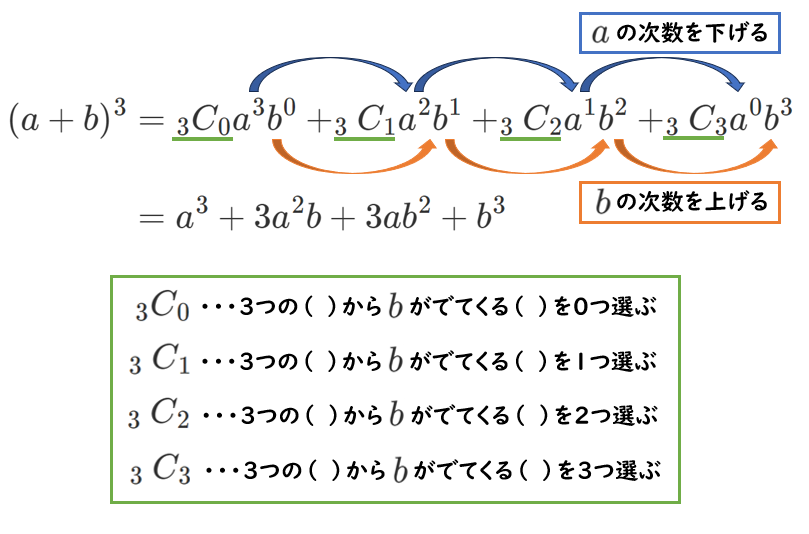

右にいくにつれて、
$a$ の次数を下げて $b$ の次数を上げる!
(a+b)⁴ を例に
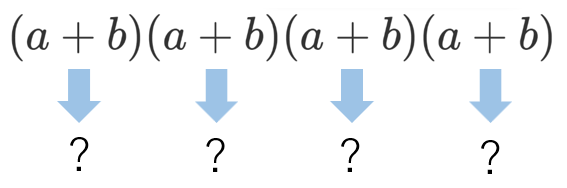
『4つの ( ) から $b$ がでてくる ( ) を0つ選ぶ』➡ $a^4b^0$ の係数は $_4 C_0$
『4つの ( ) から $b$ がでてくる ( ) を1つ選ぶ』➡ $a^3b^1$ の係数は $_4 C_1$
『4つの ( ) から $b$ がでてくる ( ) を2つ選ぶ』➡ $a^2b^2$ の係数は $_4 C_2$
『4つの ( ) から $b$ がでてくる ( ) を3つ選ぶ』➡ $a^1b^3$ の係数は $_4 C_3$
『4つの ( ) から $b$ がでてくる ( ) を4つ選ぶ』➡ $a^0b^4$ の係数は $_4 C_4$
一般項と二項係数
$(a+b)^n$ の展開式について、
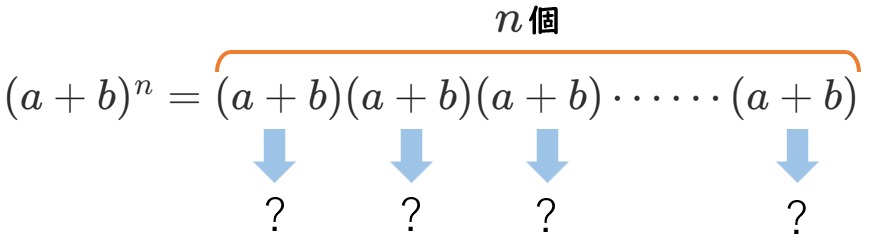
$a^{n-3}b^3$ の係数は『$n$ 個の ( ) から $b$ がでてくる ( ) を $3$ 個選ぶ』ので、$_n C_3$
同様に、
$a^{n-r}b^r$ の係数は『$n$ 個の ( ) から $b$ がでてくる ( ) を $r$ 個選ぶ』ので、$_n C_r$ となる。
このとき、$_n C_r a^{n-r}b^r$ を一般項、$_n C _r$ を二項係数といいます。
一般項を用いて、二項定理の問題を解いていくことになります。

文字がいっぱいでわかりにくい人はこれを参考に!

問題
(2) $(x+3)^6$ における $x^4$ の係数を求めよ。
(3) $(x-2)^5$ における $x^2$ の係数を求めよ。
(4) $(3x+2y)^6$ における $x^4y^2$ の係数を求めよ。
(1) $(a+b)^5$ [$a^3b^2$]
$(a+b)^5$ の一般項は $_5C _r a^{5-r}b^r$
$a^3b^2$ の項は $r=2$ のときなので $_5 C _2 a^3b^2=10a^3b^2$
よって、求める係数は $10$
【別解】『5つの ( ) から $b$ がでてくる ( ) を2つ選ぶ』ので、

(2) $(x+3)^6$ [$x^4$]
$(x+3)^6$ の一般項は $_6C _r x^{6-r}\cdot3^r$
$x^4$ の項は $r=2$ のときなので $_6 C _2 x^4\cdot3^2=135x^4$
よって、求める係数は $135$
【別解】『6つの ( ) から $x$ がでてくる ( ) を4つ選ぶ』
すなわち『6つの ( ) から $3$ がでてくる ( ) を2つ選ぶ』ので、

(3) $(x-2)^5$ [$x^2$]
$(x-2)^5$ の一般項は $_5C _r x^{5-r}(-2)^r$
$x^2$ の項は $r=3$ のときなので $_5 C _3 x^2(-2)^3=-80x^2$
よって、求める係数は $-80$
【別解】『5つの ( ) から $x$ がでてくる ( ) を2つ選ぶ』
すなわち『5つの ( ) から $-2$ がでてくる ( ) を3つ選ぶ』ので、

(4) $(3x+2y)^6$ [$x^4y^2$]
$(3x+2y)^6$ の一般項は $_6C _r (3x)^{6-r}(2y)^r$
$x^4y^2$ の項は $r=2$ のときなので $_6 C _2 (3x)^4(2y)^2=4860x^4y^2$
よって、求める係数は $4860$
【別解】『6つの ( ) から $3x$ がでてくる ( ) を4つ選ぶ』
すなわち『6つの ( ) から $2y$ がでてくる ( ) を2つ選ぶ』ので、

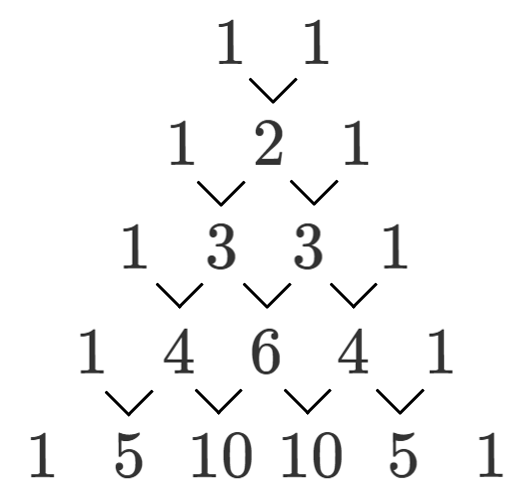
【補足】パスカルの三角形
$(a+b)^n$ の展開式の項の係数には規則性があります。
$(a+b)=$$1$$a+$$1$$b$
$(a+b)^2=$$1$$a^2+$$2$$ab+$$1$$b^2$
$(a+b)^3=$$1$$a^3+$$3$$a^2b+$$3$$ab^2+$$1$$b^3$
$(a+b)^4=$$1$$a^4+$$4$$a^3b+$$6$$a^2b^2+$$4$$ab^3+$$1$$b^4$
$(a+b)^5=$$1$$a^5+$$5$$a^4b+$$10$$a^3b^2+$$10$$a^2b^3+$$5$$ab^4+$$1$$b^5$
項の係数を並べてできるものを『パスカルの三角形』といいます。
<規則性>
- 各段の両端は $1$
- それ以外の数は、左上の数と右上の数の和




コメント