内分点と外分点におけるベクトル

内分点と外分点とは
内分点におけるベクトル
外分点におけるベクトル
問題
まとめ

内分点と外分点とは

内分点と外分点について復習しよう！

● 線分 $AB$ を $m:n$ に内分する点 $P$

点 $P$ は $AP:PB=m:n$ を満たす

線分 $AB$ を線分の内側で分ける点だから「内分点」

● 線分 $AB$ を $m:n$ に外分する点 $Q$

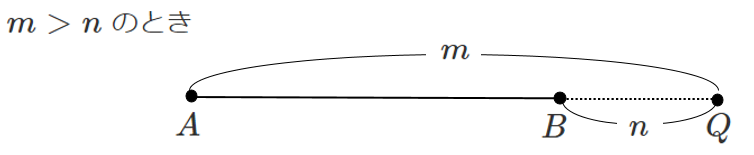
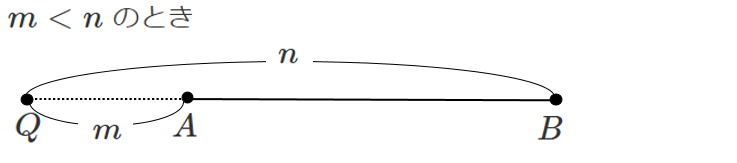
点 $Q$ は $AQ:QB=m:n$ を満たす

線分 $AB$ を線分の外側で分ける点だから「外分点」

　外分点は $m$ と $n$ の大小関係によって

　$A$ 側にとるか，$B$ 側にとるかが変わるので注意

内分点と外分点について詳しくはこれ↓

内分点と外分点

線分の内分点と外分点のとり方のポイント！外分点が苦手な人は必見！一筆書きで点がとれる！

内分点におけるベクトル

　$\triangle OAB$ において，$\overrightarrow{OA}=\vec{a}$，$\overrightarrow{OB}=\vec{b}$ とする。

　辺 $AB$ を $1:2$ に内分する点 $P$ について，$\overrightarrow{OP}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。

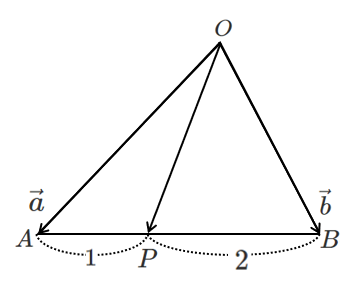
\begin{eqnarray} \overrightarrow{OP} &=& \overrightarrow{OA}+\overrightarrow{AP} \\\\ &=& \overrightarrow{OA}+\frac{1}{3}\overrightarrow{AB} \\\\ &=& \vec{a}+\frac{1}{3}(\vec{b}-\vec{a}) \\\\ &=& \frac{2}{3}\vec{a}+\frac{1}{3}\vec{b} \end{eqnarray}

毎回この計算をするのは大変なので一般化してみよう！

　$\triangle OAB$ において，$\overrightarrow{OA}=\vec{a}$，$\overrightarrow{OB}=\vec{b}$ とする。

　辺 $AB$ を $m:n$ に内分する点 $P$ について，$\overrightarrow{OP}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。

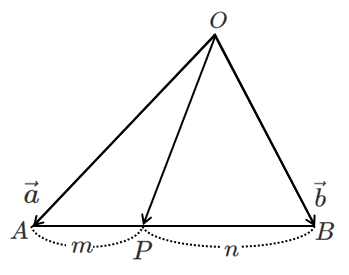
\begin{eqnarray} \overrightarrow{OP} &=& \overrightarrow{OA}+\overrightarrow{AP} \\\\ &=& \overrightarrow{OA}+\frac{m}{m+n}\overrightarrow{AB} \\\\ &=& \vec{a}+\frac{m}{m+n}(\vec{b}-\vec{a}) \\\\ &=& \frac{n}{m+n}\vec{a}+\frac{m}{m+n}\vec{b} \\\\ &=& \frac{n\vec{a}+m\vec{b}}{m+n} \end{eqnarray}

内分点におけるベクトル

　$\triangle OAB$ において，辺 $AB$ を $m:n$ に内分する点を $P$ とすると

$\displaystyle{\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}}$

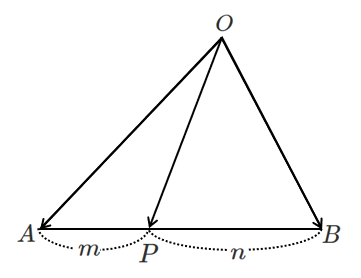
$\displaystyle{\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}}$

外分点におけるベクトル

外分点におけるベクトルも内分点と同様に考えることができる！

　$\triangle OAB$ において，$\overrightarrow{OA}=\vec{a}$，$\overrightarrow{OB}=\vec{b}$ とする。

　辺 $AB$ を $m:n$ に外分する点 $Q$ について，$\overrightarrow{OQ}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。

　$m>n$ のとき

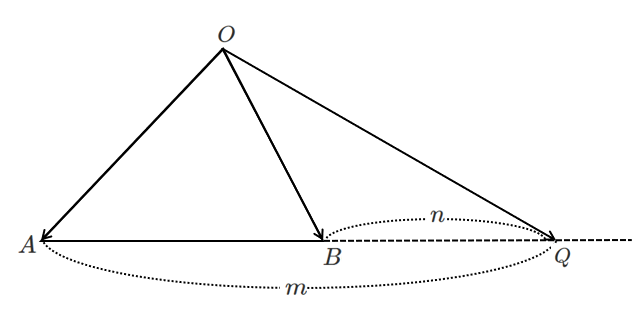
\begin{eqnarray} \overrightarrow{OQ} &=& \overrightarrow{OA}+\overrightarrow{AQ} \\\\ &=& \overrightarrow{OA}+\frac{m}{m-n}\overrightarrow{AB} \\\\ &=& \vec{a}+\frac{m}{m-n}(\vec{b}-\vec{a}) \\\\ &=& \frac{-n}{m-n}\vec{a}+\frac{m}{m-n}\vec{b} \\\\ &=& \frac{-n\vec{a}+m\vec{b}}{m-n} \end{eqnarray}

　$m<n$ のとき

外分点におけるベクトル

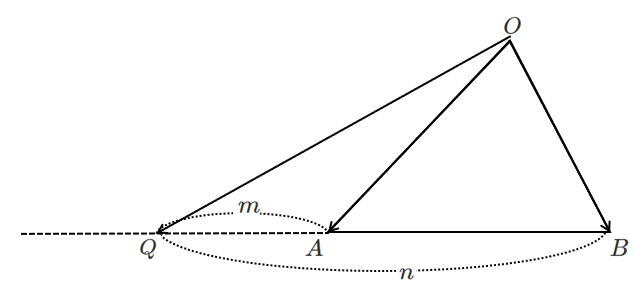
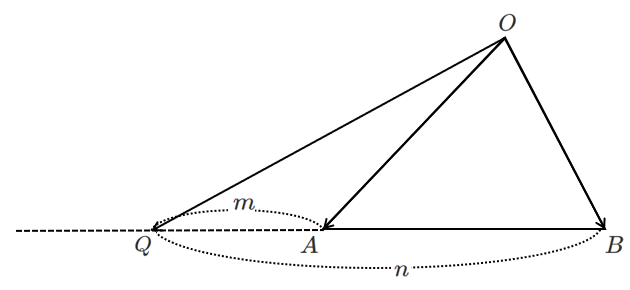
　$\triangle OAB$ において，辺 $AB$ を $m:n$ に外分する点を $Q$ とすると

$\displaystyle{\overrightarrow{OQ}=\frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}}$

$m>n$ のとき

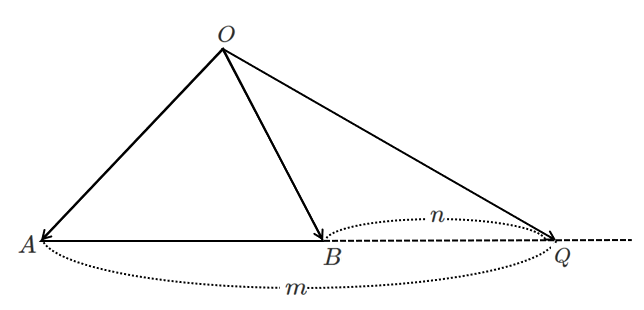
$m<n$ のとき

$\displaystyle{\overrightarrow{OQ}=\frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}}$

内分点と外分点の座標の式とよく似ているね！

よく気が付いたね！

内分は「足してクロス」

外分は「引いてクロス」

だったね！

問題

　$\triangle OAB$ において，辺 $AB$ を $3:2$ に内分する点を $C$，$3:1$ に外分する点を $D$，$2:3$ に外分する点を $E$ とする。$\overrightarrow{OA}=\vec{a}$，$\overrightarrow{OB}=\vec{b}$ とするとき，次のベクトルを $\vec{a}$，$\vec{b}$ を用いて表せ。

(1)　$\overrightarrow{OC}$

　点 $C$ は辺 $AB$ を $3:2$ に内分する点なので

\begin{eqnarray} \overrightarrow{OC} &=& \frac{2\overrightarrow{OA}+3\overrightarrow{OB}}{3+2} \\\\ &=& \frac{2}{5}\vec{a}+\frac{3}{5}\vec{b} \end{eqnarray}

(2)　$\overrightarrow{OD}$

　点 $D$ は辺 $AB$ を $3:1$ に内分する点なので

\begin{eqnarray} \overrightarrow{OD} &=& \frac{-\overrightarrow{OA}+3\overrightarrow{OB}}{3-1} \\\\ &=& -\frac{1}{2}\vec{a}+\frac{3}{2}\vec{b} \end{eqnarray}

(3)　$\overrightarrow{OE}$

　点 $E$ は辺 $AB$ を $2:3$ に内分する点なので

\begin{eqnarray} \overrightarrow{OE} &=& \frac{-3\overrightarrow{OA}+2\overrightarrow{OB}}{2-3} \\\\ &=& 3\vec{a}-2\vec{b} \end{eqnarray}

平行四辺形を題材とした問題も解いてみよう！

　平行四辺形 $ABCD$ において，対角線 $BD$ を $4:1$ に内分する点を $E$，辺 $BC$ を $1:3$ に内分する点を $F$ とする。$\overrightarrow{AB}=\vec{b}$，$\overrightarrow{AD}=\vec{d}$ とするとき，次のベクトルを $\vec{b}$，$\vec{d}$ を用いて表せ。

(1)　$\overrightarrow{AE}$

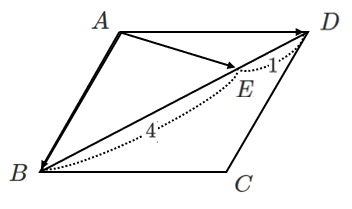
　点 $E$ は辺 $BD$ を $4:1$ に内分する点なので

\begin{eqnarray} \overrightarrow{AE} &=& \frac{\overrightarrow{AB}+4\overrightarrow{AD}}{4+1} \\\\ &=& \frac{1}{5}\vec{b}+\frac{4}{5}\vec{d} \end{eqnarray}

(2)　$\overrightarrow{AF}$

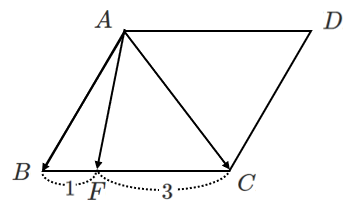
　$\overrightarrow{AC}=\vec{b}+\vec{d}$

　点 $F$ は辺 $BC$ を $1:3$ に内分する点なので

\begin{eqnarray} \overrightarrow{AF} &=& \frac{3\overrightarrow{AB}+\overrightarrow{AC}}{1+3} \\\\ &=& \frac{3}{4}\vec{b}+\frac{1}{4}(\vec{b}+\vec{d}) \\\\ &=& \vec{b}+\frac{1}{4}\vec{d} \end{eqnarray}

＜別解＞

\begin{eqnarray} \overrightarrow{AF} &=& \overrightarrow{AB}+\overrightarrow{BF} \\\\ \overrightarrow{AF} &=& \overrightarrow{AB}+\frac{1}{4}\overrightarrow{AD} \\\\ &=& \vec{b}+\frac{1}{4}\vec{d} \end{eqnarray}