高校数学で学ぶ『円と直線の位置関係と判別式』について解説!
円と直線の位置関係は、2次方程式の判別式で調べることができます!
この投稿を見れば、『円と直線の位置関係と判別式』についてバッチリ!
円と直線の位置関係

円と直線の位置関係は3パターン!
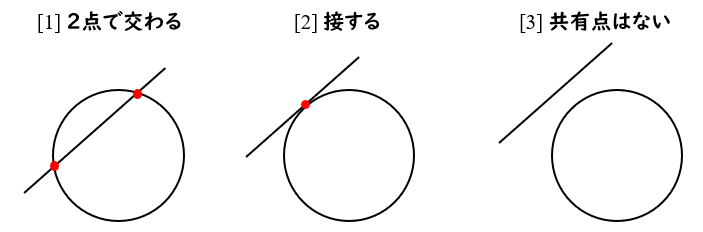
円と直線の共有点の個数
円と直線の共有点の求め方はこれ↓

[1] 2点で交わる場合
$
\left\{\begin{align}
&x^2+y^2=2 \cdots ①\\
&y=x \cdots ②
\end{align}\right.
$
②を①に代入して $x^2+x^2=2$
$2x^2=2$
$x^2=1$
$x=±1$
②より $x=1$ のとき $y=1$
$x=-1$ のとき $y=-1$
共有点の座標は $(1,1)$,$(-1,-1)$
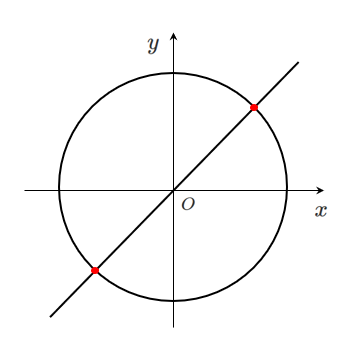
$y$ を消去した式 $x^2=1$ の実数解の個数が $2$ 個なので
共有点の個数も $2$ 個になる
[2] 接する(1点で交わる)場合
$
\left\{\begin{align}
&x^2+y^2=2 \cdots ①\\
&y=x-2 \cdots ②
\end{align}\right.
$
②を①に代入して $x^2+(x-2)^2=2$
$2x^2-4x+4=2$
$x^2-2x+1=0$
$(x-1)^2=0$
$x=1$
②より $y=-1$
共有点の座標は $(1,-1)$
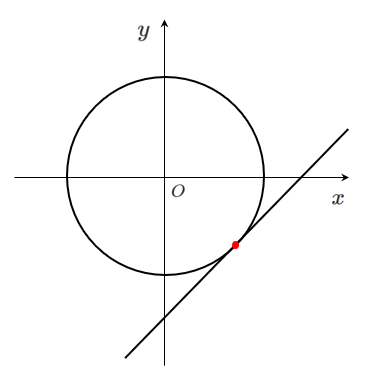
$y$ を消去した式 $x^2-2x+1=0$ の実数解の個数が $1$ 個なので
共有点の個数も $1$ 個になる
[3] 共有点がない場合
$
\left\{\begin{align}
&x^2+y^2=2 \cdots ①\\
&y=x-3 \cdots ②
\end{align}\right.
$
②を①に代入して $x^2+(x-3)^2=2$
$2x^2-6x+9=2$
$2x^2-6x+7=0$
この2次方程式の判別式を $D$ とすると
$D=(-6)^2-4\cdot2\cdot7=-20<0$
実数解をもたないので,共有点はない
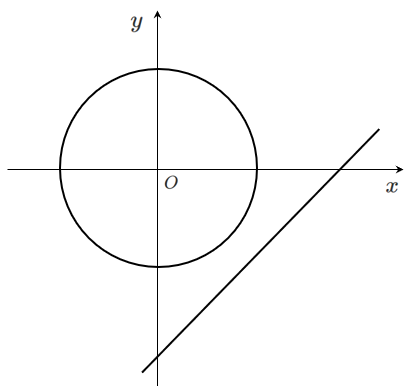
$y$ を消去した式 $2x^2-6x+7=0$ の実数解の個数が $0$ 個なので
共有点の個数も $0$ 個になる

$y$ を消去した $x$ の2次方程式の実数解の個数が共有点の個数と一致するね!
円と直線の共有点の個数は一致する

2次方程式の実数解の個数は,どうやって調べられる?

判別式 $D$ だね!

その通り!
円と直線の共有点の個数は $y$ を消去した2次方程式の判別式 $D$ を調べればわかるよ!
円と直線の位置関係と判別式

判別式 $D$ の復習をしよう!
$D>0$ のとき 異なる2つの実数解をもつ
$D=0$ のとき 重解をもつ(実数解1つ)
$D<0$ のとき 実数解をもたない
$y$ を消去した $x$ の2次方程式の実数解の個数と円と直線の共有点の個数は一致するので、
円と直線の共有点の個数は $y$ を消去した2次方程式の判別式で調べることができる
$D>0$ のとき 異なる2つの実数解をもつ ➡ 2点で交わる
$D=0$ のとき 重解をもつ(実数解1つ) ➡ 接する(1点で交わる)
$D<0$ のとき 実数解をもたない ➡ 共有点をもたない
よって、以下のことが成り立つ
円と直線の位置関係は以下のようになる
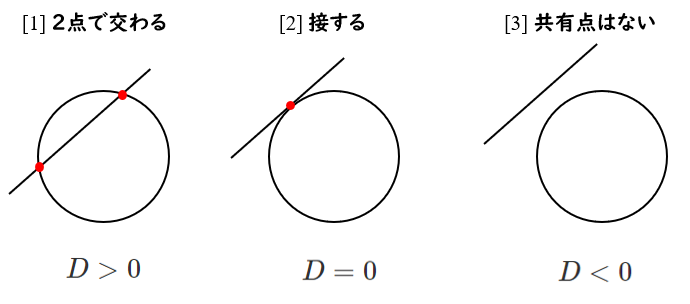
【補足】 共有点をもつときは $D≧0$
問題
$y=x+m$ を $x^2+y^2=2$ に代入して( $y$ 消去)
$x^2+(x+m)^2=2$
$2x^2+2mx+m^2-2=0$ $\cdots$ ①
2次方程式①の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=m^2-2(m^2-2)}$ $\displaystyle{\frac{D}{4}}$ について
$=-m^2+4$
円と直線が異なる2点で交わるとき,2次方程式①が異なる2つの実数解をもつので
$D>0$ より $-m^2+4>0$
$m^2-4<0$ ←不等号の向きに注意
$(m+2)(m-2)<0$
$-2<m<2$ 2次不等式が不安な人はこれ
また,そのときの接点の $x$ 座標を求めよ。
$y=x+m$ を $x^2+y^2=2$ に代入して
$x^2+(x+m)^2=2$
$2x^2+2mx+m^2-2=0$ $\cdots$ ①
2次方程式①の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=m^2-2(m^2-2)}=-m^2+4$
円と直線が接するとき,2次方程式①が重解をもつので
$D=0$ より $-m^2+4=0$
$m^2=4$
$m=±2$
2次方程式①について
$m=2$ のとき $2x^2+4x+2=0$
$(x+1)^2=0$
$x=-1$
$m=-2$ のとき $2x^2-4x+2=0$
$(x-1)^2=0$
$x=1$
まとめ
● 円と直線の位置関係と判別式
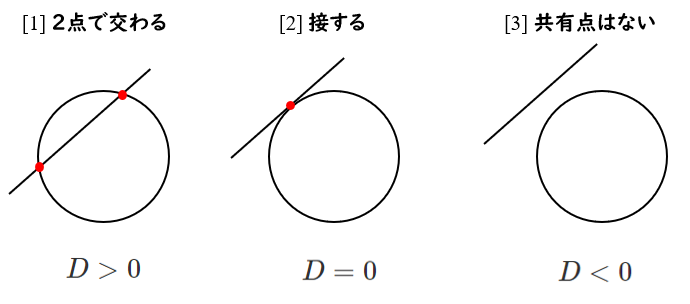
円と直線の方程式から $y$ を消去した2次方程式 $ax^2+bx+c=0$ の判別式を $D=b^2-4ac$ とすると
円と直線の位置関係は以下のようになる




コメント