円と直線の共有点の個数

高校数学で学ぶ『座標平面における円と直線の共有点の個数』について解説！

円と直線の共有点は連立方程式で求まる！

そして、円と直線の共有点の個数は、その計算過程で出てくる２次方程式の実数解の個数と一致する！

この投稿を見れば、『座標平面における円と直線の共有点の個数』の理解度が高まります！

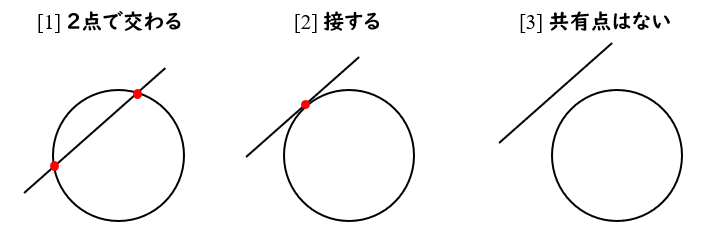
円と直線の位置関係

共有点の座標の求め方

$
\left\{\begin{align}
&y=x 　　　　\cdots ①\\
&y=-x+2　\cdots ②
\end{align}\right.
$

①を②に代入して　　$x=-x+2$
　　　　　　　　　　$2x=2$
　　　　　　　　　　　$x=1$
①に代入して　　$y=1$
したがって，共有点の座標は　$(1，1)$

　

円と直線の共有点の座標

[1] ２点で交わる場合

$
\left\{\begin{align}
&x^2+y^2=2　\cdots ①\\
&y=x　　　　\cdots ②
\end{align}\right.
$

②を①に代入して　　$x^2+x^2=2$
　　　　　　　　　　　　$2x^2=2$
　　　　　　　　　　　　$x^2=1$
　　　　　　　　　　　　　$x=±1$
②より　　$x=1$ のとき　$y=1$
　　　　　$x=-1$ のとき　$y=-1$
共有点の座標は　　$(1，1)$，$(-1，-1)$

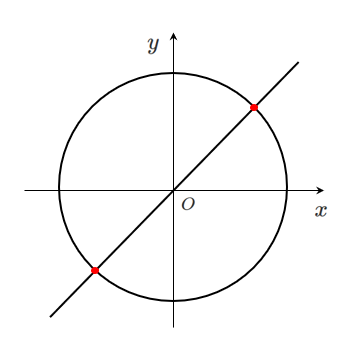
$y$ を消去した式 $x^2=1$ の実数解の個数が $2$ 個なので

共有点の個数も $2$ 個になる

[2] 接する（１点で交わる）場合

$
\left\{\begin{align}
&x^2+y^2=2　\cdots ①\\
&y=x-2　　　\cdots ②
\end{align}\right.
$

②を①に代入して　　$x^2+(x-2)^2=2$
　　　　　　　　　　　$2x^2-4x+4=2$
　　　　　　　　　　　$x^2-2x+1=0$
　　　　　　　　　　　　$(x-1)^2=0$
　　　　　　　　　　　　　　　$x=1$
②より　　$y=-1$
共有点の座標は　　$(1，-1)$

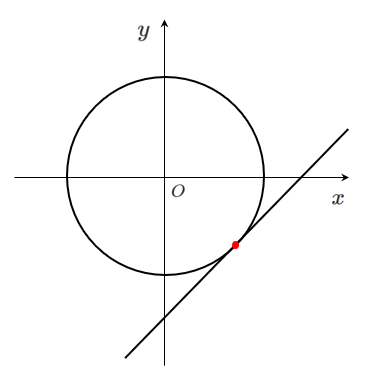
$y$ を消去した式 $x^2-2x+1=0$ の実数解の個数が $1$ 個なので

共有点の個数も $1$ 個になる

[3] 交わらない場合

$
\left\{\begin{align}
&x^2+y^2=2　\cdots ①\\
&y=x-3　　　\cdots ②
\end{align}\right.
$

②を①に代入して　　$x^2+(x-3)^2=2$
　　　　　　　　　　　$2x^2-6x+9=2$
　　　　　　　　　　　$2x^2-6x+7=0$
　　　　　　　　　　　　　　　$\displaystyle{x=\frac{3±\sqrt{5} i}{2}}$
実数解をもたないので，共有点はない

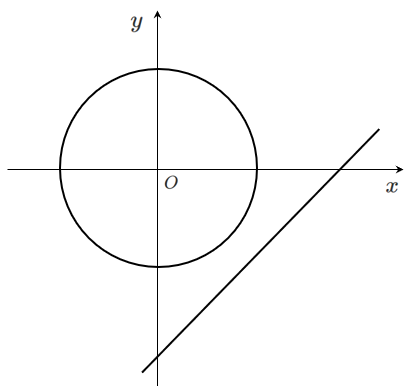
$y$ を消去した式 $2x^2-6x+7=0$ の実数解の個数が $0$ 個なので

共有点の個数も $0$ 個になる

　

　

まとめ

● 円と直線の位置関係

　[1] ２点で交わる
　[2] 接する（１点で交わる）
　[3] 交わらない

● 円と直線の共有点の座標の求め方

　連立方程式を解く

● 円と直線の共有点の個数

　$y$ を消去した $x$ の２次方程式の実数解の個数と円と直線の共有点の個数は一致する