多角形の外接円
多角形のすべての頂点が１つの円周上にあるとき
多角形の立場からすると，円の内側で接している！
円の立場からすると，多角形の外側で接している！
多角形と外接円
三角形の外接円の中心は「外心」で，辺の垂直二等分線の交点だったよね！
三角形の外心・内心・重心の復習はこれ↓
三角形の外心・内心・重心
三角形の外心・内心・重心がどういう点なのか、それぞれの特徴を整理しよう！
enjoy-mathematics.com
2022.12.17
円に内接する四角形
三角形には必ず外接円が存在するけど，四角形には存在するとは限らない！
「四角形の外接円が存在する」つまり「四角形が円に内接する」ときの性質について考えよう！
円に内接する四角形の性質
証明
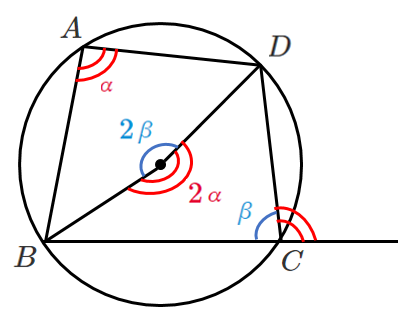
四角形 $ABCD$ が円 $O$ に接するとき
$\angle BAD=α$，$\angle BCD=β$ とする
円周角と中心角の関係より
$2α+2β=360°$
となるから $α+β=180°$
また $\angle BCD$ の外角は $180°-β=α$ となる
四角形が円に内接する条件
逆に四角形が円に内接するための条件はこれ！
四角形が円に内接する条件
対角の和が $180°$ なら四角形が円に内接するんだね！
まとめ
● 多角形と外接円
三角形には必ず外接円が存在する
三角形以外の多角形には外接円が存在するとは限らない
● 円に内接する四角形の性質
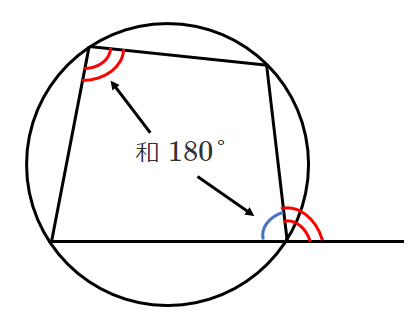
● 四角形が円に内接する条件
１組の対角の和が $180°$ または 内角が対角の外角と等しい
問題
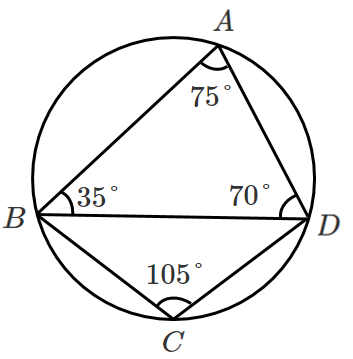
以下の図において，$α$ を求めよ。
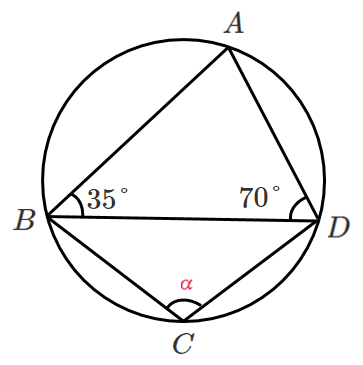
$\angle BAD=180°-(35°+70°)=75°$
$α+75°=180°$ より $α=105°$
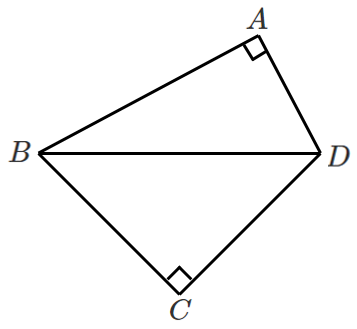
次の四角形 $ABCD$ のうち，円に内接するものはどちらか。
①
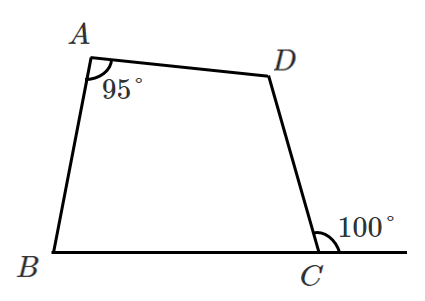
②
①は対角の和が $180°$ なので，円に内接する
②は内角 ($95°$) と対角の外角 ($100°$) が等しくないので，円に内接しない
よって 円に内接するのは①
数学Ⅰの三角比の問題でも使うことがあるから，しっかりおさえておこう！
コメント