高校数学Ⅱで学ぶ『原点を中心とする円の接線の方程式』について解説!
『円の接線の方程式』は忘れがちな公式の1つ!
接点が与えられている問題と与えられていない問題の2種類をマスターしましょう!
この投稿を見れば、『原点を中心とする円の接線の方程式』はバッチリ!
原点を中心とする円の接線の方程式
円 $x^2+y^2=r^2$ 上の点 $(p,q)$ における接線の方程式は
$px+qy=r^2$
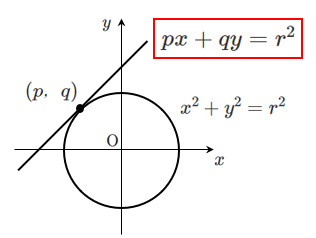
証明
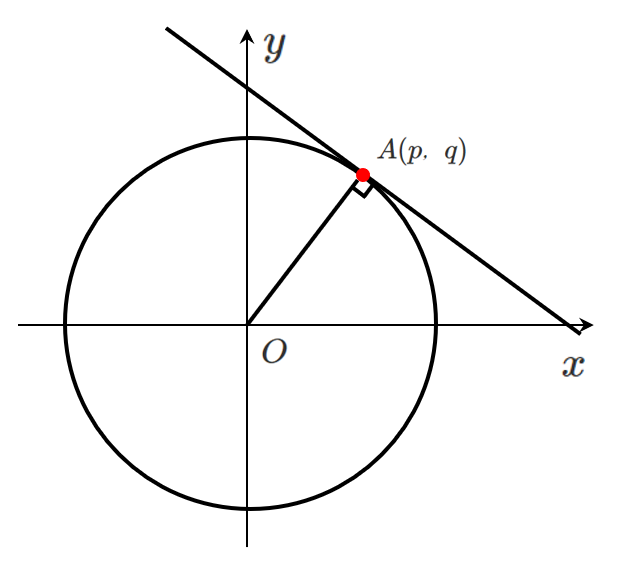
接点を $\textrm{A}(p,q)$ とする
直線 $\textrm{OA}$ の傾きは $\displaystyle{\frac{q}{p}}$
直線 $\textrm{OA}$ と接線は垂直なので,接線の傾きは $\displaystyle{-\frac{p}{q}}$ 垂直な直線
接線は傾き $\displaystyle{-\frac{p}{q}}$ で $(p,q)$ を通る直線なので
$\displaystyle{y-q=-\frac{p}{q}(x-p)}$ 直線の方程式
$\displaystyle{y-q=-\frac{p}{q}x-\frac{p^2}{q}}$
両辺に $q$ をかけると
$qy-q^2=-px+p^2$
$px+qy=p^2+q^2$
ここで,点 $(p,q)$ は円 $x^2+y^2=r^2$ 上にあるので
$p^2+q^2=r^2$
接線の方程式は $px+qy=r^2$

・原点が中心の円
・接点の座標が分かっている
場合しか使えないので注意!
覚え方
➡ $px+qy=r^2$
接点が与えられている問題
(1) 円 $x^2+y^2=5$ 接点 $(2,1)$
(2) 円 $x^2+y^2=10$ 接点 $(1,-3)$
(1) $2x+y=5$
(2) $x-3y=10$
接点が与えられていない問題
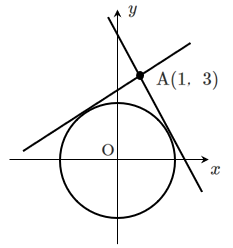
解答1:接点の座標をおく
接点の座標を $(p,q)$ とおくことで,接線の方程式が $px+qy=5$ と表せる
[1] 接線 $px+qy=5$ が点 $\textrm{A}(1,3)$ を通る
[2] 接点 $(p,q)$ が円 $x^2+y^2=5$ 上にある
という2つの条件から $p$ と $q$ の方程式を2つ作る
接点の座標を $(p,q)$ とすると,接線の方程式は $px+qy=5$ … ①
$(1,3)$ を通るから $p+3q=5$ … ②
$(p,q)$ は円周上の点であるから $p^2+q^2=5$ … ③
②より $p=-3q+5$
これを③に代入して $(-3q+5)^2+q^2=5$
$q^2-3q+2=0$
これを解いて $q=1,2$
②に代入して $q=1$ のとき $p=2$
$q=2$ のとき $p=-1$
求める接線方程式は①に代入して $2x+y=5$,$-x+2y=5$
解答2:直線の方程式を表してdとr
点 $\textrm{A}(1,3)$ を通るので,傾きを $m$ とおくと $y-3=m(x-1)$ と表せる
※ 傾きを文字でおく場合,$y$ 軸に平行な直線は表せないので,
「求める接線が $y$ 軸に平行な直線 $x=3$ でない」ことを記述しておく必要がある
円と直線が接する場合,「円の中心と直線の距離 $d$ と円の半径 $r$ が等しい」という式が作れる
【参考:円と直線の位置関係とd、rの大小】
点 $\textrm{A}(1,3)$ を通り,$y$ 軸に平行な直線 $x=3$ はこの円の接線ではないから,
求める接線の傾きを $m$ とすると $y-3=m(x-1)$
すなわち $mx-y-m+3=0$ … ①
円の中心である原点と直線①の距離を $d$ とすると
$\displaystyle{d=\frac{|-m+3|}{\sqrt{m^2+(-1)^2}}=\frac{|-m+3|}{\sqrt{m^2+1}}}$
直線①がこの円の接線となるとき,$d$ の値は円の半径と等しいので
$\displaystyle{\frac{|-m+3|}{\sqrt{m^2+1}}=\sqrt{5}}$
$|-m+3|=\sqrt{5(m^2+1)}$
両辺を2乗すると $(-m+3)^2=5(m^2+1)$
$2m^2+3m-2=0$
$(m+2)(2m-1)=0$
$\displaystyle{m=-2,\frac{1}{2}}$
求める接線の方程式は①に代入して $-2x-y+5=0$,$\displaystyle{\frac{1}{2}x-y+\frac{5}{2}=0}$
したがって $2x+y=5$,$-x+2y=5$
解答3:直線の方程式を表して判別式
点 $\textrm{A}(1,3)$ を通るので,傾きを $m$ とおくと $y-3=m(x-1)$ と表せる
※ 傾きを文字でおく場合,$y$ 軸に平行な直線は表せないので,
「求める接線が $y$ 軸に平行な直線 $x=3$ でない」ことを記述しておく必要がある
円と直線が接する場合,
「円の方程式と直線の方程式で $y$ を消去した2次方程式の判別式 $D=0$」
【参考:円と直線の位置関係と判別式D】
点 $(1,3)$ を通り,$y$ 軸に平行な直線 $x=3$ はこの円の接線ではないから,
求める接線の傾きを $m$ とすると $y-3=m(x-1)$
すなわち $y=m(x-1)+3$
$x^2+y^2=5$ と連立して,$y$ を消去すると
$x^2+\{m(x-1)+3\}^2=5$
$(m^2+1)x^2-2m(m-3)x+(m^2-6m+4)=0$
直線が円に接するから,この方程式は重解をもつ
判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=\{-m(m-3)\}^2-(m^2+1)(m^2-6m+4)}$
$=(m^4-6m^3+9m^2)-(m^4-6m^3+5m^2-6m+4)$
$=4m^2+6m-4$
$=2(m+2)(2m-1)$
$D=0$ より $\displaystyle{m=-2,\frac{1}{2}}$
求める接線の方程式は①に代入して $-2x-y+5=0$,$\displaystyle{\frac{1}{2}x-y+\frac{5}{2}=0}$
したがって $2x+y=5$,$-x+2y=5$
まとめ
● 円の接線と接線
● 円の接線の方程式
円 $x^2+y^2=r^2$ 上の点 $(p,q)$ における接線の方程式は
$px+qy=r^2$
簡単にすると
円 $x^2+y^2=○$ 上の点 $(□,△)$ における接線の方程式は
$□x+△y=○$

円の接線の方程式の公式を使いこなせるようになろう!




コメント