命題の逆・裏・対偶の整理できていますか?
どれがどれだっけ?という人は必見です!
もとの命題とその対偶の真偽が一致するという性質を用いて,
命題の真偽を考える問題も重要!
この投稿を見れば,命題の逆・裏・対偶は完璧!
条件の否定

条件の否定を復習しよう!
条件の否定はこれ↓

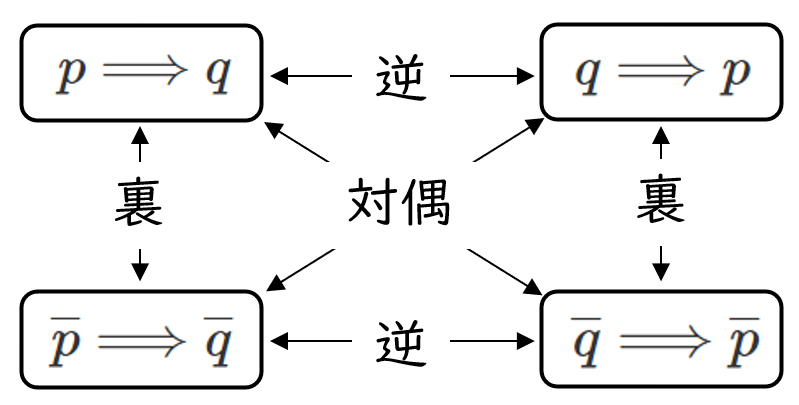
命題 $p\Longrightarrow q$ の逆・裏・対偶
逆 $q\Longrightarrow p$(逆にする)
裏 $\overline{p}\Longrightarrow \overline{q}$(否定する)
対偶 $\overline{q}\Longrightarrow \overline{p}$(逆にして否定する)
命題の対偶とその真偽
条件 $p$ を満たす集合全体を $P$
条件 $q$ を満たす集合全体を $Q$ とすると
命題 $p\Longrightarrow q$ が真であることは
$P⊂Q$ であることと同じである
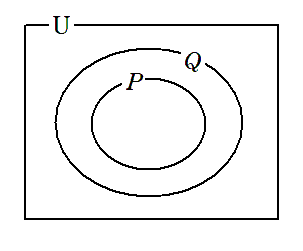
このとき $\overline{Q}⊂\overline{P}$ が成り立つので
$\overline{q}\Longrightarrow \overline{p}$ は真である
よって
命題 $p\Longrightarrow q$ が真であることは
$\overline{q}\Longrightarrow \overline{p}$ は真であることと同じ
偽のときも同様に言える

命題の真偽の判定が難しいときは
対偶をとって真偽の判定をすることができるよ!
まとめ
● 命題 $p\Longrightarrow q$ の逆・裏・対偶
逆 $q\Longrightarrow p$(逆にする)
裏 $\overline{p}\Longrightarrow \overline{q}$(否定する)
対偶 $\overline{q}\Longrightarrow \overline{p}$(逆にして否定する)

● 命題 $p\Longrightarrow q$ とその対偶 $\overline{q}\Longrightarrow \overline{p}$ の真偽は一致する
問題
次の命題の逆,裏,対偶を求めよ。
また,対偶の真偽を調べてもとの命題の真偽を答えよ。
(1) $x+y<0$ $\Longrightarrow $ $x<0$ または $y<0$
(2) $mn$ は奇数 $\Longrightarrow $ $m,n$ はともに奇数
解答
(1) $x+y<0$ $\Longrightarrow $ $x<0$ または $y<0$
逆 $x<0$ または $y<0$ $\Longrightarrow $ $x+y<0$
裏 $x+y≧0$ $\Longrightarrow $ $x≧0$ かつ $y≧0$
対偶 $x≧0$ かつ $y≧0$ $\Longrightarrow $ $x+y≧0$
対偶は真なので、もとの命題も真である
(2) $mn$ は奇数 $\Longrightarrow $ $m,n$ はともに奇数
逆 $m,n$はともに奇数 $\Longrightarrow $ $mn$ は奇数
裏 $mn$ は偶数 $\Longrightarrow $ $m,n$ の少なくとも一方が偶数
対偶 $m,n$の少なくとも一方が偶数 $\Longrightarrow $ $mn$ は偶数
対偶が真なので、もとの命題は真である
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント