命題の真偽の判定を自信をもってできますか?
命題の真偽の判定は,非常に重要です!
例えば,頻出である「必要条件と十分条件」の問題を解くときに,命題の真偽の判定は必要不可欠です!
苦手な人が多い命題の真偽の判定ですが,集合を使えば誰でも簡単にできます!
命題とは
命題 … 正しいか正しくないかが定まる文や式
命題の例
- $2$ は素数である 正しい
- $\sqrt{3}-\sqrt{2}=1$ である 正しくない
- 正三角形は二等辺三角形である 正しい

「シグにゃんはかわいい」は命題かな?

僕はかわいいと思うけど、
かわいくないと思う人もいるかもしれないから、
命題じゃないね!

悲しい…
人によって正しいか正しくないかが分かれるものは
命題とは言わないよ!
命題が正しいとき,その命題は真
命題が正しくないとき,その命題は偽
であるという
命題 $p\Longrightarrow q$
命題 $p\Longrightarrow q$ ( $p$ ならば $q$ とよむ )
$p$ を仮定、$q$ を結論という
命題 $p\Longrightarrow q$ が真になる場合
「命題 $p\Longrightarrow q$ は真である」ことは
「 $p$ を満たすものはすべて $q$ を満たす 」こと
このことを集合で表してみる
条件 $p$ を満たす全体の集合を $P$
条件 $q$ を満たす全体の集合を $Q$
とすると
「命題 $p\Longrightarrow q$ は真である」ことは
「 $P$ の要素はすべて $Q$ の要素になる 」こと
すなわち $P⊂Q$( $P$ は $Q$ に含まれる)
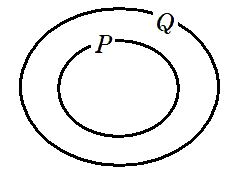
「$⊂$」の記号が分からないときはこれ↓

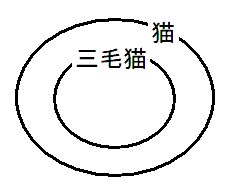
● $三毛猫\Longrightarrow 猫$ の真偽
$三毛猫⊂猫$ なので
$三毛猫\Longrightarrow 猫$ は真である
命題 $p\Longrightarrow q$ が偽になる場合
「命題 $p\Longrightarrow q$ は偽である」ことは
「 $p$ を満たすが $q$ を満たさないものが存在する 」こと
$p$ を満たすが $q$ を満たさないものを反例という
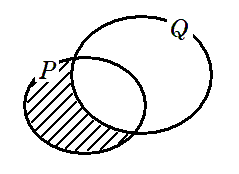
● $猫\Longrightarrow 三毛猫$ の真偽
猫の中には三毛猫以外にもペルシャ猫が存在する
つまり,ペルシャ猫という反例が存在するので
$猫\Longrightarrow 三毛猫$ は偽である
まとめ
命題 … 正しいか正しくないかが定まる文や式
命題が正しいとき、その命題は真
命題が正しくないとき、その命題は偽
命題 $p\Longrightarrow q$ ( $p$ ならば $q$ とよむ )
$p$ を仮定、$q$ を結論という
条件 $p$ を満たす全体の集合を $P$
条件 $q$ を満たす全体の集合を $Q$ としたとき
「命題 $p\Longrightarrow q$ は真である」ことは
「 $P⊂Q$($P$ は $Q$ に含まれる)である」ことと同じ
反例が見つかれば 命題 $p\Longrightarrow q$ は偽である
問題
$a,b$ は実数,$n$ は自然数とする。
次の命題の真偽を調べ,偽のときは反例を1つ示せ。
(1) $a=2$ $\Longrightarrow $ $a^2=4$
(2) $n$ が偶数 $\Longrightarrow $ $n$ が $4$ の倍数
(3) $a>1$ $\Longrightarrow $ $a>0$
(4) $ab=0$ $\Longrightarrow $ $a=0$
(1) $a=2$ $\Longrightarrow $ $a^2=4$
$a=2$ $\Longrightarrow $ $a=±2$
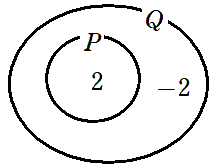
$2$ を要素にもつ集合を $P$
$±2$ を要素にもつ集合を $Q$ とすると
$P⊂Q$ が成り立つので
$a=2$ $\Longrightarrow$ $a^2=4$ は真である
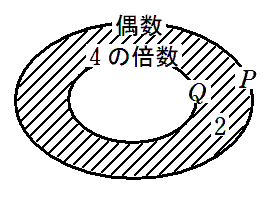
(2) $n$ が偶数 $\Longrightarrow $ $n$ が $4$ の倍数
偶数である数全体の集合を $P$
$4$ の倍数である数全体の集合を $Q$ とすると
$P⊃Q$ が成り立つので
$n$ が偶数 $\Longrightarrow $ $n$ が $4$ の倍数 は偽である
反例は $n=2$( $2$ は偶数だけど $4$ の倍数ではない)
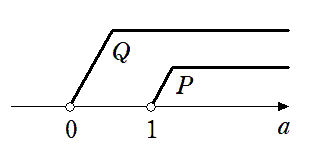
(3) $a>1$ $\Longrightarrow $ $a>0$
$a>1$ を満たす $a$ の値全体の集合を $P$
$a>0$ を満たす $a$ の値全体の集合を $Q$ とすると
$P⊂Q$ が成り立つので
$a>1$ $\Longrightarrow $ $a>0$ は真である
(4) $ab=0$ $\Longrightarrow $ $a=0$
$ab=0$ を解くと $a=0$ または $b=0$
すなわち $ab=0$ は必ずしも $a=0$ でなくてもよい
$a=1,b=0$ という反例が存在するので
$ab=0$ $\Longrightarrow $ $a=0$ は偽である

集合の関係を使って真偽の判定ができるようになろう!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント