場合の数
ある事柄の起こり方が何通りかを求めることを
「場合の数を求める」という
数学におけるある事柄とは,具体的に
- さいころを投げたときの目の出方
- コインを投げたときの裏表の出方
- 袋に入っている玉の取り出し方
などが挙げられる
樹形図

場合の数を「もれなく」「だぶりなく」求める方法として,
まずは「樹形図」を学ぼう!
引き分けはなく,$3$ 勝したらそれ以降の試合はないものとする。
$1$ 試合目に勝利したとき,予選を通過するための勝敗の順は何通りか。
樹形図をかくと
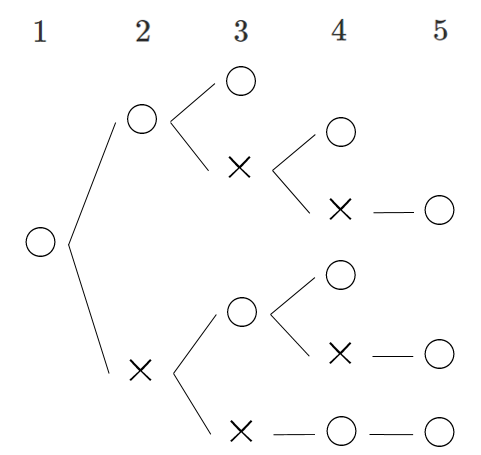
求める場合の数は $6$ 通り

「もれなく」「だぶりなく」数えたいときは
「樹形図」が分かりやすいね!
和の法則
$A$ または $B$ の起こる場合の数は,$a+b$ 通り
3つ以上の事柄についても同様

和の法則は簡単に言うと
「重複していないなら足せる」という法則だよ!
$5$ の倍数になる目の出方は何通りか。
目の和が $5$ の倍数になるのは
目の和が $5$ または $10$ のときである
[1] 目の和が $5$ のとき
$(1,4)$,$(2,3)$,$(3,2)$,$(4,1)$ の $4$ 通り
[2] 目の和が $10$ のとき
$(4,6)$,$(5,5)$,$(6,4)$ の $3$ 通り
[1] と [2] の起こり方に重複はないので
$4+3=7$ (通り)
※さいころの目の出方を $(大,小)$ と表している

「同時に起こらない」ことは「足す」
積の法則
$A$ が起こり,$B$ が起こる場合は $a×b$ 通り
3つ以上の事柄についても同様

「積の法則」を理解するには「樹形図」が効果的だよ!
全部で何通り種類のセットができるか。
①ライスかパン
②唐揚げかハンバーグかトンカツ
樹形図で表すと

①の選び方 $2$ 通りのそれぞれに対して,
②の選び方が $3$ 通りあるから
$2×3=6$ (通り)

「樹形図」をかくと「積の法則」が理解しやすいね!

3つ以上の事柄に対しても「積の法則」は使えるよ!
全部で何通り種類のセットができるか。
①ライスかパン
②味噌汁かコーンポタージュ
③唐揚げかハンバーグかトンカツ
樹形図で表すと
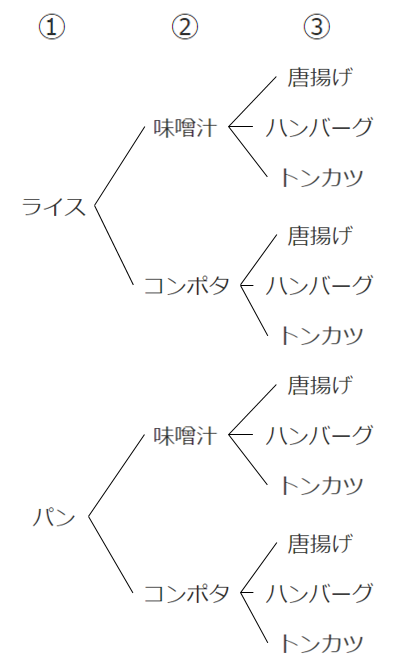
①の選び方 $2$ 通りのそれぞれに対して,
②の選び方は $2$ 通りで $2×2$ (通り)
①,②の選び方 $2×2$ 通りのそれぞれに対して,
③の選び方は $3$ 通りなので,
$2×2×3=12$ (通り)

「樹形図」を考えれば,
「積の法則」が使える理由も納得!
まとめ
● 場合の数を求めるポイント
「もれなく」かつ「だぶりなく(重複なく)」数える(計算する)こと
樹形図を作ると考えやすい
● 和の法則
2つの事柄に $A$ ($a$ 通り) と $B$ ($b$ 通り) に重複がないとき
$A$ または $B$ の起こる場合の数は,$a+b$ 通り
3つ以上の事柄についても同様
● 積の法則(樹形図を考えることが大切)
事柄 $A$ の $a$ 通りのどの場合に対しても事柄 $B$ が$b$ 通りあれば,
$A$ が起こり,$B$ が起こる場合は $a×b$ 通り
3つ以上の事柄についても同様
問題
(1) 2個のさいころの目の出方
(2) 目の和が $4$ の倍数
(3) 大きいさいころは偶数,小さいさいころは $3$ の倍数
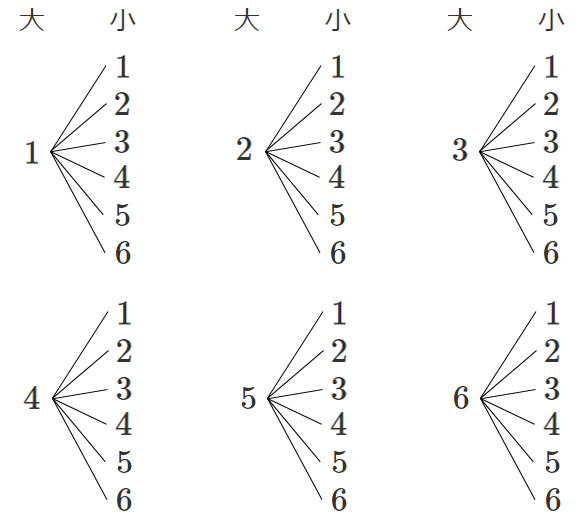
(1) 2個のさいころの目の出方
大のさいころの目の出方は $6$ 通り
その出方それぞれに対して小さいさいころの目の出方は $6$ 通り
積の法則より $6×6=36$ (通り)
(2) 目の和が $4$ の倍数
目の和が $4$ の倍数になるのは
目の和が $4$ または $8$ または $12$ のときである
[1] 目の和が $4$ のとき
$(1,3)$,$(2,2)$,$(3,1)$ の $3$ 通り
[2] 目の和が $8$ のとき
$(2,6)$,$(3,5)$,$(4,4)$,$(5,3)$,$(6,2)$ の $5$ 通り
[3] 目の和が $12$ のとき
$(6,6)$
[1] と [2] と [3] の起こり方に重複はないので
和の法則より $3+5+1=9$ (通り)
※さいころの目の出方を $(大,小)$ と表している
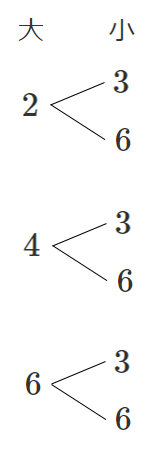
(3) 大きいさいころは偶数,小さいさいころは $3$ の倍数
大のさいころの目の出方は,$2$,$4$,$6$ の $3$ 通り
その出方それぞれに対して小さいさいころの目の出方は,$3$,$6$ の $2$ 通り
積の法則より $3×2=6$ (通り)

「和の法則」と「積の法則」を使い分けられるようにしよう!




コメント