絶対値記号のはずし方の基本

絶対値ってそもそも何だっけ?

絶対値は「原点からの距離を表す記号」だよ!
絶対値の基本は下のリンクから学べるよ!

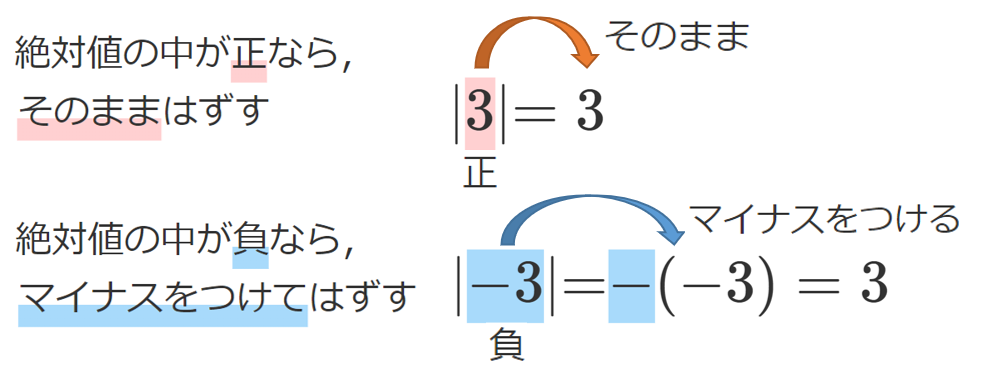

絶対値の中の符号が分かれば,絶対値をはずすことができるよ!
場合分けによる絶対値記号のはずし方
(1) $|x-1|$
(2) $|2x+4|$
(2) $|3-x|$

絶対値の中に $x$ が含まれているから,絶対値の中の符号がわからない…

こういうときに必要なのが『場合分け』だよ!
絶対値の中が『正のとき』と『負のとき』で場合分けしよう!
(1) $|x-1|$
絶対値の中 $x-1$ が正($0$ 以上)のとき
$x-1≧0$ すなわち $x≧1$ のとき
$|x-1|=x-1$
(そのままはずす)
絶対値の中 $x-1$ が負のとき
$x-1<0$ すなわち $x < 1$ のとき
$|x-1|=-(x-1)=-x+1$
(マイナスをつけてはずす)
まとめると
\begin{align} &|x-1|=\left\{ \begin{array}{ll} x-1 (x≧1 のとき) \\ -x+1 (x<1 のとき) \end{array} \right.\\\\ \end{align}(2) $|2x+4|$
絶対値の中 $2x+4$ が正($0$ 以上)のとき
$2x+4≧0$ すなわち $x≧-2$ のとき
$|2x+4|=2x+4$
(そのままはずす)
絶対値の中 $2x+4$ が負のとき
$2x+4<0$ すなわち $x < -2$ のとき
$|2x+4|=-(2x+4)=-2x-4$
(マイナスをつけてはずす)
まとめると
\begin{align} &|2x+4|=\left\{ \begin{array}{ll} 2x+4 (x≧-2 のとき) \\ -2x-4 (x<-2 のとき) \end{array} \right.\\\\ \end{align}(3) $|3-x|$
絶対値の中 $3-x$ が正($0$ 以上)のとき
$3-x≧0$ すなわち $x≦3$ のとき
$|3-x|=3-x$
(そのままはずす)
絶対値の中 $3-x$ が負のとき
$3-x<0$ すなわち $x > 3$ のとき
$|3-x|=-(3-x)=-3+x$
(マイナスをつけてはずす)
まとめると
\begin{align} &|3-x|=\left\{ \begin{array}{ll} 3-x (x≦3 のとき) \\ -3+x (x>3 のとき) \end{array} \right.\\\\ \end{align}
場合分けによる絶対値記号のはずし方【2つ】

絶対値が2つになったら,問題が少し複雑になるよ!
$$|x+1|+|x-2|$$
$|x+1|$ と $|x-2|$ の絶対値をはずすと以下のようになる
\begin{align} &|x+1|=\left\{ \begin{array}{ll} x+1 (x≧-1 のとき) \\ -x-1 (x<-1 のとき) \end{array} \right.\\\\ \end{align} \begin{align} &|x-2|=\left\{ \begin{array}{ll} x-2 (x≧2 のとき) \\ -x+2 (x<2 のとき) \end{array} \right.\\\\ \end{align} $|x+1|$ は $-1$ を境に場合分け
$|x-2|$ は $2$ を境に場合分け
これらの場合分けを1つの数直線にまとめると
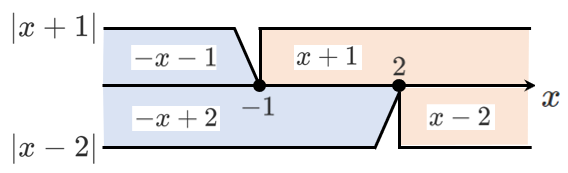
このように $-1$ と $2$ を境に,3つのパターンで場合分けすることができます
$x < -1$ のとき
$|x+1|=-x-1$,$|x-2|=-x+2$ なので
$-1 ≦ x < 2$ のとき
$|x+1|=x+1$,$|x-2|=-x+2$ なので
$2 ≦ x$ のとき
$|x+1|=x+1$,$|x-2|=x-2$ なので
まとめると
\begin{align} &|x+1|+|x-2|=\left\{ \begin{array}{lll} -2x+1 (x<-1 のとき) \\ 3 (-1 ≦ x < 2 のとき) \\ 2x-1 (2≦x のとき) \end{array} \right. \end{align}

絶対値が複数個ある場合は,
それぞれの絶対値を場合分けして
1つの数直線にまとめるのがポイントだね!
絶対値のはずし方まとめ
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント