
定積分を用いて2つの曲線の間の面積を求める方法を学ぼう!
定積分
$F'(x)=f(x)$ のとき
$\displaystyle{\int_a^b f(x) dx=\left[F(x)\right]_a^b=F(b)-F(a)}$
定積分の $\displaystyle{\int_a^b f(x) dx}$ において
$a$ を 下端(かたん),$b$ を 上端(じょうたん) という
定積分の $\displaystyle{\int_a^b f(x) dx}$ を求めることを
関数 $f(x)$ を $a$ から $b$ まで 積分する という
定積分の計算についてはこれ↓
2https://enjoy-mathematics.com/%e5%ae%9a%e7%a9%8d%e5%88%86/
定積分と面積

定積分を用いれば,曲線で囲まれる面積を求めることができる!
$a≦x≦b$ において,$f(x)≧0$ のとき(関数 $y=f(x)$ が $x$ 軸より上側のとき)
関数 $y=f(x)$,2直線 $x=a$,$x=b$,$x$ 軸で囲まれる部分の面積 $S$ は
$\displaystyle{S=\int_a^b f(x) dx}$
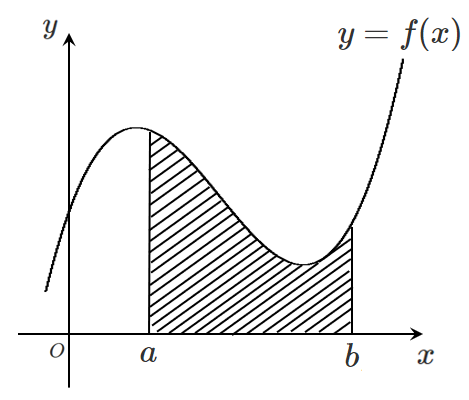
関数 $y=f(x)$ が $x$ 軸より上側にあるときは
$\displaystyle{S=\int_a^b f(x) dx}$
2つの曲線の間の面積
$a≦x≦b$ の範囲で $f(x)≧g(x)$ のとき( $f(x)$ が $g(x)$ より上側のとき)
$y=f(x)$ と $y=g(x)$ のグラフおよび2直線 $x=a,x=b$ で囲まれた部分の面積 $S$ は
$\displaystyle{S=\int_a^b \left\{f(x)-g(x)\right\} dx}$
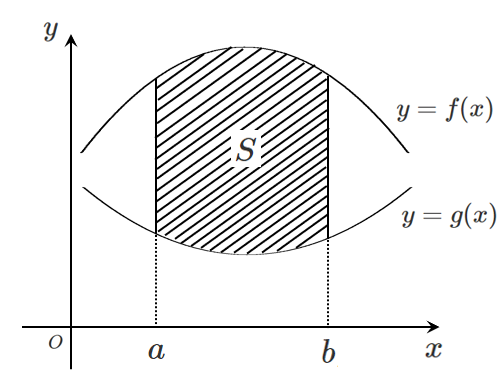
$f(x)$ が $g(x)$ より上側にあるとき
$\displaystyle{S=\int_a^b \left\{f(x)-g(x)\right\} dx}$
問題1
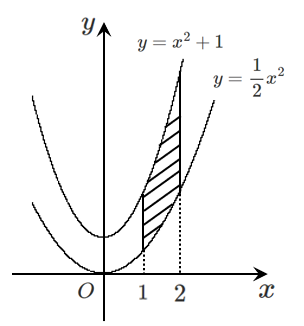
問題2

放物線と直線で囲まれた部分の面積!
放物線 $y=x^2$ と直線 $y=-x+2$ の共有点の $x$ 座標は
$x^2=-x+2$
$x^2+x-2=0$
$(x-1)(x+2)=0$
$x=1,-2$
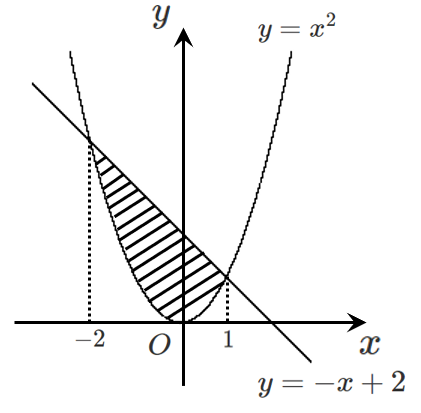
問題3

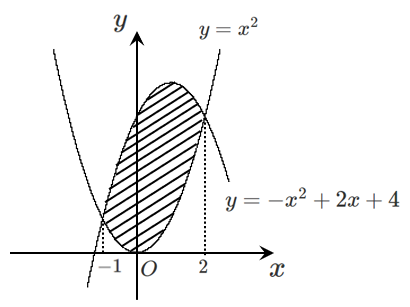
放物線と放物線で囲まれた部分の面積!
放物線 $y=x^2$ と放物線 $y=-x^2+2x+4$ の共有点の $x$ 座標は
$x^2=-x^2+2x+4$
$2x^2-2x-4=0$
$x^2-x-2=0$
$(x-2)(x+1)=0$
$x=-1,2$
まとめ
● 2曲線の間の面積

$f(x)$ が $g(x)$ より上側にあるとき
$\displaystyle{S=\int_a^b \left\{f(x)-g(x)\right\} dx}$

(上の関数ー下の関数)で積分したら面積が求まる!




コメント