
3次関数と $x$ 軸で囲まれる部分の面積の求め方を学ぼう!
3次関数のグラフ

まずは,3次関数のグラフの形について学ぼう!
増減表をかくとグラフの形がわかる!
極値がある場合の3次関数 $y=ax^3+bx^2+cx+d$ のグラフは
$a>0$ のとき
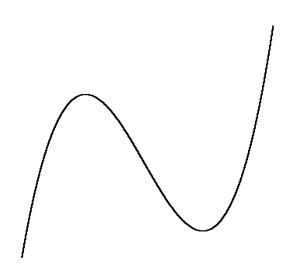
$a<0$ のとき
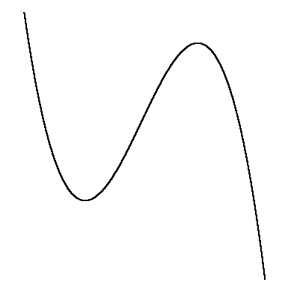

具体例をみてみよう!
導関数 $f'(x)$ を求めると
$f'(x)=3x^2-6x=3x(x-2)$
$f'(x)=0$ を求めると
$3x(x-2)=0$
$x=0,2$
$f'(x)$ のグラフをかくと
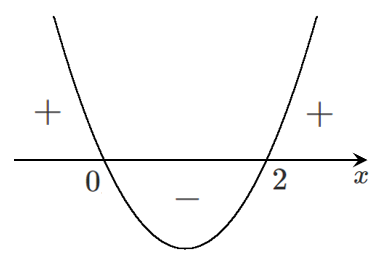
増減表をかくと
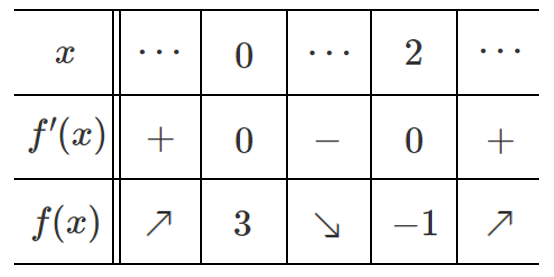
したがって
$x=0$ で極大値 $3$
$x=2$ で極小値 $-1$
グラフは
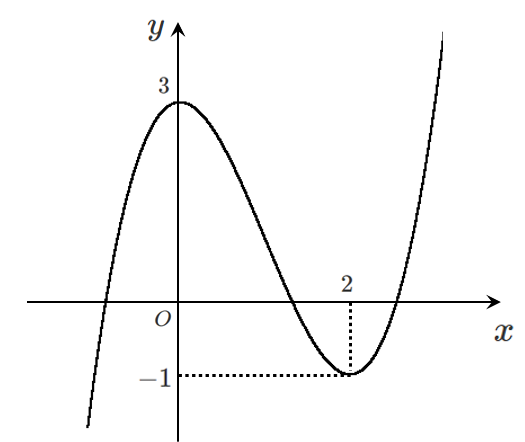
導関数 $f'(x)$ を求めると
$f'(x)=-3x^2+6x=-3x(x-2)$
$f'(x)=0$ を求めると
$-3x(x-2)=0$
$x=0,2$
$f'(x)$ のグラフをかくと
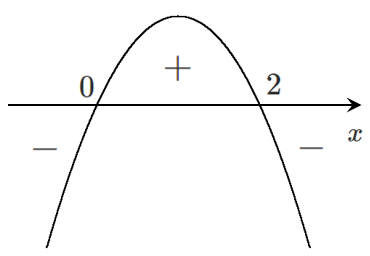
増減表をかくと
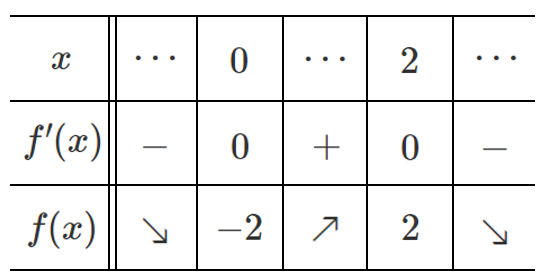
したがって
$x=2$ で極大値 $2$
$x=0$ で極小値 $-2$
グラフは
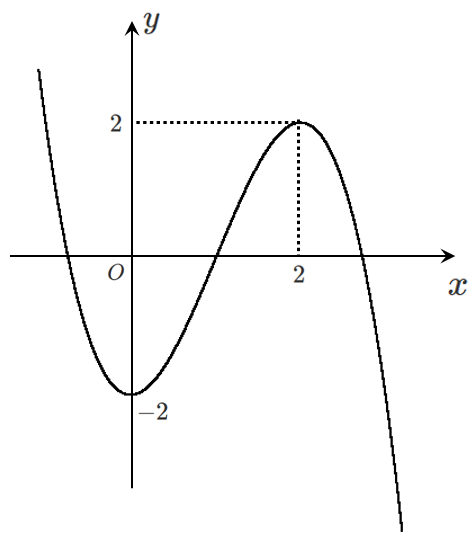

$x^3$ の係数の符号でグラフの形は決まる!
3次関数の増減表とグラフはこれ↓

定積分と面積
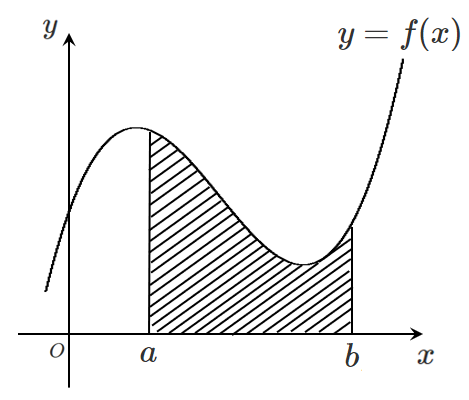
関数 $y=f(x)$ が $x$ 軸より上側にあるときは
$\displaystyle{S=\int_a^b f(x) dx}$
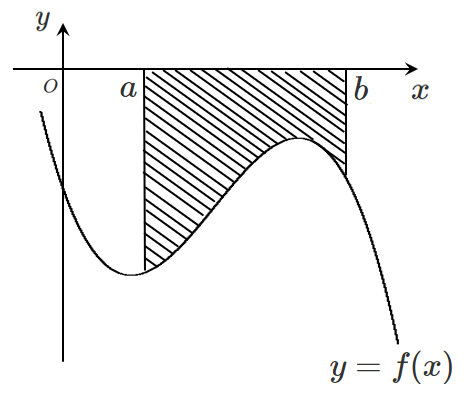
関数 $y=f(x)$ が $x$ 軸より下側にあるときは
$\displaystyle{S=\int_a^b \left\{-f(x)\right\} dx}$

定積分で面積を求めるときに気を付けることは,$x$ 軸より上か下か!
定積分と面積について詳しくはこれ↓

3次関数と面積

3次関数と $x$ 軸で囲まれた部分の面積を求めよう!
問題1
3次関数 $y=x^3-3x^2+2x$ と $x$ 軸の共有点は $y=0$ を代入して
$x^3-3x^2+2x=0$
$x(x^2-3x+2)=0$
$x(x-1)(x-2)=0$
$x=0,1,2$
$x^3$ の係数は正なので,グラフの形は

$x$ 軸と $x=0,1,2$ で交わるので
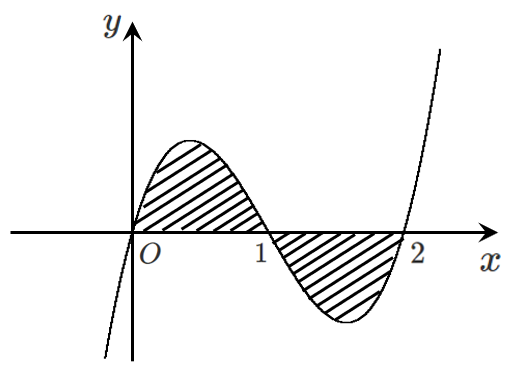
$0≦x≦1$ で $y≧0$(グラフは $x$ 軸より上側)
$1≦x≦2$ で $y≦0$(グラフは $x$ 軸より下側)
求める面積 $S$ は
\begin{align} S&=\int_0^1 (x^3-3x^2+2x) dx +\int_1^2 \left\{-(x^3-3x^2+2x)\right\} dx \\\\ \end{align}$x$ 軸より上側と下側の部分を分けて定積分して足す
計算すると
\begin{align} S&=\int_0^1 (x^3-3x^2+2x) dx +\int_1^2 \left\{-(x^3-3x^2+2x)\right\} dx \\\\ &= \left[ \frac{1}{4}x^4-x^3+x^2 \right]_0^1 + \left[ -\frac{1}{4}x^4+x^3-x^2 \right]_1^2 \\\\ &= \frac{1}{4}\cdot1^4-1^3+1^2-\frac{1}{4}(2^4-1^4)+(2^3-1^3)-(2^2-1^2) \\\\ &= \frac{1}{4}-\frac{15}{4}+7-3 \\\\ &= \frac{1}{2} \\\\ \end{align}問題2
3次関数 $y=-x^3+x$ と $x$ 軸の共有点は $y=0$ を代入して
$-x^3+x=0$
$-x(x^2-1)=0$
$x(x-1)(x+1)=0$
$x=0,1,-1$
$x^3$ の係数は負なので,グラフの形は

$x$ 軸と $x=0,1,-1$ で交わるので
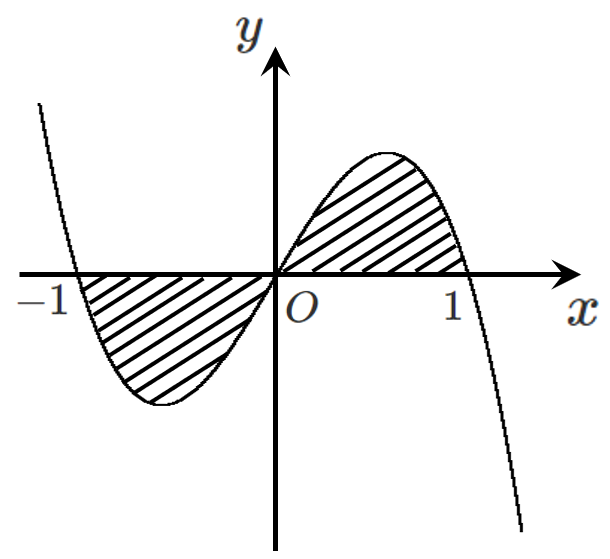
$-1≦x≦0$ で $y≦0$(グラフは $x$ 軸より下側)
$0≦x≦1$ で $y≧0$(グラフは $x$ 軸より上側)
求める面積 $S$ は
\begin{align} S&=\int_-1^0 \left\{-(-x^3+x)\right\} dx +\int_0^1 (-x^3+x) dx \\\\ &= \left[ \frac{1}{4}x^4-\frac{1}{2}x^2 \right]_{-1}^0 + \left[ -\frac{1}{4}x^4+\frac{1}{2}x^2 \right]_0^1 \\\\ &= -\left\{\frac{1}{4}\cdot(-1)^4-\frac{1}{2}\cdot(-1)^2\right\}-\frac{1}{4}\cdot 1^4+\frac{1}{2}\cdot1^2 \\\\ &= -\frac{1}{4}+\frac{1}{2}+\frac{1}{4}+\frac{1}{2} \\\\ &= 1 \\\\ \end{align}問題3
3次関数 $y=-x^3+x$ と $x$ 軸の共有点は $y=0$ を代入して
$x^3-2x^2-x+2=0$
$P(x)=x^3-2x^2-x+2$ とすると,$P(1)=0$ より
$P(x)$ は $x-1$ を因数にもつので,組み立て除法を用いて
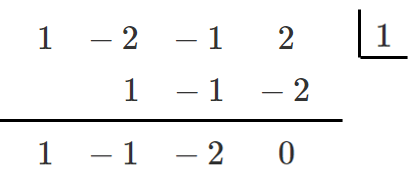
$(x-1)(x^2-x-2)=0$
$(x-1)(x+1)(x-2)=0$
$x=1,-1,2$
因数定理を用いた3次式の因数分解についてはこれ↓
3次関数 $y=x^3-2x^2-x+2$ と $x$ 軸と $x=1,-1,2$ で交わるので
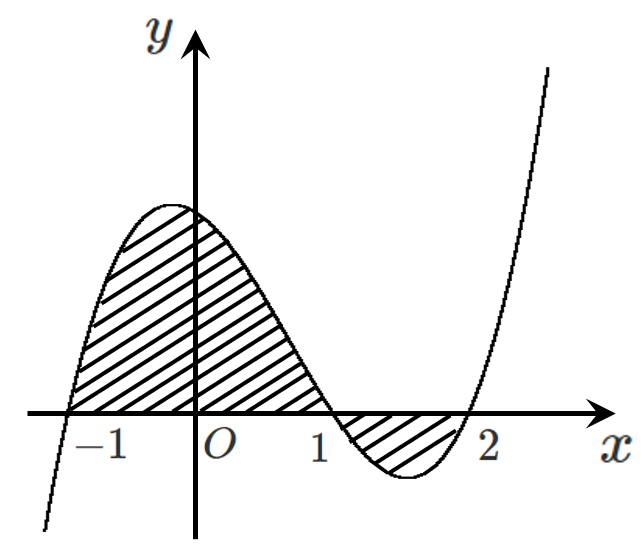
$-1≦x≦1$ で $y≧0$(グラフは $x$ 軸より上側)
$1≦x≦2$ で $y≦0$(グラフは $x$ 軸より下側)
求める面積 $S$ は
\begin{align} S&=\int_{-1}^1 (x^3-2x^2-x+2) dx +\int_1^2 \left\{-(x^3-2x^2-x+2)\right\} dx \\\\ &= \left[ \frac{1}{4}x^4-\frac{2}{3}x^3-\frac{1}{2}x^2+2x \right]_{-1}^1 + \left[ -\frac{1}{4}x^4+\frac{2}{3}x^3+\frac{1}{2}x^2-2x \right]_1^2 \\\\ &= \frac{1}{4}\left\{1^4-(-1)^4\right\}-\frac{2}{3}\left\{1^3-(-1)^3\right\}-\frac{1}{2}\left\{1^2-(-1)^2\right\}+2\left\{1-(-1)\right\}-\frac{1}{4}(2^4-1^4)+\frac{2}{3}(2^3-1^3)+\frac{1}{2}(2^2-1^2)-2(2-1) \\\\ &= -\frac{4}{3}+4-\frac{15}{4}+\frac{14}{3}+\frac{3}{2}-2 \\\\ &= \frac{37}{12} \\\\ \end{align}まとめ
● 3次関数のグラフ
極値がある場合の3次関数 $y=ax^3+bx^2+cx+d$ のグラフは
$a>0$ のとき

$a<0$ のとき

● 定積分と面積
関数 $y=f(x)$ が $x$ 軸より上側にあるときは
$\displaystyle{S=\int_a^b f(x) dx}$

関数 $y=f(x)$ が $x$ 軸より下側にあるときは
$\displaystyle{S=\int_a^b \left\{-f(x)\right\} dx}$


図がかけたら,$x$ 軸の上側と下側で分けて定積分するだけ!
計算ミスに注意!




コメント