実数

実数とは何か？聞かれたら困る人は必見！

実数，有理数，無理数，…‥

数学には○○数というものが多く登場します。

「○○数っていっぱいあるけど，どれがどれかわからない」

という中学生・高校生のために，

『実数』『有理数』『無理数』を分かりやすく教えます！

わかってしまえば，『実数』『有理数』『無理数』なんて簡単！

これを読んだら，問題文に○○数というキーワードがあっても大丈夫！

　

実数・有理数・無理数とは

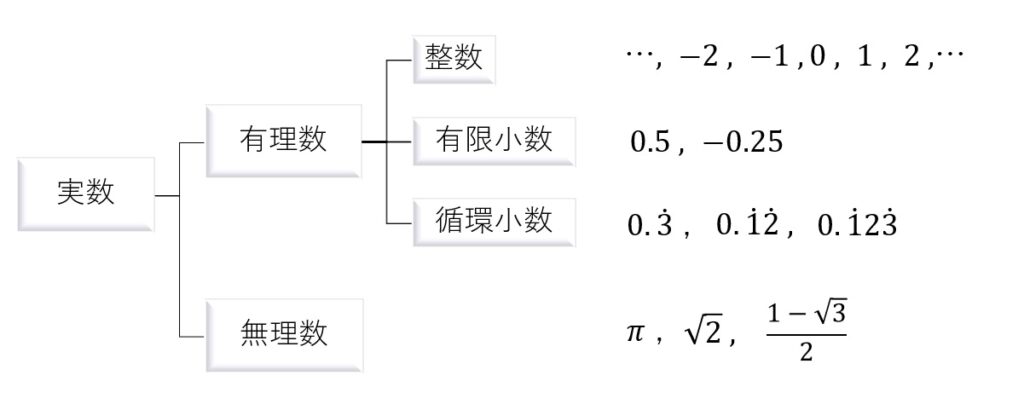
実数【Real number】…現実世界に存在する数（数直線上にとれる！）

有理数…分数で表すことができる数

無理数…分数で表すことができない数（分数にするのが無理！）

有理数

循環小数

$$0.333\cdots\cdots=0.\dot{3}$$

$$0.121212\cdots\cdots=0.\dot{1}\dot{2}$$

$$0.123123123\cdots\cdots=0.\dot{1}2\dot{3}$$

　以上のように、同じ数字が無限に循環するような小数のことを循環小数という

循環小数を分数で表す

　$x=0.333\cdots$　　$\cdots\cdots$　①　とする

　両辺を 10 倍すると　 $10x=3.333\cdots\cdots$　　$\cdots\cdots$　②

　②－①を計算すると

\begin{eqnarray} 　10x &=& 3.333\cdots\cdots \\ -\large{)}　x &=& 0.333\cdots\cdots \\ \hline 9x &=& 3 \\ x &=& \frac{1}{3} \end{eqnarray}

　したがって，　　$\displaystyle{0.\dot{3}=\frac{1}{3}}$
　

　$x=0.121212 \cdots$　　$\cdots\cdots$　① 　とする

　両辺を 100 倍すると　 $100x=12.121212 \cdots$　　$\cdots\cdots$　②

　②－①を計算すると

\begin{eqnarray} 　100x &=& 12.121212\cdots\cdots \\ -\large{)}　x &=&\;\;0.121212\cdots\cdots \\ \hline 99x &=& 12 \\ x &=& \frac{12}{99} \\ &=& \frac{4}{33} \end{eqnarray}

　したがって，　　　$\displaystyle{0.\dot{1}\dot{2}=\frac{4}{33}}$

　

　$x=0.123123123 \cdots$　　$\cdots\cdots$　① 　とする

　両辺を 1000 倍すると　 $1000x=123.123123123 \cdots$　　$\cdots\cdots$　②

　②－①を計算すると

\begin{eqnarray} 　1000x &=& 123.123123123\cdots\cdots \\ -\large{)}　x &=&\;\;\;\;0.123123123\cdots\cdots \\ \hline 999x &=& 123 \\ x &=& \frac{123}{999} \\ &=& \frac{41}{333} \end{eqnarray}

　したがって，　　　 $\displaystyle{0.\dot{1}2\dot{3}=\frac{41}{333}}$

　

無理数

　　　$\pi=3.14159265359$…
　　　円周率・・・円の直径に対する円周の長さ

　　　$\sqrt{2}=1.41421356$…（一夜一夜に人見頃）
　　　$2$ 乗したら $2$ になる正の数

　　　$\sqrt{3}=1.7320508$…（人並みにおごれや）
　　　$2$ 乗したら $3$ になる正の数

　　　$\sqrt{5}=2.2360679$…（富士山麓オウム鳴く）
　　　$2$ 乗したら $5$ になる正の数

　このように規則性もなく無限に続く小数のことを循環しない無限小数という

　規則性がないから語呂合わせがあると考えよう

　循環しない無限小数は，

循環小数のように分数で表すことができない

　ので，無理数に分類される

　また，

$\displaystyle{\frac{1-\sqrt{3}}{2}}$ や $\displaystyle{\frac{\pi}{4}}$

　のような数も無理数に分類される

実数

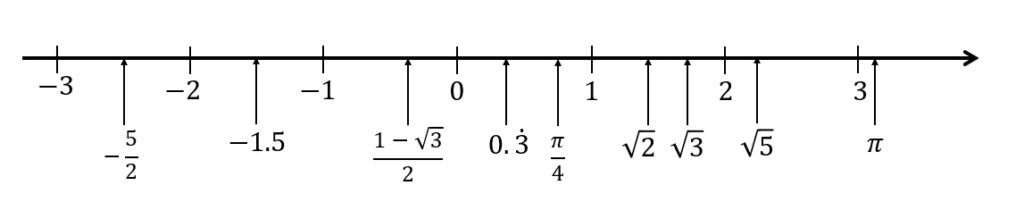
　有理数と無理数は必ず数直線上にとることができる

　逆に，数直線上にとることができない数を虚数という

まとめ

実数【Real number】…現実世界に存在する数（数直線上にとれる！）

有理数…分数で表すことができる数

無理数…分数で表すことができない数（分数にするのが無理！）

問題

問題の解答

　

　有理数　　$\displaystyle{\frac{3}{5}}$　　$-0.2$　　$\sqrt{4}$　　$0.\dot{2}$

　無理数　　$\sqrt{2}+1$　　$\displaystyle{\frac{\pi}{8}}$

　

　

(1)　

　$x=0.111 \cdots$　　$\cdots\cdots$　①　とする

　両辺を 10 倍すると　 $10x=1.111 \cdots$　　$\cdots\cdots$　②

　②－①を計算すると

\begin{eqnarray} 　10x &=& 1.111\cdots\cdots \\ -\large{)}　x &=& 0.111\cdots\cdots \\ \hline 9x &=& 1 \\ x &=& \frac{1}{9} \end{eqnarray}

　したがって，　　　$\displaystyle{0.\dot{1}=\frac{1}{9}}$

　

(2)

　$x=0.151515 \cdots$　　$\cdots\cdots$　① 　とする

　両辺を 100 倍すると　 $100x=15.151515 \cdots$　　$\cdots\cdots$　②

　②－①を計算すると　　

\begin{eqnarray} 　100x &=& 15.151515\cdots\cdots \\ -\large{)}　x &=&\;\;0.151515\cdots\cdots \\ \hline 99x &=& 15 \\ x &=& \frac{15}{99} \\ &=& \frac{5}{33} \end{eqnarray}

　したがって，　　　　$\displaystyle{0.\dot{1}\dot{5}=\frac{5}{33}}$

　

　

🔰基本…まずはこの記事から！
🔵標準…基本問題や公式の理解度が重要！
🔴応用…場合分けなど思考力が要求される！