命題の証明方法の一つとして「対偶を利用した証明」があります!
「対偶を利用した証明」はどんな問題で有効で,どういう手順で証明するのかを解説しました!
この投稿を見れば,「対偶を利用した証明」を確実に理解できます!
対偶とは
命題 $p\Longrightarrow q$ の対偶は $\overline{q}\Longrightarrow \overline{p}$ (命題を逆にして否定する)である。
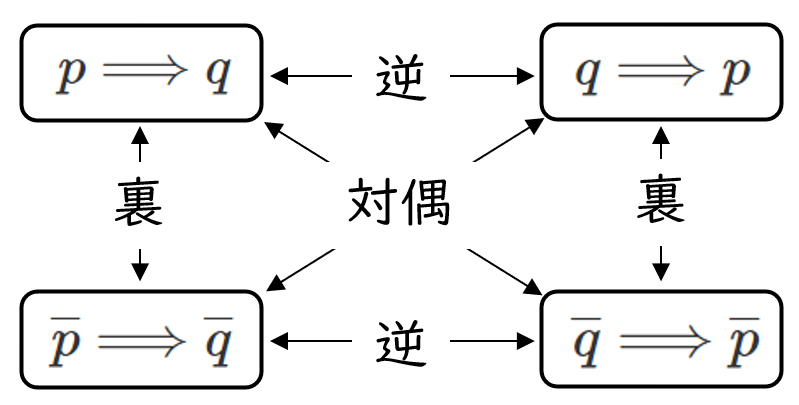

『対偶』のポイントはこれ!
対偶の復習はこれ↓

対偶を利用した証明を使う場面

どんなときに対偶を利用して証明すればいいのかな?

『もとの命題とその対偶は真偽が一致する』ので,
直接証明しにくい問題は,対偶を利用して証明するのが有効だよ!
直接証明しにくい命題は,対偶を利用して証明する
対偶を利用した証明

直接証明しにくい問題ってどんな問題?

問題を見てみよう!
結論が仮定より単純な命題
$n^2$ が偶数ならば,$n$ は偶数である

命題「$n^2$ が偶数 $\Longrightarrow$ $n$ が偶数」は
仮定より結論の方が次数が低いので
対偶「$n$ が奇数 $\Longrightarrow$ $n^2$ が奇数」の方が証明しやすい!
【証明】
もとの命題の対偶「$n$ が奇数ならば,$n^2$ は奇数である」を証明する
$n$ が奇数であるとき,整数 $k$ を用いて $n=2k+1$ と表せるから
$n^2=(2k+1)^2=2(2k^2+2k)+1$
$k$ は整数より,$2k^2+2k$ も整数であるから,$n^2$ は奇数である
よって,対偶が証明されたからもとの命題も成り立つ
● $2\times$(整数)$+1$ の形で表せる数は奇数
● 『$2k^2+2k$ は整数であるから』は必ず書く
結論が「○または○」「少なくとも一方は」という形の命題
$mn$ が偶数ならば,$m$ または $n$ は偶数である

結論の「$m$ または $n$ が偶数」というのは,
(ア) $m$ が偶数,$n$ が偶数
(イ) $m$ が偶数,$n$ が奇数
(ウ) $m$ が奇数,$n$ が偶数
の3つの場合があって扱いにくいので,対偶をとる!

対偶は「$m$ が奇数 かつ $n$ が奇数ならば,$mn$ は奇数」
だから考えやすくなるね!
【証明】
もとの命題の対偶「$m$ が奇数 かつ $n$ が奇数ならば,$mn$ は奇数である」を証明する
$m$,$n$ は整数であるとき,整数 $k$,$l$ を用いて $m=2k+1$,$n=2l+1$ と表されるから
$mn=(2k+1)(2l+1)=2(2kl+k+l)+1$
$k$,$l$ は奇数より,$2kl+k+l$ も整数であるから,$mn$ は奇数である
よって,対偶が証明されたから,もとの命題も成り立つ
「○または○」の否定の復習はこれ↓

$m^2+n^2$ が奇数ならば,$m$,$n$ の少なくとも一方は偶数である

結論の「$m$,$n$ の少なくとも一方は偶数」というのは,
(ア) $m$ が偶数,$n$ が偶数
(イ) $m$ が偶数,$n$ が奇数
(ウ) $m$ が奇数,$n$ が偶数
の3つの場合があって扱いにくいので,対偶をとる!

対偶は「$m$,$n$ がともに奇数ならば,$m^2+n^2$ は偶数」
だから考えやすくなるね!
【証明】
もとの命題の対偶「$m$,$n$ がともに奇数ならば,$m^2+n^2$ は奇数である」を証明する
$m$,$n$ は奇数であるとき,整数 $k$,$l$ を用いて $m=2k+1$,$n=2l+1$ と表されるから
$m^2+n^2=(2k+1)^2+(2l+1)^2=2(2k^2+2k+2l^2+2l+1)$
$k$,$l$ は整数より,$2k^2+2k+2l^2+2l+1$ も整数であるから,$m^2+n^2$ は偶数である
よって,対偶が証明されたから,もとの命題も成り立つ
「少なくとも一方は〇」の否定の復習はこれ↓

まとめ
●命題の対偶とその真偽
命題 $p\Longrightarrow q$ とその対偶 $\overline{q}\Longrightarrow \overline{p}$ の真偽は一致する
●対偶を利用した証明を使う場面
もとの命題とその対偶は真偽が一致するので,
直接証明しにくい命題は,対偶を利用して証明する
具体的に
1.結論が仮定より単純な命題
2.結論が「○または○」「少なくとも一方は」という命題
が挙げられる
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント