2次関数でよく出題される計算といったら『平方完成』
『平方完成』は2次関数の『軸』と『頂点』を求める大切な計算!
2次関数の大問の最初にする計算なので,間違えないことが必要不可欠!
x以外の文字が含まれる場合の『平方完成』もおさえておこう!
これを見れば,『平方完成』はばっちり!

数字だけだったら平方完成ができるんだけど、$x$ 以外の文字が含まれたら分からなくなるよ…

$x$ 以外の文字が含まれる2次関数の平方完成をマスターしよう!
平方完成とは

平方完成ってそもそも何?

平方完成とは2次関数 $y=ax^2+bx+c$ を $y=a(x-p)^2+q$ という形に変形することだよ!
なぜ平方完成をするのか

2次関数の軸や頂点を求めたいときに平方完成をするよ!
2次関数 $y=ax^2+bx+c$ は放物線
放物線には,『下に凸』と『上に凸』という形がある
$a > 0$ のとき
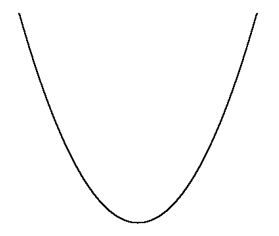
下に凸
$a > 0$ のとき
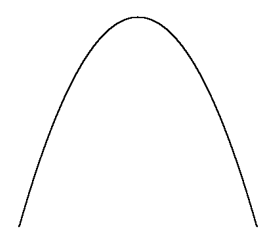
上に凸
放物線の位置を決めるものとして,『軸』と『頂点』がある
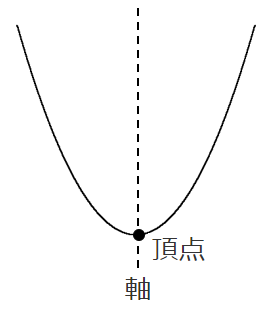
$y=ax^2+bx+c$ の形のままでは『軸』と『頂点』が分からない
$y=a(x-p)^2+q$ という形に式変形することで,『軸』と『頂点』が分かる
すなわち,平方完成することで『軸』と『頂点』が分かる
$y=a(x-p)^2+q$
軸 直線 $x=p$
頂点 $(p,q)$

2次関数の問題は初めに平方完成をさせる問題がほとんどだから、きちんと計算できるようにしよう!
平方完成の準備
因数分解の公式 $x^2-2ax+a^2=(x-a)^2$ を式変形した
$x^2-2ax=(x-a)^2-a^2$
を用いると平方完成ができます。
$x^2-$$2a$$x$
↓半分
$=(x-$$a$$)^2-$$a^2$
|___↑2乗を引く

平方完成の手順
- $x^2$ の係数でくくる
- かっこの中で $( )^2$ を作る
- $\{ \}$ を展開する
平方完成
例題 次の2次関数を平方完成し、頂点を求めよ。
(1) $y=x^2-2ax-2$
(2) $y=ax^2+2ax-2$
(3) $y=x^2-2(a-1)x+1$
(1)
$y=x^2-$$2a$$x-2$
↓半分
$ =(x-$$a$$)^2-$$a^2$$-2$
|__↑2乗を引く
$ =(x-a)^2-a^2-2$
頂点は $(a,-a^2-2)$
(2)
$y=ax^2+2ax-2$
$ =a(x^2+$$2$$x)-2$ ← $x^2$ の係数でくくる
↓半分
$ =a\{(x+$$1$$)^2-$$1^2$$\}-2$ ← かっこの中で $( )^2$ を作る
|__↑2乗を引く
$ =a(x+1)^2-a-2$ ← $\{ \}$ を展開する
$ =a(x+1)^2-a-2$
頂点は $(-1,-a-2)$
(3)
$y=x^2-$$2(a-1)$$x+1$
↓半分
$ =\{x-$$(a-1)$$\}^2-$$(a-1)^2$$+1$
|_______↑2乗を引く
$ =\{x-(a-1)\}^2-(a^2-2a+1)+1$
$ =\{x-(a-1)\}^2-a^2+2a$
頂点は $(a-1,-a^2+2a)$
まとめ
●平方完成の準備
$x^2-$$2a$$x$
↓半分
$=(x-$$a$$)^2-$$a^2$
|___↑2乗を引く
●平方完成の手順
- $x^2$ の係数でくくる
- かっこの中で $( )^2$ を作る
- $\{ \}$ を展開する
●2次関数の頂点
$y=a(x-p)^2+q$
頂点 $(p,q)$
問題
問題 次の2次関数を平方完成し、頂点を求めよ。
(1) $y=x^2+2ax-1$
(2) $y=ax^2-2ax+1$
(3) $y=x^2-2(a+1)x+1$
解答
(1)
$y=x^2+$$2a$$x-1$
↓半分
$ =(x+$$a$$)^2-$$a^2$$-1$
|__↑2乗を引く
$ =(x+a)^2-a^2-1$
頂点は $(-a,-a^2-1)$
(2)
$y=ax^2-2ax+1$
$ =a(x^2-$$2$$x)+1$ ← $x^2$ の係数でくくる
↓半分
$ =a\{(x-$$1$$)^2-$$1^2$$\}+1$ ← かっこの中で $( )^2$ を作る
|__↑2乗を引く
$ =a(x-1)^2-a+1$ ← $\{ \}$ を展開する
$ =a(x-1)^2-a+1$
頂点は $(1,-a+1)$
(3)
$y=x^2-$$2(a+1)$$x+1$
↓半分
$ =\{x-$$(a+1)$$\}^2-$$(a+1)^2$$+1$
|_______↑2乗を引く
$ =\{x-(a+1)\}^2-(a^2+2a+1)+1$
$ =\{x-(a+1)\}^2-a^2-2a$
頂点は $(a+1,-a^2-2a)$
補足 $(a+1)$ のかっこは展開しないようにしましょう。

これで平方完成は完璧だよ!
🔵2次関数のグラフの平行移動・対称移動
🔵最大・最小からの係数の決定
🔵因数分解形を利用した2次関数の決定
🔵最大・最小からの2次関数の決定
🔵2次関数のグラフと係数の符号
🔵2次関数がx軸から切り取る線分の長さ
🔵絶対不等式の解き方
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!





コメント