高校数学Ⅱで学ぶ『平行な直線と垂直な直線』について解説!
「平行な直線は傾きが同じ」
「垂直な直線は傾きの積が -1」
という条件を理解して直線に関する問題を解けるようになることが重要です!
この投稿を見れば、『平行な直線と垂直な直線』はバッチリ!

平行な直線と垂直な直線の方程式を求めよう!
直線の方程式

まずは直線の方程式の復習から!
傾き $m$,点 $(x_1,y_1)$ を通る直線の方程式は
$y-y_1=m(x-x_1)$
『傾き』と『通る点』で直線の方程式は求まる
詳しくはこれ↓

平行な直線
傾き $m$ の直線と平行な直線の傾きは $m$

平行なら傾きが等しい

問題を解いてみよう!
直線 $y=2x+1$ の傾きは $2$ なので,
求める直線の傾きは $2$ である
傾きが $2$,点 $(3,-2)$ を通る直線の方程式は
$y-(-2)=2(x-3)$
$y=2x-8$

平行な直線同士は傾きが等しい!
垂直な直線
傾き $m$ の直線と垂直な直線の傾きは $\displaystyle{-\frac{1}{m}}$
傾き $1$ の直線と傾き $-1$ の直線
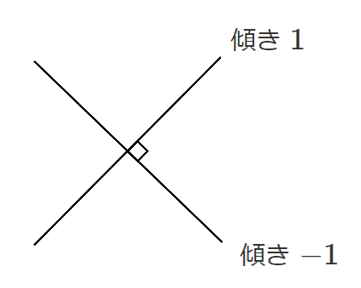
傾き $2$ の直線と傾き $\displaystyle{-\frac{1}{2}}$ の直線
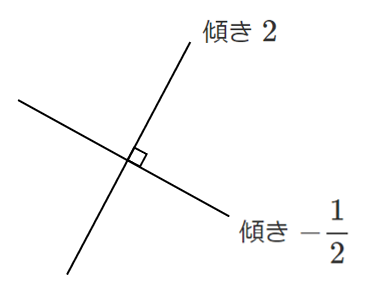
傾き $m$ の直線と傾き $\displaystyle{-\frac{1}{m}}$ の直線
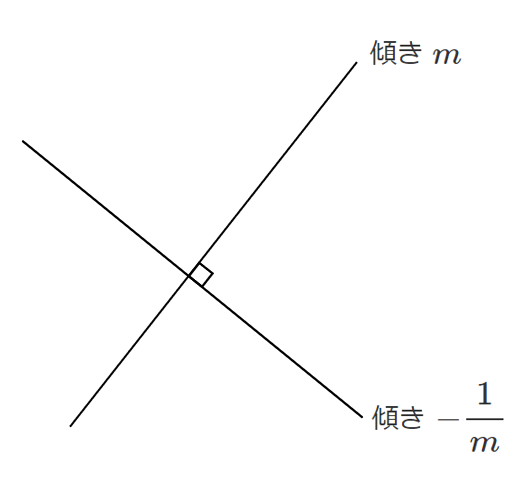
<証明>
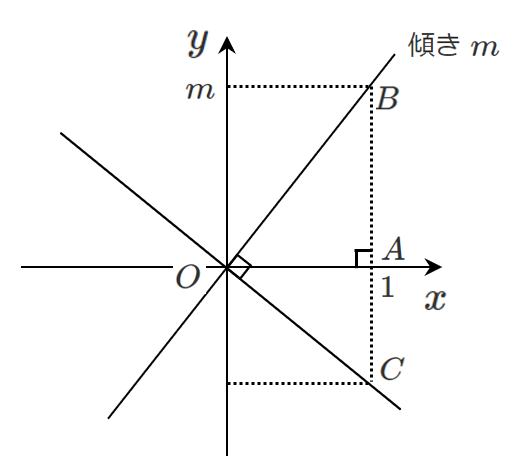
上のような図を考える
傾き $m$ の直線に垂直な直線の傾きは $\textrm{AC}$ の長さを求めることで求まる
$\triangle \textrm{OBC}$ において $\angle \textrm{OBC}$$=90^\circ -$$\angle\textrm{ OCB}$
$\triangle \textrm{OAC}$ において $\angle \textrm{AOC}$$=90^\circ -$$\angle \textrm{OCA}$
$\angle \textrm{OCB}=\angle \textrm{OCA}$ より $\angle \textrm{OBC}=\angle \textrm{AOC}$
すなわち $\angle \textrm{OBA}=\angle \textrm{AOC}$
これより $\triangle \textrm{OBA} \backsim \triangle \textrm{AOC}$
よって $\textrm{OA}:\textrm{BA}=\textrm{AC}:\textrm{OC}$
$1:m=\textrm{AC}:1$
$m\textrm{AC}=1$
$\displaystyle{\textrm{AC}=\frac{1}{m}}$
以上より,傾き $m$ と垂直な直線は
$x$ の変化量 $1$,$y$ の変化量が $\displaystyle{-\frac{1}{m}}$なので
傾きは $\displaystyle{-\frac{1}{m}}$ である

問題を解いてみよう!
直線 $y=2x+1$ の傾きは $2$ なので,
求める直線の傾きは $\displaystyle{-\frac{1}{2}}$ である
傾きが $\displaystyle{-\frac{1}{2}}$,点 $(3,-2)$ を通る直線の方程式は
$\displaystyle{y-(-2)=-\frac{1}{2}(x-3)}$
$\displaystyle{y=-\frac{1}{2}x-\frac{1}{2}}$

平行よりはややこしいけど,慣れたら大丈夫!
まとめ
● 平行な直線
平行な直線同士は傾きが等しい
傾き $m$ の直線と平行な直線の傾きは $m$
● 垂直な直線
垂直な直線同士は傾きの積が $-1$
傾き $m$ の直線と垂直な直線の傾きは $\displaystyle{-\frac{1}{m}}$
問題
$2x+3y+1=0$ を式変形すると
$\displaystyle{y=-\frac{2}{3}x-\frac{1}{3}}$ ← 傾きを求めるために式変形
直線 $2x+3y+1=0$ の傾きは $\displaystyle{-\frac{2}{3}}$
<平行な直線>
直線 $2x+3y+1=0$ と平行な直線の傾きは $\displaystyle{-\frac{2}{3}}$
求める直線は傾き $\displaystyle{-\frac{2}{3}}$,点 $(-2,3)$ を通るので
$\displaystyle{y-3=-\frac{2}{3}\{x-(-2)\}}$ より $\displaystyle{y=-\frac{2}{3}x+\frac{8}{3}}$
<垂直な直線>
直線 $2x+3y+1=0$ と垂直な直線の傾きは $\displaystyle{\frac{3}{2}}$
求める直線は傾き $\displaystyle{\frac{3}{2}}$,点 $(-2,3)$ を通るので
$\displaystyle{y-3=\frac{3}{2}\{x-(-2)\}}$ より $\displaystyle{y=\frac{3}{2}x+6}$

傾きが求まれば,『傾き』と『通る点』で直線の方程式は求まるね!
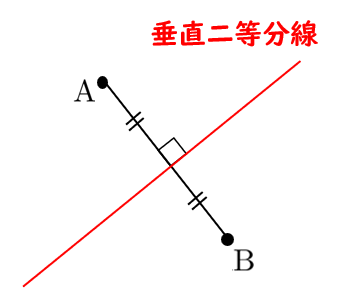
① 直線 $\textrm{AB}$ と垂直
② 線分 $\textrm{AB}$ の中点を通る
直線 $\textrm{AB}$ の傾きは $\displaystyle{\frac{-2-4}{5-1}=-\frac{3}{2}}$
よって,直線 $\textrm{AB}$ と垂直な直線の傾きは $\displaystyle{\frac{2}{3}}$
線分 $\textrm{AB}$ の中点は $\displaystyle{\left(\frac{1+5}{2},\frac{4+(-2)}{2}\right)}$ すなわち $(3,1)$
求める直線は,傾き $\displaystyle{\frac{2}{3}}$ で $(3,1)$ を通る直線であるから
$\displaystyle{y-1=\frac{2}{3}(x-3)}$ すなわち $\displaystyle{y=\frac{2}{3}x-1}$




コメント