座標平面における三角形の面積
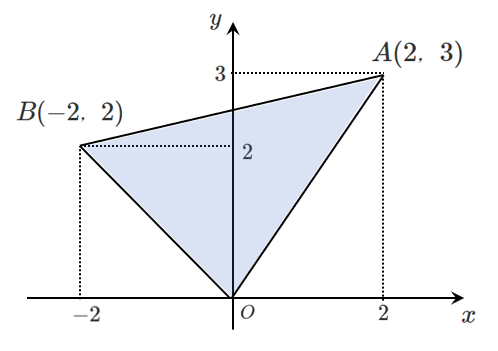

どうやって面積を求める?

直線 $AB$ の方程式を求めてから $y$ 切片を求めると面積が計算できるかな?
直線 $AB$ の傾きは
$\displaystyle{\frac{3-2}{2-(-2)}=\frac{1}{4}}$
直線 $AB$ の方程式は
$\displaystyle{y-3=\frac{1}{4}(x-2)}$
$\displaystyle{y=\frac{1}{4}x+\frac{5}{2}}$
よって,直線 $AB$ の $y$ 切片は $\displaystyle{\frac{5}{2}}$
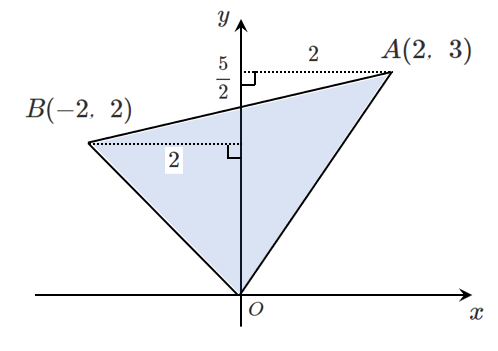
したがって,$\triangle OAB$ の面積 $S$ は
\begin{eqnarray} S &=& \frac{1}{2}\cdot\frac{5}{2}\cdot2+\frac{1}{2}\cdot\frac{5}{2}\cdot2 \\\\ &=& \frac{5}{2}+\frac{5}{2}\\\\ &=& 5 \end{eqnarray}
面積を求めることができるけど,少し時間がかかるね!
実は,簡単に求める方法があるよ!
原点 $O$,$A(a_1,a_2)$,$B(b_1,b_2)$ を頂点とする $\triangle OAB$ の面積 $S$ は
$\displaystyle{S=\frac{1}{2}|a_1b_2-a_2b_1|}$

早速使ってみよう!


便利な公式だね!
どうやったらこの式が求まるの?

求める方法はいろいろ!
今回はベクトルを用いて求めてみよう!
ベクトルを用いた三角形の面積
右図における $\triangle OAB$ の面積 $S$ は
$\displaystyle{S=\frac{1}{2}ab\sin\theta}$
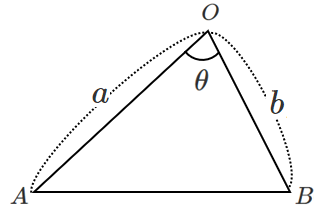
これをベクトルで表現する
$\overrightarrow{OA}=\vec{a}$,$\overrightarrow{OB}=\vec{b}$ とすると
右図における $\triangle OAB$ の面積 $S$ は
$\displaystyle{S=\frac{1}{2}|\vec{a}||\vec{b}|\sin\theta}$
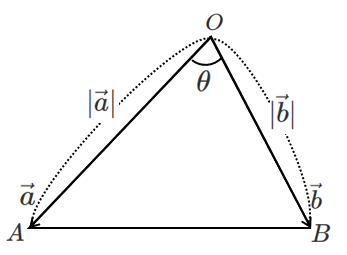
ここで,$\sin^2\theta+\cos^2\theta=1$ より
$\sin^2\theta=1-\cos^2\theta$
$0^\circ<\theta<180^\circ$ より,$\sin\theta>0$ なので
$\sin\theta=\sqrt{1-\cos^2\theta}$
$\displaystyle{\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}}$ より
\begin{eqnarray} \sin\theta &=& \sqrt{1-\frac{(\vec{a}\cdot\vec{b})^2}{|\vec{a}|^2|\vec{b}|^2}} \\\\ &=& \frac{\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}{|\vec{a}||\vec{b}|} \\\\ \end{eqnarray}これより
\begin{eqnarray} S &=& \frac{1}{2}|\vec{a}||\vec{b}|\sin\theta \\\\ &=& \frac{1}{2}|\vec{a}||\vec{b}|\frac{\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}{|\vec{a}||\vec{b}|} \\\\ &=& \frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2} \\\\ \end{eqnarray}
三角形の面積は始点がそろっている2つのベクトルの大きさと内積で求まる!
$\overrightarrow{OA}=\vec{a}$,$\overrightarrow{OB}=\vec{b}$ とすると,$\triangle OAB$ の面積 $S$ は
$\displaystyle{S=\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}$

この式を使って面積を求めてみよう!
$\triangle OAB$ において,$\overrightarrow{OA}=\vec{a}$,$\overrightarrow{OB}=\vec{b}$ とする。
$|\vec{a}|=1$,$|\vec{b}|=2$,$\displaystyle{\vec{a}\cdot\vec{b}=\frac{1}{2}}$ のとき,$\triangle OAB$ の面積 $S$ を求めよ。
成分表示を用いた三角形の面積
$\vec{a}=(a_1,a_2)$,$\vec{b}=(b_1,b_2)$ とすると
$|\vec{a}|=\sqrt{{a_1}^2+{a_2}^2}$,$|\vec{b}|=\sqrt{{b_1}^2+{b_2}^2}$
$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$
これを $\displaystyle{S=\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}$ に代入して
\begin{eqnarray} S &=& \frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2} \\\\ &=& \frac{1}{2}\sqrt{({a_1}^2+{a_2}^2)({b_1}^2+{b_2}^2)-(a_1b_1+a_2b_2)^2} \\\\ &=& \frac{1}{2}\sqrt{{a_1}^2{b_2}^2-2a_1b_1a_2b_2+{a_2}^2{b_1}^2} \\\\ &=& \frac{1}{2}\sqrt{(a_1b_2-a_2b_1)^2} \\\\ &=& \frac{1}{2}|a_1b_2-a_2b_1| \\\\ \end{eqnarray}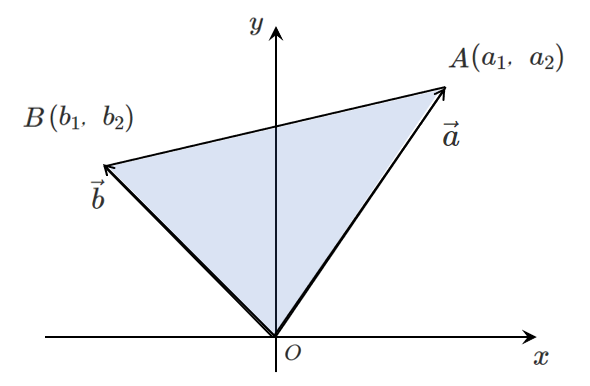
$\displaystyle{S=\frac{1}{2}|a_1b_2-a_2b_1|}$

このような計算で冒頭の式が導出できるよ!
座標平面における三角形の面積の利用
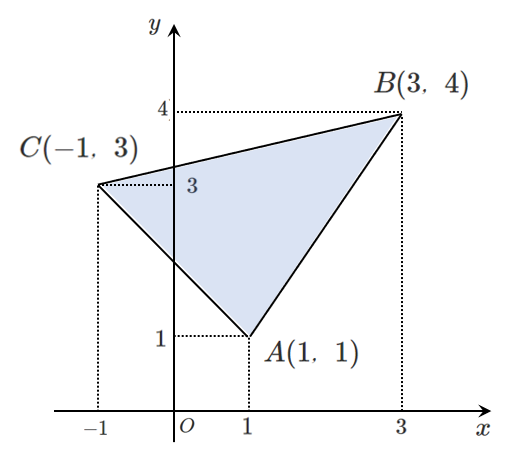

このままだと公式が使えないなあ…

そうだね!
こんなときは,どれかの頂点を原点に平行移動するように三角形を動かせばいいよ!
点 $A(1,1)$ を原点に平行移動するように
点 $B(3,4)$ と 点 $C(-1,3)$ を平行移動すると
点 $B$ は $B'(2,3)$,点 $C$ は $C'(-2,-2)$ という点に平行移動する
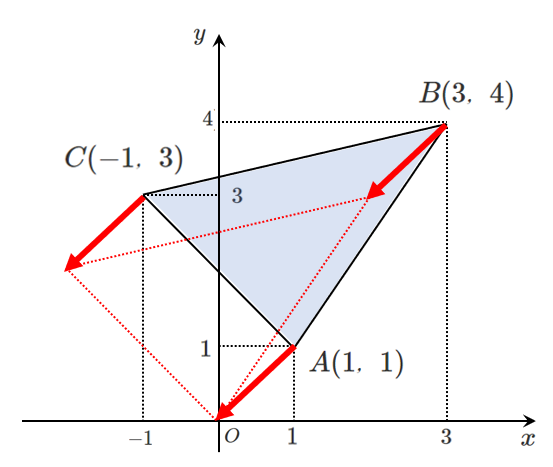
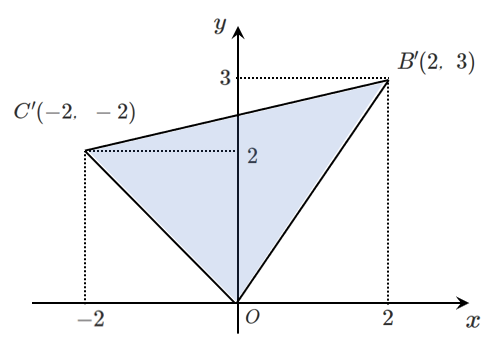
平行移動しただけなので,
$\triangle ABC$ は $triangle OB’C’$ の面積と等しい
よって
\begin{eqnarray} S &=& \frac{1}{2}|2\cdot2-3\cdot(-2)| \\\\ &=& \frac{1}{2}|10|\\\\ &=& \frac{1}{2}\cdot10\\\\ &=& 5\\\\ \end{eqnarray}
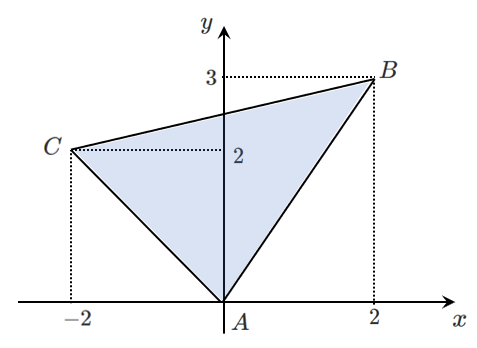
このようにベクトルで考えてもいいよ!

$\overrightarrow{AB}=(2,3)$,$\overrightarrow{AC}=(-2,2)$
以下のような図で考えることができる
まとめ
● 座標平面における三角形の面積
原点 $O$,$A(a_1,a_2)$,$B(b_1,b_2)$ を頂点とする $\triangle OAB$ の面積 $S$ は
$\displaystyle{S=\frac{1}{2}|a_1b_2-a_2b_1|}$
● ベクトルを用いた三角形の面積
$\overrightarrow{OA}=\vec{a}$,$\overrightarrow{OB}=\vec{b}$ とすると,$\triangle OAB$ の面積 $S$ は
$\displaystyle{S=\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}}$

面積を求める方法はいろいろ!
最も簡単な方法が選べるようにしよう!




コメント