接弦定理
接弦定理
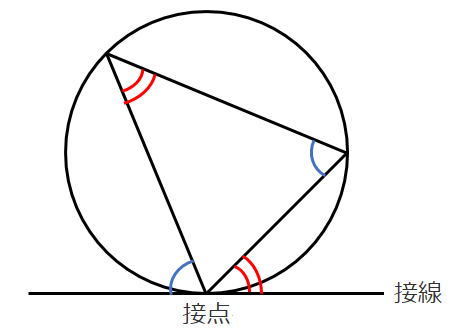
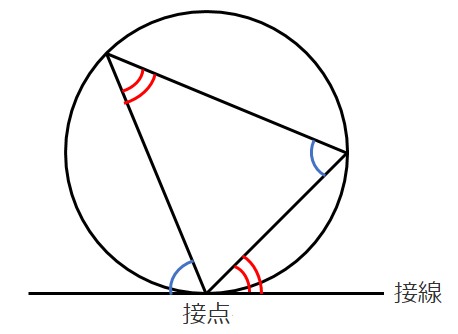
円の接線とその接点を通る弦の作る角は,その角の内部にある弧に対する円周角に等しい

文章では分かりにくいので,図で覚えておこう!
証明

なぜ接弦定理は成り立つのかな?

接弦定理を証明してみよう!
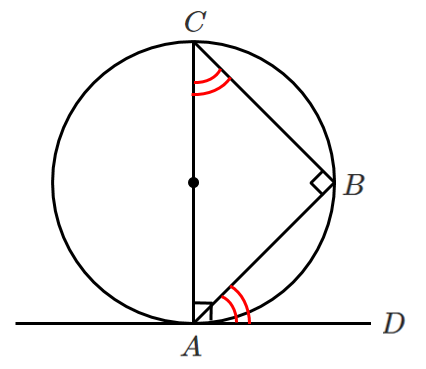
上図で考えると
$\angle ACB+\angle BAC=90°$
$\angle BAD+\angle BAC=90°$
よって $\angle ACB=\angle BAD$
ここで,下図のように点 $P$ をとると
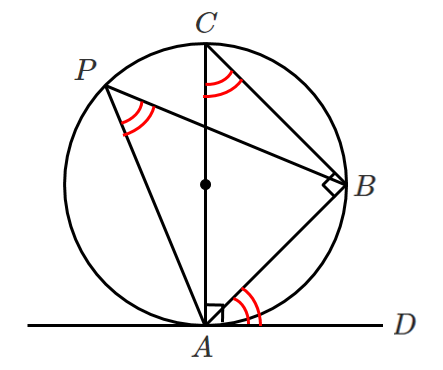
円周角の定理より $\angle ACB=\angle APB$
したがって $\angle BAD=\angle APB$
接弦定理による相似な図形

接弦定理を使って相似な図形を見つけてみよう!
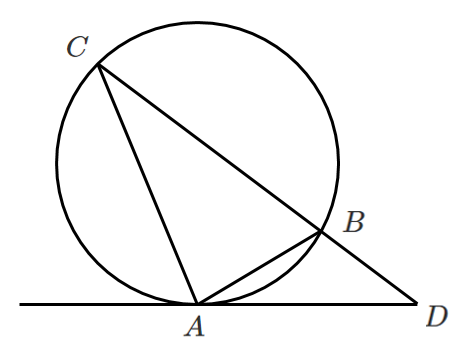

接弦定理を使うと
$\angle BCA=\angle BAD$
だよね!
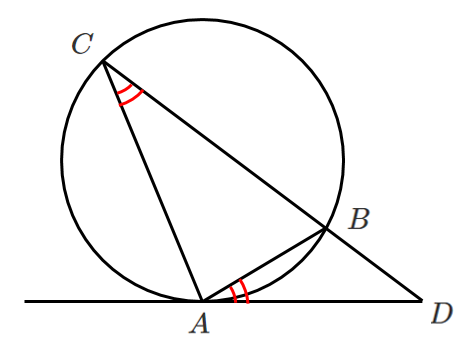

あとは $\angle D$ を共通な角と考えたら
$\triangle ABD\backsim\triangle CAD$
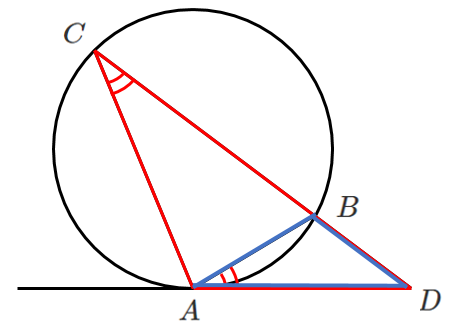
$\triangle ABD$$\backsim$$\triangle CAD$

このような図が出題されたら,相似を見つけられるようにしよう!
まとめ
● 接弦定理
問題
以下の図において,$α$ と $β$ を求めよ。
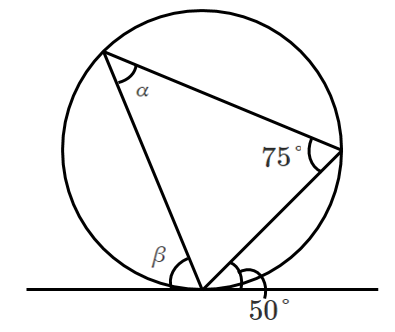
接弦定理より
$α=50°$,$β=75°$

円の接線の問題が出たら,接弦定理を思い出そう!




コメント