高校数学Ⅱで習う『整式の除法』についてわかりやすく解説しました!
筆算を用いた整式の除法や「(割られる式)=(割る式)×(商)+(余り)」を利用する問題を扱っています!
整式の基本なので、確実にマスターしましょう!
整式の除法の筆算
小学校で習った『数の割り算の筆算』と同様に、整式の割り算でも筆算が使える。
例えば、$139÷3$ の筆算は
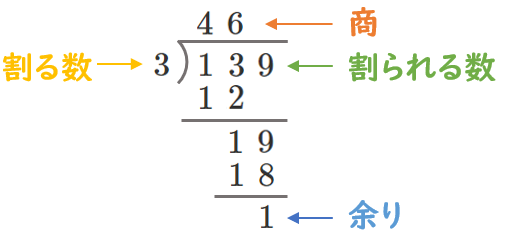
整式の割り算も同様に、割られる式 $A$、割る式 $B$、商 $Q$、余り $R$ とすると、以下のような筆算が作れる。
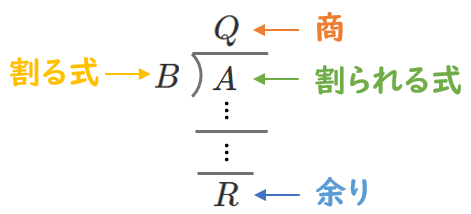
ただし、(3)は$x$ についての整式と考えよ。
(1) $A=2x^3+7x^2+5$,$B=x+3$
(2) $A=2x^3+4x^2-x+3$,$B=2x^2-2$
(3) $A=x^4+x^2y^2+y^4$,$B=x^2+xy+y^2$
(1) $A=2x^3+7x^2+5$,$B=x+3$
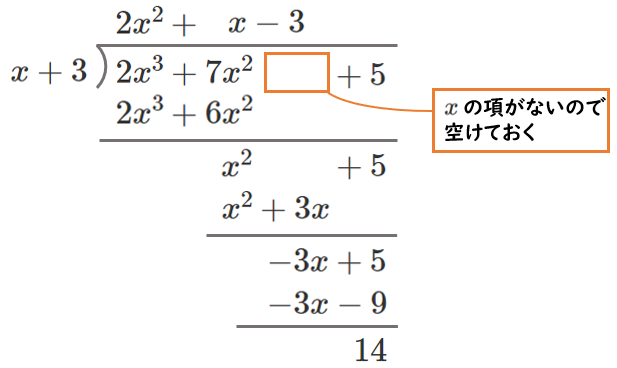
商 $Q=2x^2+x-3$、余り $R=14$
(2) $A=2x^3+4x^2-x+3$,$B=2x^2-2$
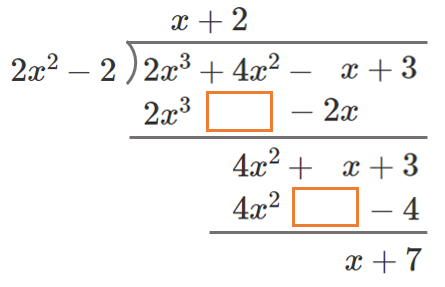
商 $Q=x+2$、余り $R=x+7$
(3) $A=x^4+x^2y^2+y^4$,$B=x^2+xy+y^2$
2文字以上の整式の除法は、1つの文字(今回は $x$)に着目する
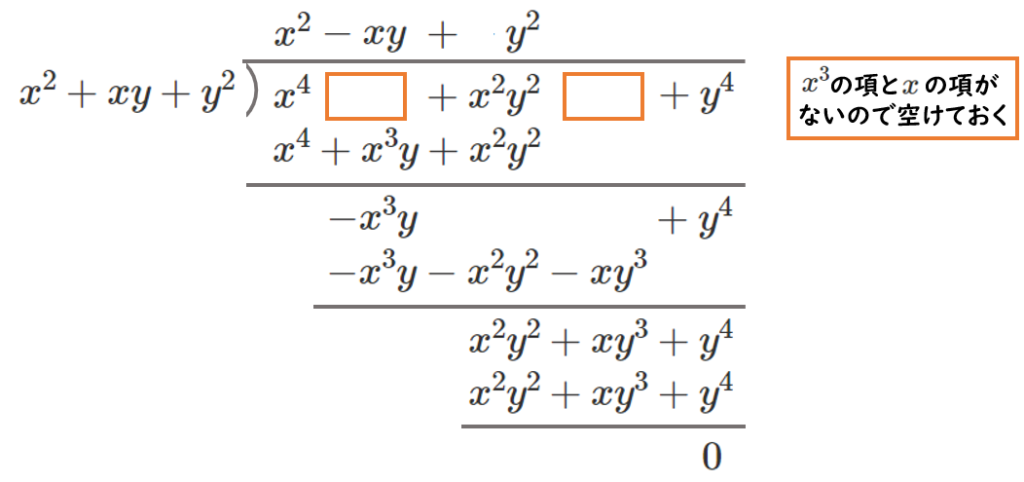
商 $Q=x^2-xy+y^2$、余り $R=0$
(割られる式)=(割る式)×(商)+(余り)
$100$ を $6$ で割ったときの商は $16$、余りは $4$ である。
これを式で表すと $100=6\times16+4$ (割られる数)=(割る数)×(商)+(余り)
もちろん (余り)$<$(割る数) が成り立つ。
なぜなら「りんご10個を3人で分けたら(割る数3)、4個余りました(余り4)」はおかしいからです。
整式でも同様の式を作ることができます。
整式 $A$ を整式 $B$ で割ったときの商を $Q$、余りを $R$ とすると
$A=BQ+R$ (ただし、余り $R$ の次数$<$割る式 $B$ の次数)
という関係が成り立つ。
余り $R$ の次数$<$割る式 $B$ の次数 について

この筆算を見て、何か気付くかな?
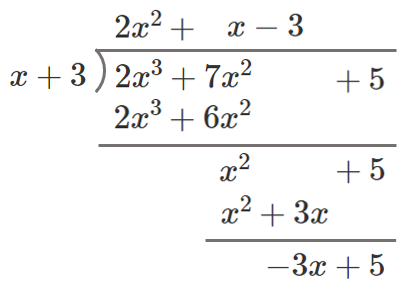

まだ割れそうだよ!

整式の割り算は、余りの次数が商の次数よりも小さくなるまで割るはずです。
つまり、【余り $R$ の次数$<$割る式 $B$ の次数】が成り立ちます。
(2) 整式 $6x^3+x^2-x-15$ を $x$ の整式 $B$ で割ると、商が $3x^2+5x+7$、余りが $6$ である。このとき、整式 $B$ を求めよ。
(1) $x$ の整式 $A$ を $x^2+2x+1$ で割ると、商が $x^2+3x-2$、余りが $2x-3$ となった。このとき、整式 $A$ を求めよ。
$A=($$x^2+2x+1$$)($$x^2+3x-2$$)+$$2x-3$ より
(割られる式)=(割る式)×(商)+(余り)
(2) 整式 $6x^3+x^2-x-15$ を $x$ の整式 $B$ で割ると、商が $3x^2+5x+7$、余りが $6$ である。このとき、整式 $B$ を求めよ。
$6x^3+x^2-x-15=$$B$$($$3x^2+5x+7$$)+$$6$ より
(割られる式)=(割る式)×(商)+(余り)
$6x^3+x^2-x-21=B(3x^2+5x+7)$
$B=(6x^3+x^2-x-21)÷(3x^2+5x+7)$
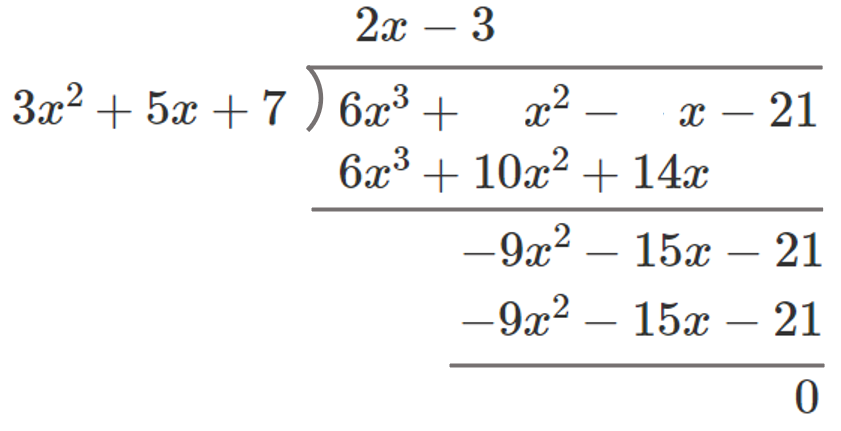
よって $B=2x-3$ (答)




コメント