多くの高校生が初見で解けない『文字係数の方程式』について解説しました!
『文字係数の方程式』は場合分けが必要な問題があります。
知っているのと知らないのとでは大きな差がつく問題です。
この投稿を見れば、『文字係数の方程式』の解法を理解することができます!
問題
(1) $x^2+(a-2)x-2a=0$
(2) $a^2x-a=2ax$
(3) $ax^2-x-a=0$
(1) $x^2+(a-2)x-2a=0$
$(x-2)(x+a)=0$
$x=2,-a$
(2) $a^2x-a=2ax$ より $a(a-2)x=a$
(ア) $a=0$ のとき,この方程式は $0\cdot x=0$
よって,すべての $x$ で成り立つから,解はすべての実数
(イ) $a=2$ のとき,この方程式は $0\cdot x=2$
この式は成り立たないから,解はない
(ウ) $a≠0,2$ のとき $\displaystyle{x=\frac{1}{a-2}}$
(ア)~(ウ) より
(3) $ax^2-x-a=0$
(ア) $a=0$ のとき,この方程式は $-x=0$
これを解くと $x=0$
(イ) $a≠0$ のとき,解の公式より
$\displaystyle{x=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot a\cdot(-a)}}{2a}=\frac{1\pm\sqrt{4a^2+1}}{2a}}$
$4a^2+1>0$ より,これは解として適する
(ア)~(イ) より
文字係数の2次方程式|たすき掛け
(1) $x^2+(a-2)x-2a=0$
2次方程式を解くときに、最初に考えることは「因数分解できないか」です。
因数分解ができないようならば、解を公式を使います。
今回の問題は因数分解できるので、たすき掛けをして因数分解をします。
$x^2+(a-2)x-2a=0$
$(x-2)(x+a)=0$
$x=2,-a$
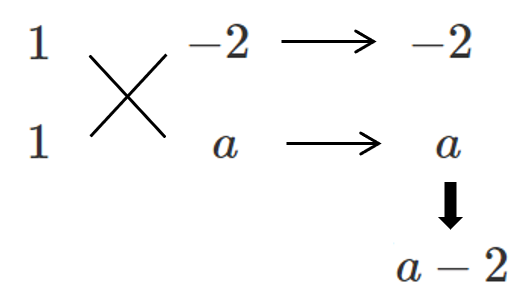
文字係数の1次方程式|場合分け
(2) $a^2x-a=2ax$
まずは式を整理します
$a^2x-a=2ax$
$a^2x-2ax=a$
$(a^2-2a)x=a$
$a(a-2)x=a$
次に両辺を $a(a-2)$ で割りたいところですが、要注意です!
文字で割るときに注意しなければならないのが、
その文字が $0$ である場合と $0$ でない場合に分けて考えなければならないこと!
なぜ場合分けが必要なのかというと、$0$ で割ることはできないからです。0で割れない理由
今回は両辺を $a(a-2)$ で割りたいので、
$a(a-2)=0$ のとき
すなわち (ア) $a=0$ のとき または (イ) $a=2$ のとき
$a(a-2)≠0$ のとき
すなわち (ウ) $a≠0$,$2$ のとき
に分けて解答を作る必要があります。
$a(a-2)x=a$ より
(ア) $a=0$ のとき,この方程式は $0\cdot x=0$
すべての $x$ で成り立つ($x$ に何が代入されても等式が成り立つ)から,解はすべての実数
(イ) $a=2$ のとき,この方程式は $0\cdot x=2$
この式は成り立たない($x$ に何を代入しても左辺は $0$)から,解はない
(ウ) $a≠0,2$ のとき,両辺を $a(a-2)$ で割って【$a(a-2)≠0$ なので割れる】
$\displaystyle{x=\frac{a}{a(a-2)}=\frac{1}{a-2}}$
(ア)~(ウ) より
\begin{align} & \left\{ \begin{array}{lll} a=0 のとき すべての実数 \\ a=2 のとき 解なし \\ a≠0,2 のとき x=\frac{1}{a-2} \end{array} \right. \end{align}文字係数の2次方程式|場合分け
(3) $ax^2-x-a=0$
因数分解できなさそうなので、解の公式を使うのかと思いきや…
この方程式は
$x^2$ の係数が $0$ のとき、1次方程式
$x^2$ の係数が $0$ でないとき、2次方程式
という2パターンに分けられます。
もちろん、解き方も異なるので場合分けが必要です。
$ax^2-x-a=0$
(ア) $a=0$ のとき,この方程式は $-x=0$(1次方程式)
これを解くと $x=0$
(イ) $a≠0$ のとき,この方程式は $ax^2-x-a=0$(2次方程式)
解の公式より $\displaystyle{x=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot a\cdot(-a)}}{2a}=\frac{1\pm\sqrt{4a^2+1}}{2a}}$
$4a^2+1>0$ より,これは解として適する(√の中が負の数でないことを確認)
(ア)~(イ) より
\begin{align} & \left\{ \begin{array}{ll} a=0 のとき x=0 \\ a≠0 のとき x=\frac{1\pm\sqrt{4a^2+1}}{2a} \end{array} \right. \end{align}まとめ
補足:0で割れない理由
割り算とかけ算の関係から、$0$ で割れない理由を考えてみましょう。
割り算 $6÷3=2$ は かけ算 $2\times3=6$ と変形できます。
つまり、$a÷b$ の答えは、$□\times b=a$ を満たす□のこと。
よって、$6÷0$ の答えは、$□\times 0=6$ を満たす□ですが、$□\times 0=6$ を満たすような□に入る数は存在しません。
なぜなら、□にどのような数が入ろうとも、左辺は $0$ になり、右辺と異なるからです。
これより、$6÷0$ の答えが存在しないことがわかります。
今回は、$6$ を $0$ で割りましたが、他の数も同様に $0$ で割っても答えが存在しないので、$0$ で割ることができません。
🔴軸に定数を含む2次関数の最大・最小の場合分け
🔴定義域の片端に定数を含む2次関数の最大・最小の場合分け
🔴定義域の両端に定数を含む2次関数の最大・最小の場合分け
🔵因数分解形を利用した2次関数の決定
🔵2次関数のグラフと係数の符号
🔴文字係数の2次不等式
🔴異なる2つの正の解・負の解・異符号
🔴異なる2つの○より大きい・小さい解
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント