2次不等式の応用編『文字係数の2次不等式』についてわかりやすく解説しました!
一見難しそうに見えますが、因数分解と2次不等式の基本(2次関数のグラフを用いて解くこと)がわかれば理解することができます!
2次不等式の基本的な問題が解ける人はチャレンジしてみましょう!
問題
(1) $x^2-(2a+1)x+a^2+a>0$
(2) $x^2-(a+1)x+a<0$
(3) $ax^2-ax-2a>0$
(1) $x^2-(2a+1)x+a^2+a>0$
式変形して $x^2-(2a+1)x+a(a+1)>0$
左辺を因数分解すると $(x-a)\{x-(a+1)\}>0$
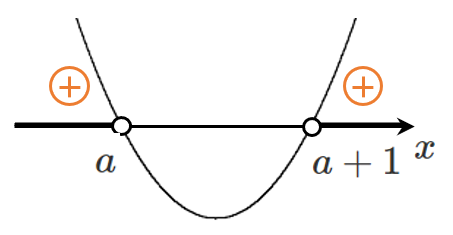
$a<a+1$ より $x<a$,$a+1<x$
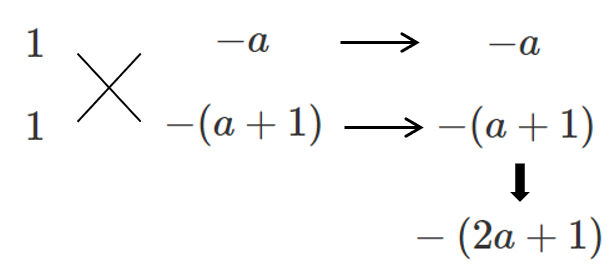
(2) $x^2-(a+1)x+a<0$
左辺を因数分解すると $(x-a)(x-1)<0$ ←$a$ と $1$ の大小関係で場合分け
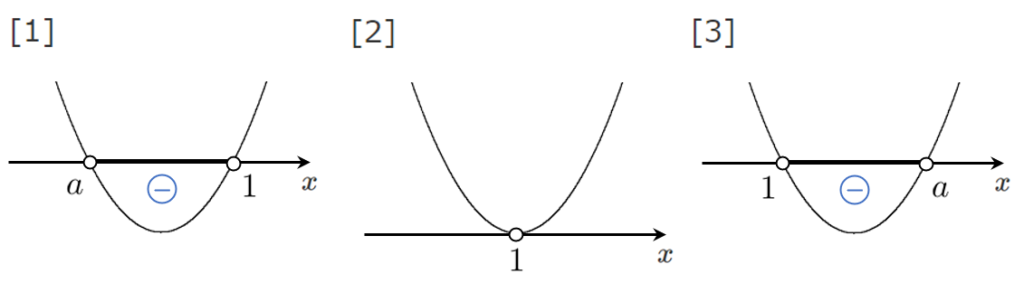
[1] $a<1$ のとき $a<x<1$
[2] $a=1$ のとき $(x-1)^2<0$ より 解はない
[3] $1<a$ のとき $1<x<a$
(3) $ax^2-ax-2a>0$
左辺を因数分解すると $a(x^2-x-2)>0$
$a(x+1)(x-2)>0$
[1] $a>0$ のとき $x<-1$,$2<x$
[2] $a=0$ のとき $0>0$ より 解はない
[3] $a<0$ のとき $-1<x<2$
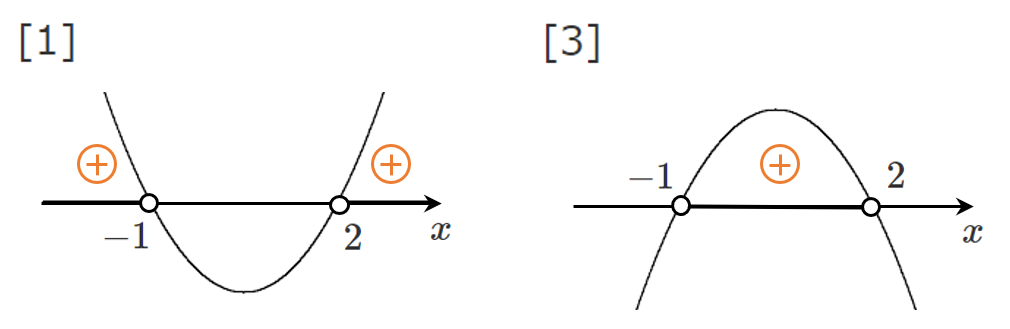
文字係数の2次不等式|文字の大小を判断
(1) $x^2-(2a+1)x+a^2+a>0$
(1)
定数項を因数分解して $x^2-(2a+1)x+a(a+1)>0$
左辺を因数分解すると(たすき掛け)
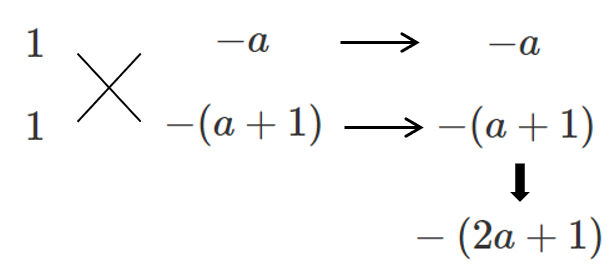
$(x-a)\{x-(a+1)\}>0$
$a$ と $a+1$ の大小を比較すると $a<a+1$
($a$ に $1$ を足したのが $a+1$ なので)

$x<a$,$a+1<x$
文字係数の2次不等式|文字の大小で場合分け
(2) $x^2-(a+1)x+a<0$
(2)
左辺を因数分解すると $(x-a)(x-1)<0$
$a$ と $1$ の大小関係で場合分け
[1] $a$ が $1$ より小さいとき($a<1$)
[2] $a$ が $1$ と等しいとき ($a=1$)
[3] $a$ が $1$ より大きいとき($1>a$)
[1] $a<1$ のとき $a<x<1$
[2] $a=1$ のとき $(x-1)^2<0$ より 解はない
[3] $1<a$ のとき $1<x<a$

※$a$ と $1$ の大小関係で図が異なる
文字係数の2次不等式|文字の正負で場合分け
(3) $ax^2-ax-2a>0$
(3)
左辺を因数分解すると $a(x^2-x-2)>0$
$a(x+1)(x-2)>0$
$a$ の符号で場合分け
[1] $a$ が正のとき(下に凸の2次関数)
[2] $a$ が $0$ のとき(左辺が $0$)
[3] $a$ が負のとき(上に凸の2次関数)
[1] $a>0$ のとき $x<-1$,$2<x$
[2] $a=0$ のとき $0>0$ より 解はない
[3] $a<0$ のとき $-1<x<2$
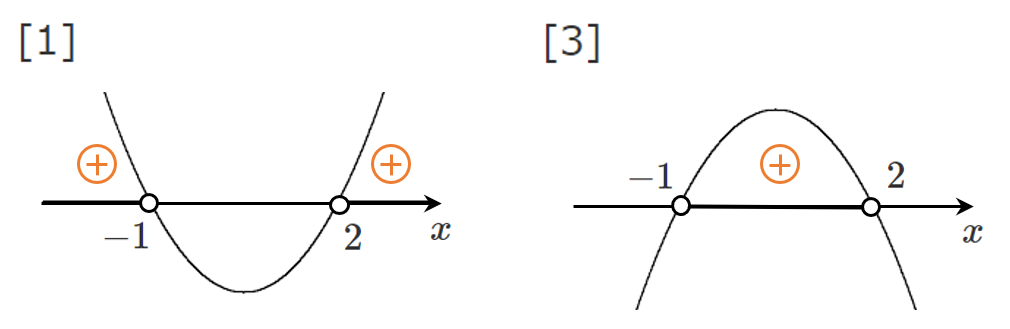




コメント