条件の否定を答えることができる?
意外と答えられない人が多いですが,
やり方がわかればとても簡単!
ポイントは,条件の否定のパターンをきちんと把握しておくこと!
この投稿を見れば,条件の否定は完璧です!
条件の否定
条件 $p$ に対して 「$p$ でない」を $p$ の否定 という

集合 $A$ における「補集合 $\overline{A}$」と似ているね!
補集合について↓
$x$ を実数とする。次の条件の否定を答えよ。
(1) $x$ は有理数である
(2) $x>0$
(1) 「$x$ は有理数である」の否定
$x$ は有理数でない
すなわち $x$ は無理数である

実数は必ず「有理数」か「無理数」のどちらかに分類されるので、
「有理数でない」ということは「無理数である」ということ!
有理数と無理数の復習はこれ↓

(2) 「$x>0$」の否定
$x>0$ でない
すなわち $x≦0$
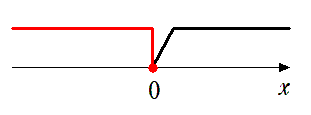

$=$ の付け忘れに注意しないとね!
「かつ」「または」の否定

「ド・モルガンの法則」覚えてる?

$\overline{A∩B}=\overline{A}∪\overline{B}$
$\overline{A∪B}=\overline{A}∩\overline{B}$
だったよね!

よく覚えてたね!
これを使うと「かつ」「または」の否定も簡単だよ!
ド・モルガンの法則はこれ↓

『 $pかつq$ 』 の否定は 『 $\overline{p}または\overline{q}$ 』
『 $pまたはq$ 』 の否定は 『 $\overline{p}かつ\overline{q}$ 』

これを使って問題を解いてみよう!
$a,b$ を実数とする。次の条件の否定を答えよ。
(1) $a$ は偶数 かつ $b$ は偶数
(2) $a=0$ または $b=0$
(1) 「 $a$ は偶数 かつ $b$ は偶数 」の否定
$a$ は奇数 または $b$ は奇数
(2) 「 $a=0$ または $b=0$ 」の否定
$a≠0$ かつ $b≠0$
「少なくとも一方が」「ともに」の否定

「少なくとも一方が」「ともに」の否定ってどうなるのかな?
$m,n$ を自然数とする。次の条件の否定を答えよ。
(1) $m,n$ の少なくとも一方が奇数
(2) $m,n$ がともに奇数
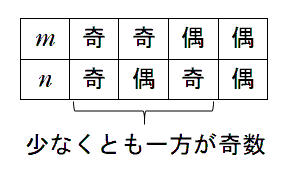
(1) 「 $m,n$ の少なくとも一方が奇数 」の否定
$m,n$ の少なくとも一方が奇数は下の3つの場合がある
その否定なので $m,n$ がともに偶数
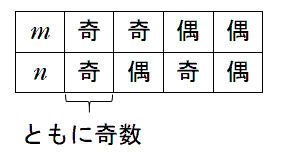
(2) 「 $m,n$ がともに奇数 」の否定
$m,n$ がともに奇数以外は3つの場合がある
よって $m,n$ の少なくとも一方が偶数
「 $m,n$ の少なくとも一方が奇数 」の否定は「 $m,n$ がともに偶数 」
「 $m,n$ のともに奇数 」の否定は「 $m,n$ の少なくとも一方が偶数 」
『 〇,〇の少なくとも一方が $p$ 』の否定は『 〇,〇がともに $\overline{p}$ 』
『 〇,〇がともに $p$ 』の否定は『 〇,〇の少なくとも一方が $\overline{p}$ 』
まとめ
● 「かつ」「または」の否定
『 $pかつq$ 』 の否定は 『 $\overline{p}または\overline{q}$ 』
『 $pまたはq$ 』 の否定は 『 $\overline{p}かつ\overline{q}$ 』
● 「少なくとも一方が」「ともに」の否定
『 〇,〇の少なくとも一方が $p$ 』 の否定は 『 〇,〇がともに $\overline{p}$ 』
『 〇,〇がともに $p$ 』 の否定は 『 〇,〇の少なくとも一方が $\overline{p}$ 』
問題
$a,b$ を実数とする。次の条件の否定を答えよ。
(1) $0<$$a≦1$
(2) $a<0$ または $b≧0$
(3) $a=0$ かつ $b=0$
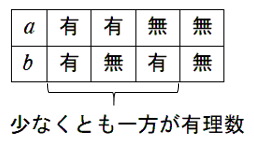
(4) $a,b$ のうち少なくとも一方が有理数である
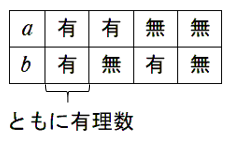
(5) $a,b$ ともに有理数である
解答
(1) 「 $0<$$a≦1$ 」の否定
$a≦0,1<a$

(2) 「 $a<0$ または $b≧0$ 」の否定
$a≧0$ かつ $b<0$
(3) 「 $a=0$ かつ $b=0$ 」の否定
$a≠0$ または $b≠0$
(4) 「 $a,b$ のうち少なくとも一方が有理数である 」の否定
$a,b$ がともに無理数である
(5) 「 $a,b$ ともに有理数である 」の否定
$a,b$ の少なくとも一方が無理数である
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント