
よく出題されるけど,理解できていない高校生が多いテーマ!
きちんとおさえておこう!
極値をもつための条件

今回学ぶのはこれ!
$D>0$ $\iff$ 関数 $f(x)$ は極値をもつ

急に判別式 $D$ が出てきた…
全く理解できない…

これが理解できれば,極値に対する理解も深まる!
ひとつひとつ理解していけば必ず分かるよ!
極値とは
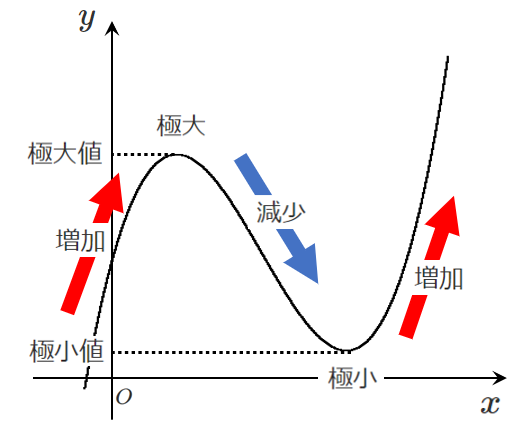
極大 … 増加から減少に切りかわるところ
極小 … 減少から増加に切りかわるところ
極大における $y$ の値を極大値
極小における $y$ の値を極小値
極大値と極小値をまとめて 極値
逆に,増減が入れかわらないような
常に増加する または 常に減少する
関数は極値をもたない
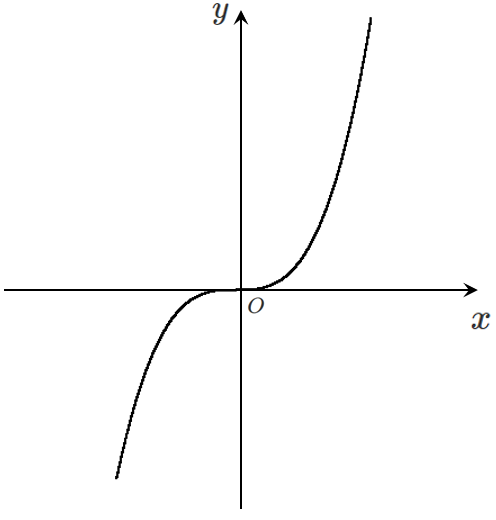
常に増加するので,極値をもたない
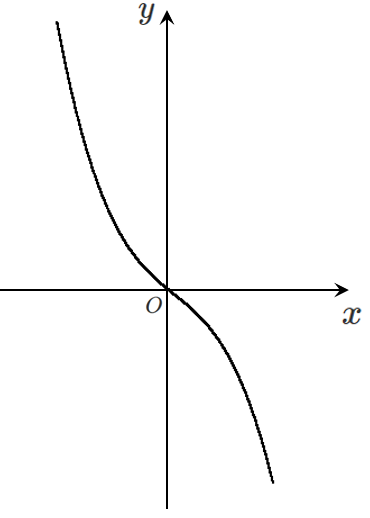
常に減少するので,極値をもたない

極値をもつ,もたないは,増減が入れかわるかどうかがポイントだね!
関数の増減と $f'(x)$ の関係

増減が入れかわるかどうかで,極値をもつ,もたないが決まる!
ここで,関数の増減が調べられる,導関数 $f'(x)$ について復習しよう!
$f'(x)<0$ となる $x$ の値の範囲では $f(x)$ は減少する
「関数の増減と $f'(x)$ の関係」詳しくはこれ↓


$f'(x)$ の符号によって,関数 $f(x)$ の増減が決まる!
つまり,増減が入れかわるかどうかは,$f'(x)$ の符号が入れかわるかどうかで調べられる!
$f'(x)$ の符号が入れかわらないとき,関数 $f(x)$ の増減が入れかわらないので極値をもたない
$f'(x)$ の比較

極値をもつときともたないときの $f'(x)$ について,具体的に比較してみよう!
極値をもつ関数
導関数 $f'(x)$ を求めると
$f'(x)=3x^2-6x=3x(x-2)$
$f'(x)=0$ を求めると
$3x(x-2)=0$
$x=0,2$
$f'(x)$ のグラフをかくと
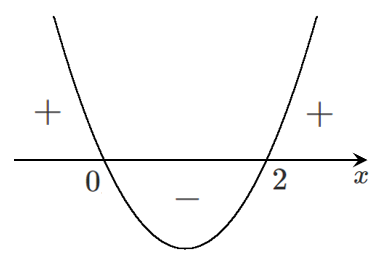
$f'(x)$ の符号が入れかわるので増減が入れかわる
関数 $f(x)=x^3-3x^2$ は極値をもつ
極値をもたない関数
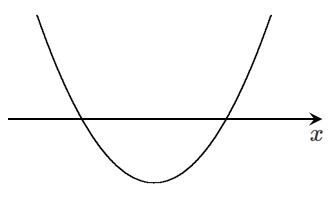
導関数 $f'(x)$ を求めると
$f'(x)=3x^2$
$f'(x)=0$ を求めると
$3x^2=0$
$x=0$
$f'(x)$ のグラフをかくと
$f'(x)$ の符号が入れかわらないので常に増加する
関数 $f(x)=x^3$ は極値をもたない
導関数 $f'(x)$ を求めると
$f'(x)=3x^2+1$
$f'(x)=0$ を求めると
$3x^2=-1$
この方程式は実数解をもたない
$f'(x)$ のグラフをかくと
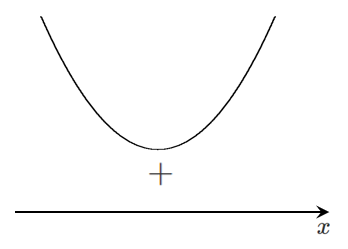
$f'(x)$ の符号が入れかわらないので常に増加する
関数 $f(x)=x^3+x$ は極値をもたない
極値をもつための $f'(x)$ のグラフの条件

3つの関数の $f'(x)$ について考えてみたけど,違いに気づいた?

$x$ 軸との共有点の個数が違うみたいだね!
① $f'(x)=3x(x-2)$
共有点2個
② $f'(x)=3x^2$
共有点1個

③ $f'(x)=3x^2+1$
共有点0個


その通り!
$x$ 軸との共有点が2個のときだけ,$f'(x)$ の符号が入れかわることがわかるね!

$f'(x)$ と $x$ 軸との共有点が2個のときは極値をもつということがいえそう!

2次関数のグラフと $x$ 軸の共有点の個数はどうやって調べられる?

判別式 $D$ で調べられる!
数学Ⅰで習ったね!
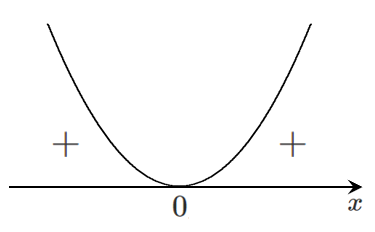
2次関数 $y=ax^2+bx+c$ に $y=0$ を代入した
2次方程式 $ax^2+bx+c=0$ の判別式を $D=b^2-4ac$ とすると
2点で交わる
$D>0$
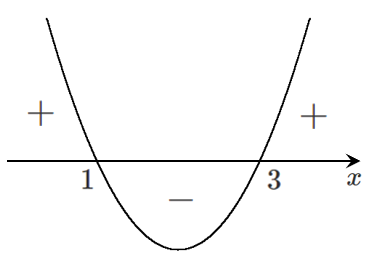
1点で交わる
$D=0$
交わらない
$D<0$
$f'(x)$ と $x$ 軸の共有点が2個のとき,関数 $f(x)$ は極値をもつ
すなわち
$f'(x)=0$ の判別式を $D$ とするとき,
$D>0$ $\iff$ 関数 $f(x)$ は極値をもつ
$D>0$ $\iff$ 関数 $f(x)$ は極値をもつ
問題
関数 $f(x)=x^3-ax^2+3x$ を微分すると
$f'(x)=3x^2-2ax+3$
$3x^2-2ax+3=0$ の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=a^2-9}$
$f(x)$ が極値をもつとき,$D>0$ なので
$a^2-9>0$
$(a+3)(a-3)>0$
$a<-3,3<a$

分かっていれば,判別式を使うだけで解けるね!
まとめ
● 極値をもつための条件
$f'(x)=0$ の判別式を $D$ とすると
$D>0$ $\iff$ 関数 $f(x)$ は極値をもつ

極値に関する理解も深まったね!




コメント