数学Ⅰ「図形と計量」分野で登場機会が多い『正弦定理』
簡単に思われがちな定理ですが,使う場面を整理していないと痛い目をみます!
また,計算ミスが非常に多いことも特徴です!
この投稿を見れば,『正弦定理』の使い方が整理でき,計算ミスも確実に減らせます!
△ABCについて
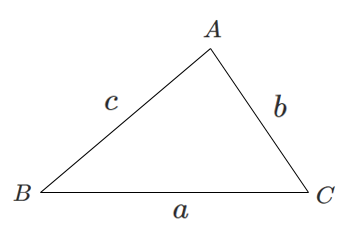
$\triangle ABC$ の各頂点 $A$,$B$,$C$ の向かい合う辺の長さをそれぞれ $a$,$b$,$c$ とする
正弦定理
$\triangle ABC$ の外接円の半径を $R$ とすると
$ \displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

この式のまま使うことはないので注意しよう!
$\sin$ の値に自信がない人はこれ↓

正弦定理の使い方①
$\displaystyle\frac{a}{\sin A}=2R$
簡単に表すと
$$\displaystyle\frac{●}{\sin■}=2R$$
1組の向かい合う辺と角と外接円の半径で式を作る
三角形の外接円の半径を求める
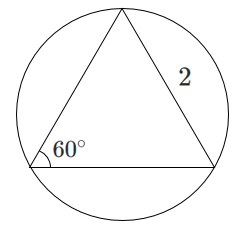
三角形の外接円の半径を用いて,辺や角($\sin$ の値)を求める
正弦定理より
$$\displaystyle\frac{x}{\sin60^\circ}=2\sqrt{3}$$
$$x=2\sqrt{3}\sin60^\circ$$
$$\displaystyle x=2\sqrt{3}×\frac{\sqrt{3}}{2}$$
$$x=3$$

問題文に「外接円の半径」があったら,正弦定理を思い出すことが大切だね!
正弦定理の使い方②
$\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}$
2組の向かい合う辺と角($\sin$ の値)のうち3つが与えられているなら,残りの辺または角($\sin$ の値)が求まる
簡単に表すと
$$\displaystyle\frac{●}{\sin ■}=\frac{○}{\sin □}$$
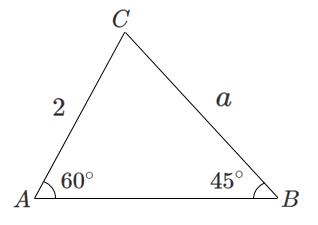
2組の向かい合う辺と角で式を作る
辺の長さを求める
(※)について
$$\displaystyle\frac{a}{b}=\frac{c}{d}$$
両辺に $bd$ をかけると $ad=bc$
正弦定理の計算をするときは斜めにかける
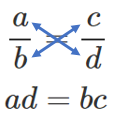
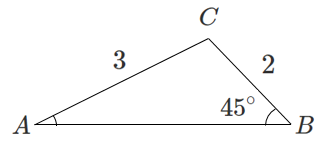
角($\sin$ の値)を求める
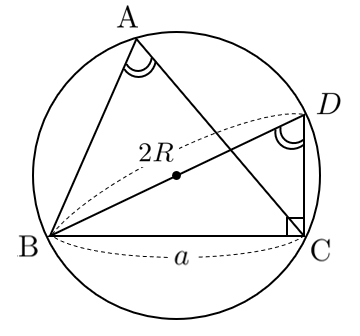
正弦定理の証明
円周角の定理と直径を斜辺とする直角三角形を利用して、
$\displaystyle{\frac{a}{\sin A}=2R}$ を $\angle\textrm{A}$ が鋭角・直角・鈍角によって分けて考える。
(ア)$\textrm{A}<90^\circ$ のとき
円周角の定理より $\sin A=\sin D$ … ①
$\triangle\textrm{BCD}$ について $\displaystyle{\sin D=\frac{a}{2R}}$ … ②
①、②より $\displaystyle{\sin A=\frac{a}{2R}}$
すなわち $\displaystyle{\frac{a}{\sin A}=2R}$
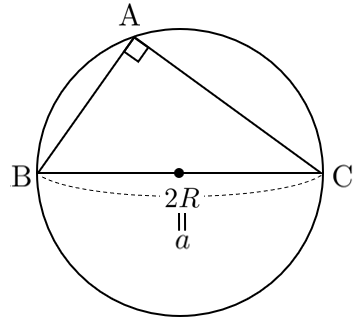
(イ)$\textrm{A}=90^\circ$ のとき
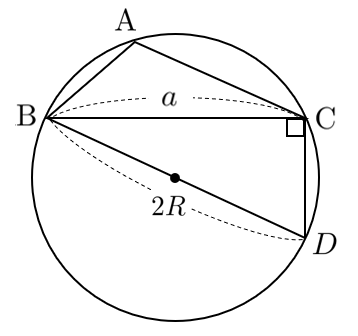
(ウ)$\textrm{A}>90^\circ$ のとき
円に内接する四角形の性質より $A=180^\circ-D$
よって $\sin A=\sin(180^\circ-D)=\sin D$ … ①
また $\displaystyle{\sin D=\frac{a}{2R}}$ … ②
①、②より $\displaystyle{\sin A=\frac{a}{2R}}$
すなわち $\displaystyle{\frac{a}{\sin A}=2R}$
まとめ
● 正弦定理
$\triangle ABC$ の外接円の半径を $R$ とすると
$\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
● 正弦定理の使い方①
$\displaystyle\frac{●}{\sin■}=2R$

- 三角形の外接円の半径を求める
- 三角形の外接円の半径を用いて,辺の長さや角の大きさ($\sin$ の値)を求める
● 正弦定理の使い方②
$\displaystyle\frac{●}{\sin ■}=\frac{○}{\sin □}$

- 2組の向かい合う辺と角($\sin$ の値)のうち3つが与えられているなら,残りの辺または角($\sin$ の値)が求まる

・「外接円の半径」が問題文にある
・2組の向かい合う辺と角で式が作れる
ときは正弦定理!




コメント