高校数学Ⅰの2次関数の応用問題の1つである
2次方程式が異なる2つの正の解をもつ
2次方程式が異なる2つの負の解をもつ
2次方程式が符号の異なる2つの解をもつ
という問題をわかりやすく解説しました!
ポイントは、『判別式・軸の位置・端点の $y$ 座標』に着目すること!
2次関数の図をかいて、それぞれの条件を整理すれば必ず解けます!
問題
(2) 2次方程式 $x^2-2ax-a+2=0$ が異なる2つの負の解をもつときの $a$ の値の範囲を求めよ。
(3) 2次方程式 $x^2-2ax-a+2=0$ が符号の異なる2つの解をもつときの $a$ の値の範囲を求めよ。
(1)
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異なる2つの正の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の正の部分と異なる2つの共有点をもつことである
よって,次の [1]~[3] がすべて成り立つ
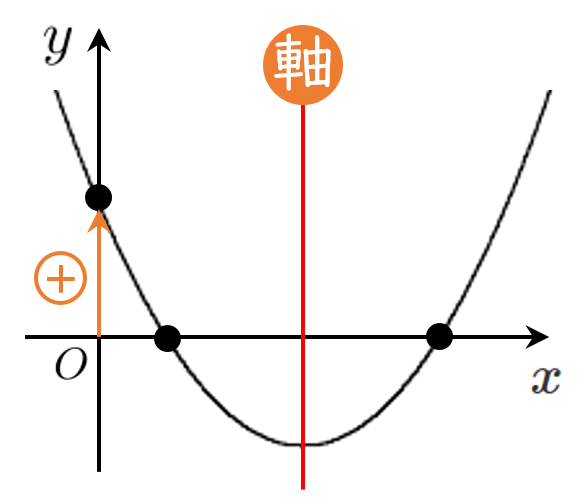
[1] $x$ 軸と異なる2つの共有点をもつ
$f(x)=0$ の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=a^2-(-a+2)=(a-1)(a+2)}$
$D>0$ より $a<-2$,$1<a$ … ①
[2] 軸が $x>0$ の部分にある
$y=f(x)$ の軸は直線 $x=a$ であるから $a>0$ … ②
[3] $x=0$ における $y$ 座標が正
$f(0)>0$ であるから $f(0)=-a+2>0$
よって $a<2$ … ③
①~③の共通範囲をとって $1<a<2$
(2)
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異なる2つの負の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の負の部分と異なる2つの共有点をもつことである
よって,次の [1]~[3] がすべて成り立つ
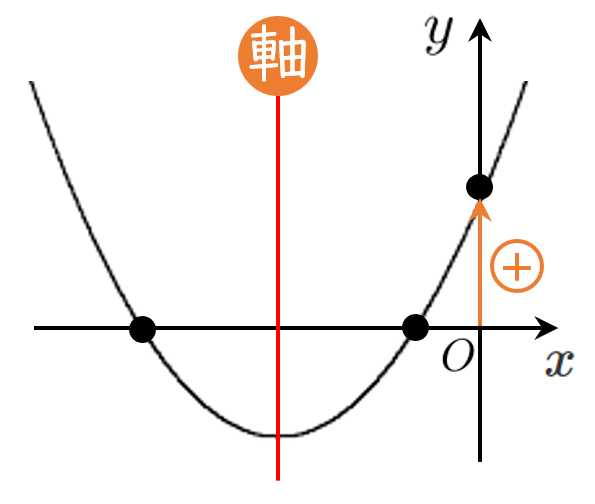
[1] $x$ 軸と異なる2つの共有点をもつ
$f(x)=0$ の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=a^2-(-a+2)=(a-1)(a+2)}$
$D>0$ より $a<-2$,$1<a$ … ①
[2] 軸が $x<0$ の部分にある
$y=f(x)$ の軸は直線 $x=a$ であるから $a<0$ … ②
[3] $x=0$ における $y$ 座標が正
$f(0)>0$ であるから $f(0)=-a+2>0$
よって $a<2$ … ③
①~③の共通範囲をとって $a<-2$
(3)
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異符号の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の正の部分と負の部分で共有点をもつことである
すなわち $x=0$ における $y$ 座標が負
$f(0)<0$ であるから $f(0)=-a+2<0$
よって $a>2$
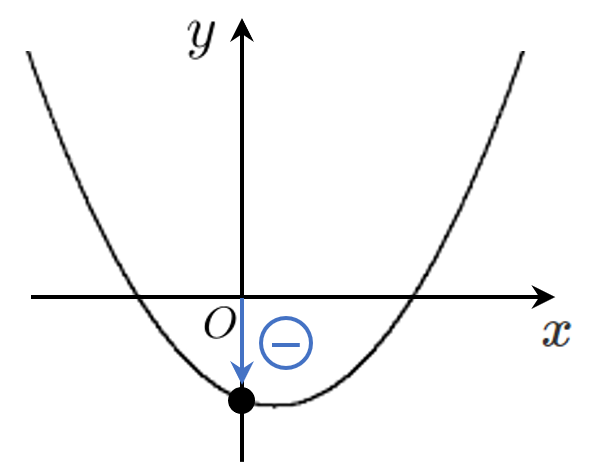
2次方程式が異なる2つの正の解をもつ
2次方程式 $f(x)=0$ が異なる2つの正の解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の正の部分と異なる2つの共有点をもつ
[1] $D>0$ ← $x$ 軸と異なる2つの共有点
[2] 軸 $>0$ ← 軸が $x>0$ の部分にある
[3] $f(0)>0$ ← $x=0$ における $y$ 座標が正
[1]判別式・[2]軸の位置・[3]端点の $y$ 座標に着目する


『判・軸・端』に着目しよう!
(1)
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異なる2つの正の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の正の部分と異なる2つの共有点をもつことである
よって,次の [1]~[3] がすべて成り立つ

[1] $x$ 軸と異なる2つの共有点をもつ(判別式)
$f(x)=0$ の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=a^2-(-a+2)=(a-1)(a+2)}$
$D>0$ より $a<-2$,$1<a$ … ①
[2] 軸が $x>0$ の部分にある(軸の位置)
$y=f(x)$ の軸は直線 $x=a$ であるから $a>0$ … ②
[3] $x=0$ における $y$ 座標が正(端点の $y$ 座標)
$f(0)>0$ であるから $f(0)=-a+2>0$
よって $a<2$ … ③
①~③の共通範囲をとって $1<a<2$
2次方程式が異なる2つの負の解をもつ
2次方程式 $f(x)=0$ が異なる2つの負の解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の負の部分と異なる2つの共有点をもつ
[1] $D>0$ ← $x$ 軸と異なる2つの共有点
[2] 軸 $<0$ ← 軸が $x<0$ の部分にある
[3] $f(0)>0$ ← $x=0$ における $y$ 座標が正
[1]判別式・[2]軸の位置・[3]端点の $y$ 座標に着目する


『異なる2つの正の解をもつ条件』と比べると、
軸の条件が違うだけだね!
(2)
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異なる2つの負の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の負の部分と異なる2つの共有点をもつことである
よって,次の [1]~[3] がすべて成り立つ

[1] $x$ 軸と異なる2つの共有点をもつ(判別式)
$f(x)=0$ の判別式を $D$ とすると
$\displaystyle{\frac{D}{4}=a^2-(-a+2)=(a-1)(a+2)}$
$D>0$ より $a<-2$,$1<a$ … ①
[2] 軸が $x<0$ の部分にある(軸の位置)
$y=f(x)$ の軸は直線 $x=a$ であるから $a<0$ … ②
[3] $x=0$ における $y$ 座標が正(端点の $y$ 座標)
$f(0)>0$ であるから $f(0)=-a+2>0$
よって $a<2$ … ③
①~③の共通範囲をとって $a<-2$
2次方程式が符号の異なる2つの解をもつ
2次方程式 $f(x)=0$ が符号が異なる2つの解をもつ
$\iff$ 2次関数 $y=f(x)$ が $x$ 軸の正の部分と負の部分で共有点をもつ
[3] $f(0)<0$ ← $x=0$ における $y$ 座標が負
端点の $y$ 座標に着目する
※[1] 判別式 と [2] 軸の位置 は必要ない

(3)
$f(x)=x^2-2ax-a+2$ とおくと
方程式 $f(x)=0$ が異符号の解をもつための条件は $y=f(x)$ のグラフが $x$ 軸の正の部分と負の部分で共有点をもつことである
すなわち $x=0$ における $y$ 座標が負(端点の $y$ 座標)
$f(0)<0$ であるから $f(0)=-a+2<0$
よって $a>2$

🔵2次関数のグラフの平行移動・対称移動
🔴軸に定数を含む2次関数の最大・最小の場合分け
🔴定義域の片端に定数を含む2次関数の最大・最小の場合分け
🔴定義域の両端に定数を含む2次関数の最大・最小の場合分け
🔵因数分解形の利用した2次関数の決定
🔴場合分けが必要な文字係数の方程式
🔵2次関数がx軸から切り取る線分の長さ
🔴文字係数の2次不等式
🔴異なる2つの○より大きい・小さい解
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント