直線上の点
直線 $OA$ 上に点 $B$ があるとき,実数 $k$ を用いて
$\overrightarrow{OB}=k\overrightarrow{OA}$
と表すことができる
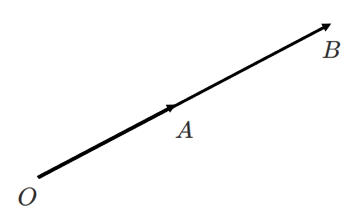
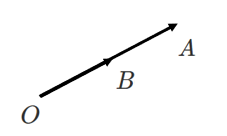
$\overrightarrow{OA}$ を $k$ 倍に拡大または縮小したベクトルが $\overrightarrow{OB}$ なので
$\overrightarrow{OB}=k\overrightarrow{OA}$
平面上の点
平面 $ABC$ 上に点 $P$ があるとき
$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$
を満たす実数 $s$,$t$ が存在する
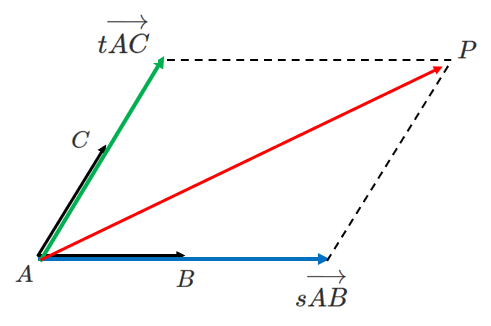
$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$
平面 $ABC$ における点 $A$ を始点とする $\overrightarrow{AB}$,$\overrightarrow{AC}$ を用いると
同じ平面上にある点 $P$ について,$\overrightarrow{AP}$ は
$\overrightarrow{AP}=□\overrightarrow{AB}+□\overrightarrow{AC}$
と1通りに表すことができる
始点を $B$ や $C$ にしてもよい
例えば
$\overrightarrow{CP}=s\overrightarrow{CA}+t\overrightarrow{CB}$
のように表すことができる
詳しくはこれ↓

四面体
四面体 $\cdots\cdots$ $4$ つの三角形でできる立体
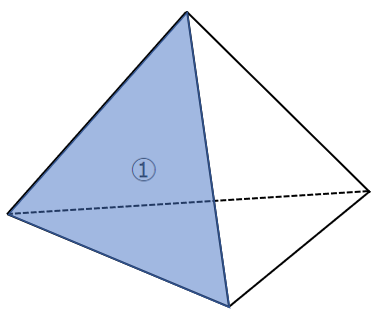
すべての三角形が正三角形の場合は 正四面体

四面体の問題を解く場合は,どこかの三角形に着目して解くことがコツだよ!
直線と平面の交点のベクトル
四面体に関する問題
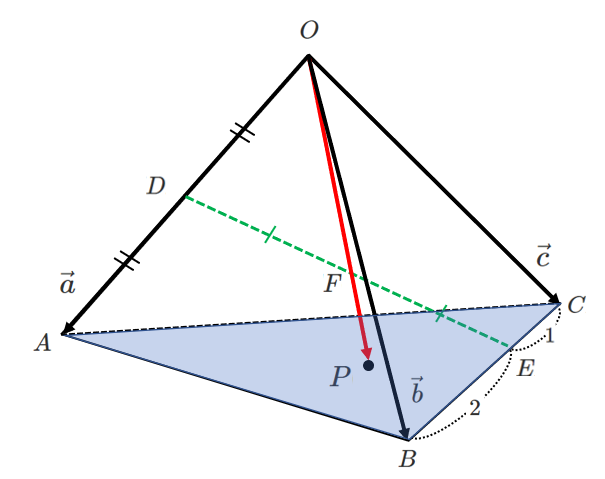
点 $P$ の条件を用いて $\overrightarrow{OP}$ を2通りで表して係数比較
① 点 $P$ は直線 $OF$ 上にある
② 点 $P$ は平面 $ABC$ 上にある

この考え方をおさえて問題を解いてみよう!
点 $P$ は直線 $OF$ 上にあるので,
$\overrightarrow{OP}=k\overrightarrow{OF}$
となる実数 $k$ がある
ここで,
\begin{eqnarray} \overrightarrow{OD} &=& \frac{1}{2}\overrightarrow{OA} \\\\ &=& \frac{1}{2}\vec{a} \end{eqnarray}また,
\begin{eqnarray} \overrightarrow{OE} &=& \frac{\overrightarrow{OB}+2\overrightarrow{OC}}{2+1} \\\\ &=& \frac{1}{3}\vec{b}+\frac{2}{3}\vec{c} \end{eqnarray}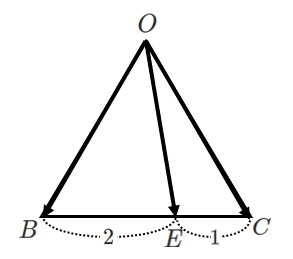
以上より,
\begin{eqnarray} \overrightarrow{OF} &=& \frac{\overrightarrow{OD}+\overrightarrow{OE}}{2} \\\\ &=& \frac{\frac{1}{2}\vec{a}+\frac{1}{3}\vec{b}+\frac{2}{3}\vec{c}}{2} \\\\ &=& \frac{1}{4}\vec{a}+\frac{1}{6}\vec{b}+\frac{1}{3}\vec{c} \end{eqnarray}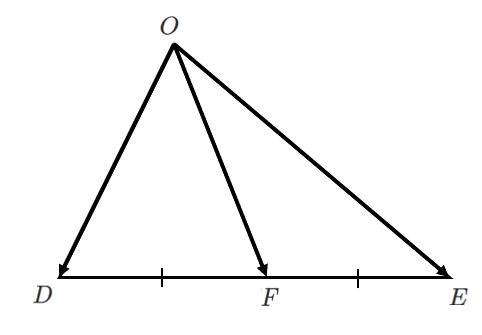
よって,
\begin{eqnarray} \overrightarrow{OP} &=& k\overrightarrow{OF} \\\\ &=& k(\frac{1}{4}\vec{a}+\frac{1}{6}\vec{b}+\frac{1}{3}\vec{c}) \\\\ &=& \frac{1}{4}k\vec{a}+\frac{1}{6}k\vec{b}+\frac{1}{3}k\vec{c} \cdots\cdots ① \end{eqnarray}点 $P$ は平面 $ABC$ 上にあるので,
$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$
となる実数 $s$,$t$ がある
よって,
\begin{eqnarray} \overrightarrow{OP} &=& \overrightarrow{OA}+\overrightarrow{AP} \\\\ &=& \overrightarrow{OA}+s\overrightarrow{AB}+t\overrightarrow{AC} \\\\ &=& \vec{a}+s(\vec{b}-\vec{a})+t(\vec{c}-\vec{a}) \\\\ &=& (1-s-t)\vec{a}+s\vec{b}+t\vec{c} \cdots\cdots ② \end{eqnarray}$\vec{a}$,$\vec{b}$,$\vec{c}$ は1次独立なので,
($O$,$A$,$B$,$C$ は同じ平面上にないので)
$\overrightarrow{OP}$ の表し方はただ1通りである
①,②より
$\displaystyle{\frac{1}{4}k=1-s-t}$, $\displaystyle{\frac{1}{6}k=s}$, $\displaystyle{\frac{1}{3}k=t}$
$\displaystyle{\frac{1}{6}k=s}$, $\displaystyle{\frac{1}{3}k=t}$ を $\displaystyle{\frac{1}{4}k=1-s-t}$ に代入すると
$\displaystyle{\frac{1}{4}k=1-\frac{1}{6}k-\frac{1}{3}k}$
$\displaystyle{k=\frac{4}{3}}$
①に代入すると
$\displaystyle{\overrightarrow{OP}=\frac{1}{3}\vec{a}+ \frac{2}{9}\vec{b}+ \frac{4}{9}\vec{c}}$

平面ベクトルの「2直線の交点におけるベクトル」と似ているね!

これも『求めたいベクトルを2通りで表して係数比較』という解き方だね!
まとめ
● 直線上の点
直線 $OA$ 上に点 $B$ があるとき,実数 $k$ を用いて
$\overrightarrow{OB}=k\overrightarrow{OA}$
と表すことができる
● 平面上の点
平面 $ABC$ 上に点 $P$ があるとき
$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$
を満たす実数 $s$,$t$ が存在する
● 直線と平面の交点におけるベクトル
求めたいベクトルを2通りで表して係数比較して解く

空間のベクトルの分野において,超重要な問題!
しっかり練習してマスターしよう!




コメント