高校数学Ⅱで習う『相加平均と相乗平均の大小関係』をわかりやすく解説しました!
共通テストや個別学力試験に向けて本格的に数学の勉強を進めていくと、よく登場するのが『相加平均と相乗平均の大小関係』です!
『相加平均と相乗平均の大小関係』が使える場面は「逆数どうしの和」がポイント!
証明や最小値を求めるときに利用する方法を解説しています!

「相加平均と相乗平均の大小関係」は,証明に使われるイメージが強いけど,証明以外で使う場面の方が多いよ!
どんなときに使うか確認しよう!
相加平均と相乗平均の基本はこれ↓

相加平均と相乗平均の大小関係
$a>0$,$b>0$ とすると
相加平均が $\displaystyle{\frac{a+b}{2}}$
相乗平均が $\sqrt{ab}$
(相加平均)≧(相乗平均) が成り立つので
$\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$
等号が成り立つのは,$a=b$ のとき
相加平均と相乗平均の大小関係を式変形
$\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$ を式変形すると
$a+b≧2\sqrt{ab}$
この式で用いることが多い
$a>0$,$b>0$ のとき, $a+b≧2\sqrt{ab}$
等号が成り立つのは,$a=b$ のとき
相加平均と相乗平均の大小関係が使える場面

「相加平均と相乗平均の大小関係」は使う場面がよくわからないよ!

多くの高校生が悩んでいることだね!
実を言うと,「相加平均と相乗平均の大小関係」を使う場面はとても分かりやすいよ!
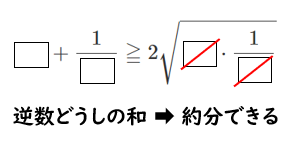
『逆数どうしの和』の例
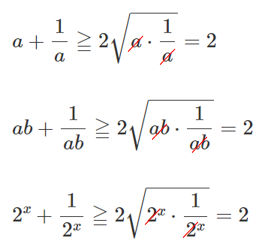
相加平均と相乗平均の大小関係を用いることで、$\displaystyle{2^x+\frac{1}{2^x}≧2}$ であることがわかる。
すなわち、$\displaystyle{2^x+\frac{1}{2^x}}$ が $2$ 以上であることがわかるので、相加平均と相乗平均の大小関係を用いると最小値を求めることができる。
※正確には、等号成立を調べて初めて最小値ということがわかる。

このような『逆数どうしの和』の式が出てきたら,「相加平均と相乗平均の大小関係」を思い出そう!
使う場面①証明
$a>0$,$\displaystyle{\frac{1}{a}>0}$ より,相加平均と相乗平均の大小関係を用いて,
$\displaystyle{a+\frac{1}{a}≧2\sqrt{a\cdot\frac{1}{a}}=2}$ ← $a+b≧2\sqrt{ab}$ を利用
等号が成り立つのは,$\displaystyle{a=\frac{1}{a}}$ のとき途中計算
両辺に $a$ をかけて, $a^2=1$
$a>0$ より, $a=1$
$a>0$ より,$a=1$ のとき
したがって, $\displaystyle{a+\frac{1}{a}≧2}$ が成り立つ
使う場面②最小値
$a>0$,$\displaystyle{\frac{4}{a}>0}$ より,相加平均と相乗平均の大小関係を用いて,
$\displaystyle{a+\frac{4}{a}≧2\sqrt{a\cdot\frac{4}{a}}=4}$ ← $a+b≧2\sqrt{ab}$ を利用
等号が成り立つのは,$\displaystyle{a=\frac{4}{a}}$ のとき途中計算
両辺に $a$ をかけて, $a^2=4$
$a>0$ より,$a=2$
$a>0$ より,$a=2$ のとき
したがって, $\displaystyle{a+\frac{4}{a}}$ は $a=2$ で最小値 $4$
まとめ
● 相加平均と相乗平均の大小関係
$a>0$,$b>0$ のとき $\displaystyle{\frac{a+b}{2}≧\sqrt{ab}}$
等号が成り立つのは,$a=b$ のとき
実際には,式変形した $a+b≧2\sqrt{ab}$ を用いる
● 相加平均と相乗平均の大小関係を使う場面
『逆数どうしの和』があるとき
例 $\displaystyle{a+\frac{1}{a}}$
$\displaystyle{ab+\frac{1}{ab}}$
$\displaystyle{2^x+\frac{1}{2^x}}$
問題
(1) $\displaystyle{4a+\frac{1}{a}}$
(2) $\displaystyle{2^x+\frac{1}{2^x}}$
(1) $\displaystyle{4a+\frac{1}{a}}$
$4a>0$,$\displaystyle{\frac{1}{a}>0}$ より,相加平均と相乗平均の大小関係を用いて,
$\displaystyle{4a+\frac{1}{a}≧2\sqrt{4a\cdot\frac{1}{a}}=4}$
等号が成り立つのは,$\displaystyle{4a=\frac{1}{a}}$ のとき途中計算
両辺に $a$ をかけて, $\displaystyle{a^2=\frac{1}{4}}$
$a>0$ より, $\displaystyle{a=\frac{1}{2}}$
$a>0$ より,$\displaystyle{a=\frac{1}{2}}$ のとき
したがって, $\displaystyle{4a+\frac{1}{a}}$ は $\displaystyle{a=\frac{1}{2}}$ で最小値 $4$
(2) $\displaystyle{2^x+\frac{1}{2^x}}$
$2^x>0$,$\displaystyle{\frac{1}{2^x}>0}$ より,相加平均と相乗平均の大小関係を用いて,
$\displaystyle{2^x+\frac{1}{2^x}≧2\sqrt{2^x\cdot\frac{1}{2^x}}=2}$
等号が成り立つのは,$\displaystyle{2^x=\frac{1}{2^x}}$ のとき途中計算
両辺に $2^x$ をかけて, $2^{2x}=1$
$x=0$
すなわち,$x=0$ のとき
したがって, $\displaystyle{2^x+\frac{1}{2^x}}$ は $x=0$ で最小値 $2$

『逆数どうしの和』を見つけたら「相加平均と相乗平均の大小関係」を思い出そう!




コメント