
空間のベクトルを考える上で必要な空間の点について考えよう!
平面の点

今まで考えていたのは「平面」の点!
$x$ 軸と $y$ 軸をとって考えることができる!
点の位置を考えるために以下のように座標を使う
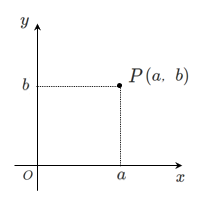

平面のことを $2$ 次元といったりするね!
空間の座標軸と座標平面

平面を拡張して空間の点について学ぼう!
$x$ 軸,$y$ 軸に加えて $z$ 軸をとると空間の点を考えることができるよ!

どこに $z$ 軸をとればいいの?

原点を通って,$x$ 軸と $y$ 軸で作られる平面に垂直にとればいいよ!
簡単にいうと,ペンを原点のところに垂直に立てると $z$ 軸になるよ!
空間に点 $O$ をとり,点 $O$ で互いに直交する $3$ 本の数直線を下の図のように定める。
これらをそれぞれ $x$ 軸,$y$ 軸,$z$ 軸といい,まとめて 座標軸 という。
また,点 $O$ を原点という。
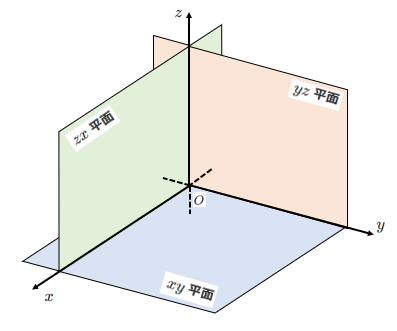
$x$ 軸と $y$ 軸で定まる平面を $xy$ 平面
$y$ 軸と $z$ 軸で定まる平面を $yz$ 平面
$z$ 軸と $x$ 軸で定まる平面を $zx$ 平面
これらをまとめて 座標平面 という。
空間の座標

空間の座標の取り方を学ぼう!
平面と同様に $P(1,3,2)$ について,左から順に
点 $P$ の $x$ 座標,$y$ 座標,$z$ 座標
という
途中までは平面と同じで $(1,3)$
空間の座標の表し方をすると,$(1,3,0)$ をとる
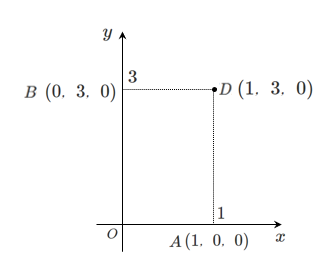
空間でみると
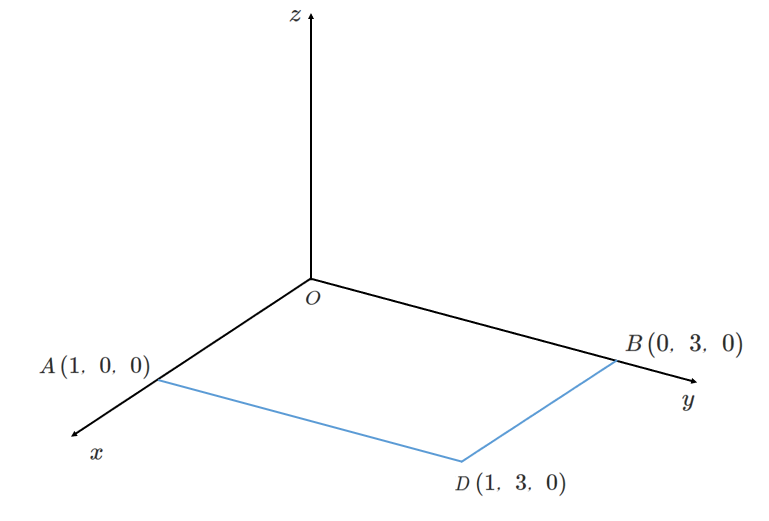
点 $D$ から $z$ 軸方向に $2$ だけ移動した点が $P(1,3,2)$
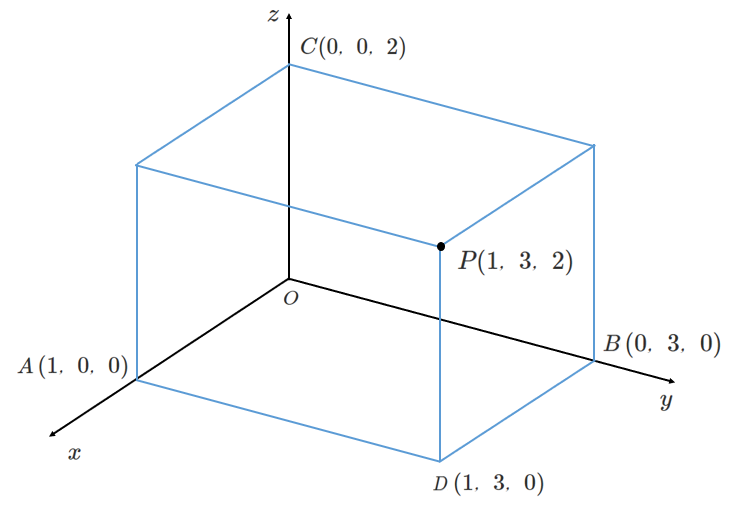
以上をまとめると次のようになる
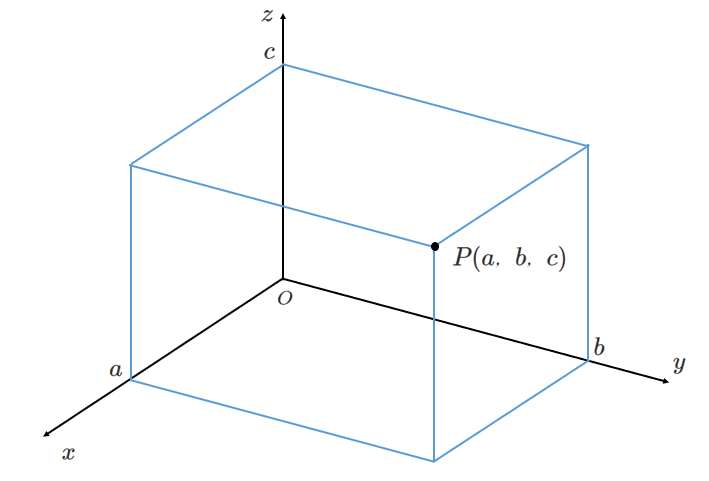
座標の定められた空間を 座標空間 という
原点 $O$ の点 $P$ の距離

空間の点の距離の考え方を学ぼう!
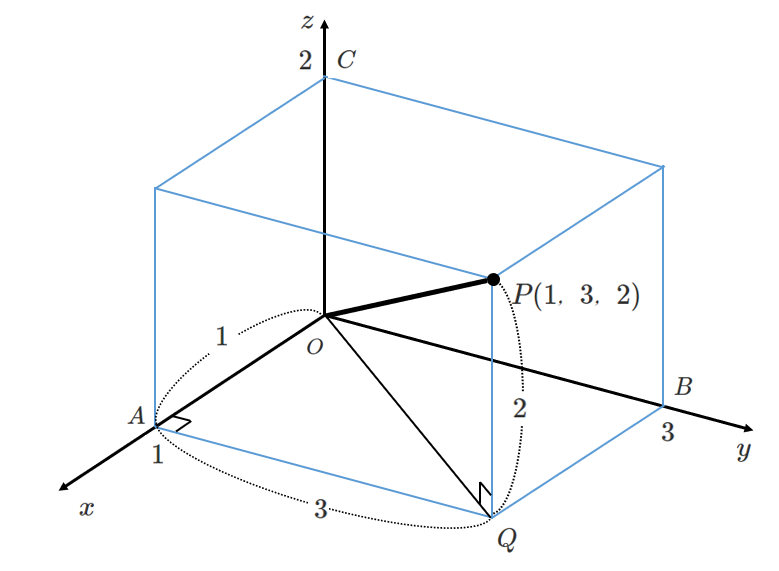
$\triangle OAQ$ において三平方の定理を用いると
$OQ^2=OA^2+AQ^2$ $\cdots\cdots$ ①
$\triangle OPQ$ において三平方の定理を用いると
$OQ^2=OQ^2+PQ^2$ $\cdots\cdots$ ②
①を②に代入すると
\begin{eqnarray} OP^2 &=& OQ^2+PQ^2 \\\\ &=& (OA^2+AQ^2)+PQ^2 \\\\ &=& 1^2+3^2+2^2 \\\\ &=& 14 \end{eqnarray}$OP>0$ より
$OP=\sqrt{14}$
原点と点 $P(a,b,c)$ の距離 $OP$ を考えると
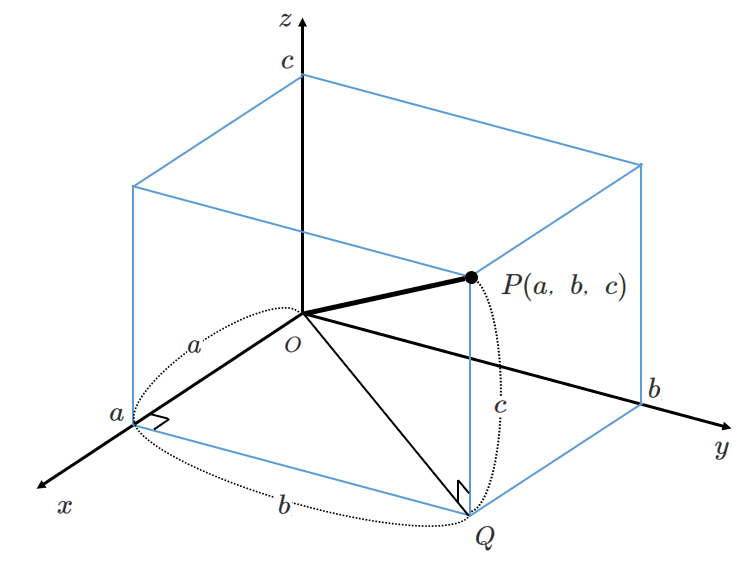
$OP>0$ より
$OP=\sqrt{a^2+b^2+c^2}$
$OP=\sqrt{a^2+b^2+c^2}$

平面上の点の距離と似ているね!
問題を解いてみよう!
原点 $O$ と次の点の距離を求めよ。
(1) $P(2,3,4)$
(2) $P(-2,1,-4)$
(1) $P(2,3,4)$
\begin{eqnarray} OP &=& \sqrt{2^2+3^2+4^2} \\\\ &=& \sqrt{29} \end{eqnarray}
(2) $P(-2,1,-4)$
\begin{eqnarray} OP &=& \sqrt{(-2)^2+1^2+(-4)^2} \\\\ &=& \sqrt{21} \end{eqnarray}
まとめ
● 空間の点の座標

● 空間の点の距離
原点 $O$ と点 $P(a,b,c)$ の距離は
$OP=\sqrt{a^2+b^2+c^2}$


空間の点の基本をおさえよう!




コメント